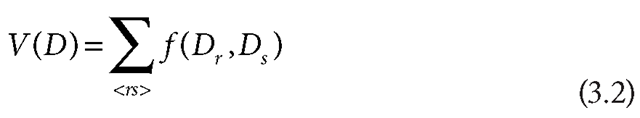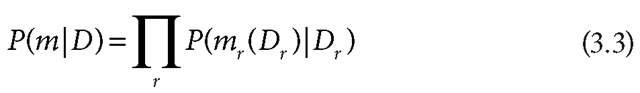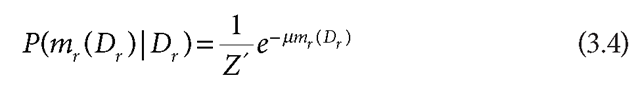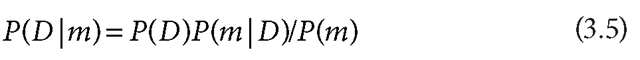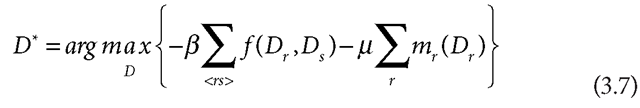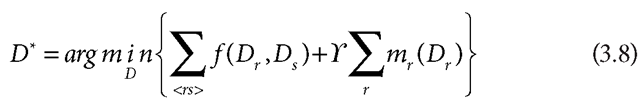Introduction
Bayesian and other related statistical techniques have emerged as a dominant paradigm in computer vision for estimating three-dimensional (3D) surfaces in the presence of noisy and sparse depth cues. In particular, for 3D reconstruction problems, these techniques have been implemented using Markov random fields (MRFs), which are probabilistic models that express how variables arranged in a spatial structure jointly vary, such as a rectangular grid of disparity variables aligned to a pixel lattice in a stereo model. Such MRF models incorporate powerful priors on surface geometry, which allow 3D estimates to combine evidence from depth cues with prior knowledge of smoothness constraints. They embody a natural mechanism for propagating surface information from regions with highly informative depth cues to neighboring regions with unreliable or missing depth cues, without crossing over depth discontinuities. Recent advances in inference algorithms have enlarged the range of statistical models that are tractable for computer implementation, enabling the use of increasingly realistic and expressive models and leading to some of the most robust and accurate 3D estimation algorithms to date. Finally, a “belief propagation” framework allows these models to be implemented on a massively parallel computer architecture, raising the possibility that they may be realized in a biologically plausible form.
3D reconstruction is a major theme in computer vision, with techniques for estimating shape from a variety of cues, including shading (Haines and Wilson, 2008), texture (White and Forsyth, 2006), and multiview stereo (Seitz, Curless, Diebel, Scharstein, and Szeliski, 2006). A fundamental challenge of 3D reconstruction is estimating depth information everywhere in a scene despite the fact that depth cues are noisy and sparse. These properties of depth cues mean that depth information must be propagated from regions of greater certainty to regions of lesser certainty. The 3D reconstruction problem that is perhaps the most mature in computer vision is stereo using two or more calibrated cameras with known epipolar geometry. The most successful stereo algorithms use MRFs (Chellappa and Jain, 1993), which are probabilistic models that express the joint distribution of variables arranged in a network structure, with the state of any variable exerting a direct influence on the states of its neighbors. In the case of stereo (here we consider two-view stereo), a basic MRF model consists of a lattice (grid) of disparity variables, one for each pixel in the image. For any disparity hypothesized at a given pixel, there is (usually ambiguous) evidence from the corresponding match between the left and right images that this disparity implies. Nearest-neighbor connections enforce a prior smoothness constraint on disparities, which equates to a related smoothness constraint on depths in the scene. Inference is performed using a global optimization method such as graph cuts (Boykov, Veksler, and Zabih, 2001) or belief propagation (Yedidia, Freeman, and Weiss, 2001), which determines a near-optimal assignment of disparities to each pixel given the image data. The MRF framework embodies a natural mechanism for propagating surface information in the presence of noisy and sparse data.
This topic is intended to present the basic principles of this framework (which generalize to any 3D reconstruction problem, not just two-frame stereo) to an audience of vision researchers who are not computer vision specialists. I discuss recent extensions incorporating more realistic modeling of surface geometry, and point to recent work suggesting the possibility that belief propagation (or something close to it) may be realized in a biologically plausible form. Finally, I suggest possible directions for future research.
Markov random fields For Stereo
In this section, we outline a simple MRF (Markov random field) formulation of stereo, which we describe using a Bayesian model. (Other statistical variants such as conditional random fields (Lafferty, McCallum, and Pereira, 2001; Scharstein and Pal, 2005), which we mention below, are popular alternatives that are similar.) We are given two grayscale images L and R (left and right), which are assumed rectified so that a pixel in one image is guaranteed to match a pixel in the same row in the other image. The unknown disparity field is represented by D, with Dr representing the disparity at pixel location r. A particular disparity value Dr , where r = (x, y), has the following interpretation: (x + Dr, y) in the left image corresponds to (x, y) in the right image.
We define a prior on the disparity field D that enforces smoothness:
where Z is a normalizing constant ensuring that P(D) sums to 1 over all possible values of D, ß is a positive constant that controls the peakedness of the probability distribution (which in turn determines the importance of the prior relative to the likelihood, discussed below), and
where the sum is over all neighboring pairs of pixels r and 5. Here, f (Dr, Ds ) is an energy function that penalizes differences between disparities in neighboring pixels, with higher energy values corresponding to more severe penalties. (In other words, nonzero values of the first derivative of the disparity field in the x and y directions are penalized.) One possible choice for the function is f (Dr, Ds ) = |Dr – Ds|. A popular variation (Zhang and Seitz, 2005) is f (Dr,Ds ) = (|Dr -Ds|,t), which ensures that the penalty can be no larger than ; this is appropriate in scenes with depth discontinuities, where a large difference between disparities on either side of a depth edge may be no less probable than a moderate difference.
Note that a prior of this form enforces a bias toward fronto-parallel surfaces, over which the disparity is constant; we will discuss ways of relaxing this bias later.
Next, we define a likelihood function, which defines how the left and right images provide evidence supporting particular disparity values:
where the product is over all pixels in the image, and m is the matching error across the entire image. Specifically, mr(Dr ) is the matching error between the left and right images assuming disparity Dr defined as mr (Dr ) = |L(x + Dr,y) – R(x,y)| (again r = (x,y)). (The product form assumes that the matching errors are conditionally independent given the disparity field.) A simple model for the matching error is given by
which assigns a higher penalty (lower probability) to higher matching errors.
The Bayesian formulation defines a posterior distribution of disparities given both images, given by the Bayes theorem:
To perform inference with the model, one typically finds the maximum a posterior (MAP) estimate of the disparity field (i.e., the value of D that maximizes the posterior).
Note that because P(m) is independent of D, we can write the MAP estimate of D, denoted D*, as
Because maximizing any function is equivalent to maximizing the log of the function, we can reexpress this as
where we have removed constants independent of D such as Z and Z’. This is equivalent to
where Y = ß/ß expresses the relative weight of the prior and likelihood energies.
We discuss methods for estimating the MAP in the next section. Model Improvements and Refinements
We note that this MRF is a particularly simple model of stereo, and that many improvements and refinements are commonly added, such as the following:
1. Considerable performance improvements have been attained by exploiting the tendency for disparity discontinuities to be accompanied by intensity edges (Scharstein and Pal, 2005). To accomplish this, the disparity smoothness function is modulated by a measure of the image gradient, so that large disparity differences between neighboring pixels are penalized less severely when there is a strong intensity difference between the pixels. (Alternatively, a general-purpose monocular segmentation algorithm may be run to determine the likely locations of edges between regions of different intensity or color, instead of relying on a purely local measure of the image gradient.) Thus, surface information is naturally propagated from regions with highly informative depth cues to neighboring regions with unreliable or missing depth cues, without crossing over depth discontinuities.
2. The matching function used in the likelihood model can be based on comparisons of image properties that are richer than grayscale intensity—for example, full red, blue, green (RGB) color, intensity gradient (magnitude and direction), or higher-level descriptors incorporating neighboring image structure (such as DAISY) (Tola, Lepetit, and Fua, 2008).
3. MRF models may be multiscale (Felzenszwalb and Huttenlocher, 2006), with a pyramid structure coupling the original disparity lattice with subsampled (coarsened) versions of it.
4. The conditional independence assumption in Equation (3.3) can be relaxed with the use of conditional random fields, resulting in a more realistic posterior distribution.
How MRFs Propagate Information
We now briefly explain how the MRF model propagates noisy and sparse disparity cues throughout the image. The general principle behind this process is that the prior and likelihood distributions compete for various disparity hypotheses, and the relative strength of these two sources of information automatically varies across the image according to which source is more reliable.
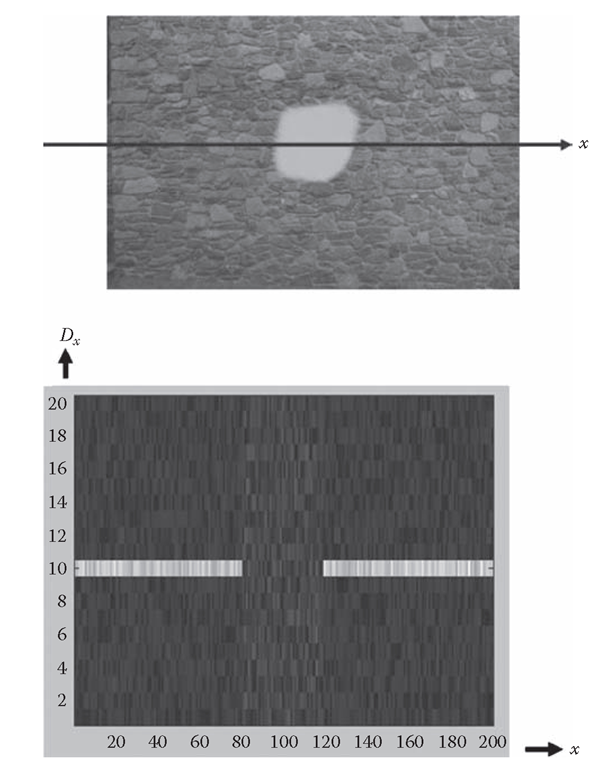
In Figure 3.1 we show a simple example of a scene consisting only of a flat surface oriented fronto-parallel to the cameras (so that the correct disparity field is uniform across the image, with value do). The entire surface contains a highly textured, nonperiodic pattern, except for a central region that is textureless. Everywhere in the textured part of the image, the likelihood model provides strong evidence for the correct disparity do and very low evidence for anything but do (in practice, the likelihood model will be less discriminating, but we assume near-perfect disparity discrimination for the sake of argument). By contrast, in the central region there will be no direct evidence favoring one disparity over another. Any attempt to perform inference using the likelihood without the prior will obviously fail in the central region. However, by incorporating the prior with the likelihood, it is easy to see that a disparity field that has a uniform value of do over the entire image will have a higher posterior probability than any other possible disparity field, because any disparity field that deviates from do will be less smooth than the correct disparity field (while having the same support from the likelihood model).
More realistic examples can be analyzed exhibiting similar behavior, in which the MRF prior model propagates surface information even when the disparity cues are noisy or nonexistent.
FIGURE 3.1 Idealized example of how disparity information is propagated across an image. Top: image of a fronto-parallel surface (stone wall), with x-axis slice superimposed on the image. Bottom: support for different disparities Dx for all possible values of x, with brightness proportional to degree of support. In textured parts of a slice, the disparity value d0 = 10 is strongly supported; in the textureless part of slice toward the center, all disparity values have approximately equal support. See text for explanation of how MRF model propagates d0 = 10 solution across the untextured region.
Tractable Inference and Learning
A significant challenge posed by the stereo MRF model (and many other Bayesian models) is the difficulty in estimating the MAP, which is equivalent to minimizing the energy function in Equation (3.8). There are no techniques that are guaranteed to find the exact MAP in general cases, aside from an exhaustive search, which is impractical (e.g., SN possible disparity fields must be evaluated, where typical values are S = 50 for the number of possible disparities and N = 10,000 for the number of pixels in the image). Typical energy minimization techniques such as gradient descent (Gershenfeld, 1998) work well only when the energy function has one dominant, global minimum. However, the type of energy function defined by Equation (3.8) has a much more irregularly shaped energy landscape, with many local minima, and gradient descent-type techniques will typically converge to a local minimum that is far from the global minimum.
A variety of approximation techniques are available for estimating the MAP. Until fairly recently, one of the best available techniques was simulated annealing (Gershenfeld, 1998), which is essentially a form of a gradient descent perturbed by stochastic noise. While simulated annealing can succeed in locating a “good” local minimum (if not the global minimum), it is an extremely slow technique. In fact, its slowness meant that most MRF models in computer vision were extremely difficult to use, and as a result, progress in MRF model development was hindered.
However, approximately 10 years ago, two efficient energy minimization techniques were introduced to computer vision (imported from other fields), graph cuts (Boykov, Veksler, and Zabih, 2001), and belief propagation (Yedidia, Freeman, and Weiss, 2001). Both energy minimization techniques find approximate solutions in general, attaining exact solutions in only certain special cases. Even though both techniques are popular in a variety of computer vision MRF models, we will only discuss belief propagation (BP), which is more intuitive than graph cuts (and perhaps more related to biologically plausible mechanisms) and will provide additional insight into how MRFs propagate information. (The techniques perform minimization of energy functions with discrete variables, which means that the disparity values must be quantized into a finite set of values, for example, integer pixel values or subpixel values within a finite range.)
BP is a fast, iterative procedure for estimating the minimum energy (maximum probability) joint configuration of all the variables in an MRF (i.e., the joint estimate of the most likely states of all the variables). (It is also used to solve the related problem of estimating marginal probabilities of individual variables, which specify the probabilities of all possible states for each variable.) The main idea behind BP is that neighboring variables “talk” to each other at each iteration, with each variable passing “messages” to its neighbors with their estimates of the neighbors’ likely states.
After enough iterations, this series of “conversations” is likely to converge to a consensus specifying which state is most likely for each variable.
The messages exchanged between variables in BP pass information throughout the MRF. Information can only be passed from variables to their immediate neighbors in one iteration of BP, but after enough iterations, it is possible for information to be passed between all variables. At the start of BP, messages express no preference for one state over another, but after enough iterations, the messages become more “opinionated,” expressing strong preferences for certain states.
Finally, we note that stereo inference using BP (or graph cuts) is still slow relative to simpler (but less accurate) stereo algorithms, requiring on the order of seconds (or even minutes) for each pair of images. However, ongoing work on boosting the efficiency of these algorithms, as well as steadily improving computer hardware, is continually increasing execution speed.