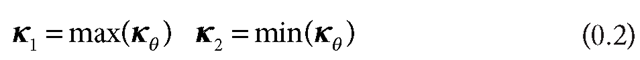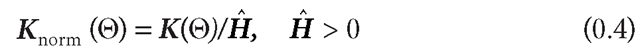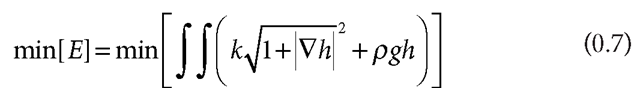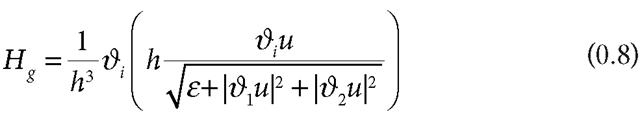Visual Encoding
The primary goal of visual encoding is to determine the nature and motion of the objects in the surrounding environment. In order to plan and coordinate actions, we need a functional representation of the dynamics of the scene layout and of the spatial configuration and the dynamics of the objects within it. The properties of the visual array, however, have a metric structure entirely different from that of the spatial configuration of the objects. Physically, objects consist of aggregates of particles that cohere together. Objects may be rigid or flexible but, in either case, an invariant set of particles is connected to form a given object.
Although the objects may be stable and invariant in the scene before us, the cues that convey the presence of the objects to the eyes are much less stable. They may change in luminance or color, they may be disrupted by reflections or highlights or occlusion by intervening objects. The various cues carrying the information about the physical object structure, such as edge structure, binocular disparity, color, shading, texture, and motion vector fields, typically carry information that is inconsistent. Many of these cues may be sparse, with missing information about the object structure across gaps where there are no edge or texture cues to carry information about the object shape (see Figure 0.1).
FIGURE 0.1 Example of a scene with many objects viewed at oblique angles, requiring advanced three-dimensional surface reconstruction for a proper understanding of the object structure. Although the objects are well-defined by luminance and color transitions, many of the objects have minimal surface texture between the edges. The object shape cannot be determined from the two-dimensional shape of the outline. The three-dimensional structure of the objects requires interpolation from sparse depth cues across regions with no shape information.
The typical approach to computational object understanding is to derive the shape from the two-dimensional (2D) outline of the objects. For complex object structures, however, object shape cannot be determined from the 2D shape of the outline. In the scene depicted in Figure 0.1, many of the objects have nontraditional shapes that have minimal surface texture between the edges and are set at oblique angles to the camera plane. Although the structural edges are well-defined by luminance and color transitions, there are shadows that have to be understood as nonstructural edges, and the structural edges have to be encoded in terms of their three-dimensional (3D) spatial configuration, not just their 2D location. In natural scenes, the 3D information is provided by stereoscopic disparity, linear perspective, motion parallax, and other cues. In the 2D representation of Figure 1, of course, only linear perspective is available, and in a rather limited fashion in the absence of line or grid texture on the surfaces.
Consequently, the 3D structure of the objects requires both
1. Global integration among the various edge cues to derive the best estimate of the edge structure in 3D space, and
2. 3D interpolation from sparse depth cues across regions with no shape information
These are challenging tasks involving an explicit 3D representation of the visual scene, which have not been addressed to be either computational techniques or empirical studies of how the visual system achieves them.
Thus, a primary requirement of neural or computational representations of the structure of objects is the filling-in of details of the threedimensional object structure across regions of missing or discrepant information in the local visual cues. Generating such three-dimensional representations is a fundamental role of the posterior brain regions, but the cortical architecture for the joint processing of multiple depth cues is poorly understood in the brain, especially in terms of the joint processing of diverse visual cues. Computational approaches to the issue of the structure of objects tend to take either a low-level or a high-level approach to the problem. Low-level approaches begin with local feature recognition and an attempt to build up the object representation by hierarchical convergence, using primarily feedforward logic with some recurrent feedback tuning of the results (Marr, 1982; Grossberg, Kuhlmann, and Mingolla, 2007). High-level, or Bayesian, approaches begin with the vocabulary of likely object structures and look for evidence in the visual array as to which object might be there (Huang and Russell, 1998; Rue and Hurn, 1999; Moghaddam, 2001; Stormont, 2007). Both approaches work much better for objects with a stable 2D structure (when translating through the visual scene) than for manipulation of objects with a full 3D structure, such as those in Figure 1, or for locomotion through a complex 3D scene.
Surfaces as a Mid-level Invariant in visual encoding
A more fruitful approach to the issue of 3D object structure is to focus the analysis on midlevel invariants to the object structure, such as surfaces, symmetry, rigidity, texture invariants, or surface reflectance properties.
Each of these properties is invariant under transformations of 3D pose, viewpoint, illumination level, haze contrast, and other variations of environmental conditions. In mathematical terminology, given a set of object points X with an equivalence relation A ~ A’ on it, any function f : X ^ Y is constant over the equivalence classes of the transformations. Various computational analyses have incorporated such invariants in their object-recognition schemes, but a neglected aspect of midlevel vision is the 3D surface structure that is an inescapable property of objects in the world. The primary topic of this topic is therefore to focus attention on this important midlevel invariant of object representation, both to determine its role in human vision and to analyze the potential of surface structure as a computational representation to improve the capability of decoding the object structure of the environment.
Surfaces are a key property of our interaction with objects in the world. It is very unusual to experience objects, either tactilely or visually, except through their surfaces. Even transparent objects are experienced in relation to their surfaces, with the material between the surfaces being invisible by virtue of the transparency. The difference between transparent and opaque surfaces is that only the near surfaces of opaque objects are visible, while in transparent objects both the near and far surfaces are visible. (Only translucent objects are experienced in an interior sense, as the light passes through them to illuminate the density of the material. Nevertheless, the interior is featureless and has no appreciable shape information.) Thus, the surfaces predominate for virtually all objects. Developing a means of representing the proliferation of surfaces before us is therefore a key stage in the processing of objects.
For planar surfaces, extended cues such as luminance shading, linear perspective, aspect ratio of square or round objects, and texture gradient can each specify the slant of a planar surface (see Figure 0.2). Zimmerman, Legge, and Cavanagh (1995) performed experiments to measure the accuracy of surface slant from judgments of the relative lengths of a pair of orthogonal lines embedded in one surface of a full visual scene. Slant judgments are accurate to within 3° for all three cue types, with no evidence of the recession to the frontal plane expected if the pictorial surface was contaminating the estimations. Depth estimates of disconnected surfaces were, however, strongly compressed. Such results emphasize the key role of surface reconstruction in human depth estimation.
In assessing the placement of surfaces in space, Alhazen, in his Optics (AD ~1000), argued that “sight does not perceive the magnitudes of distances of visible objects from itself unless these distances extend along a series of continuous bodies, and unless sight perceives those bodies and their magnitudes” (Sabra, 1989, 155).
FIGURE 0.2 Scene in which texture gradients help to determine the shapes of the objects.
He supported his argument with examples in which the distances are correctly estimated for objects seen resting on a continuous ground, and misperceived as close to each other when the view of the ground is obstructed. Alhazen’s explanation of distance perception was arrived at independently by Gibson (1950), who called it the “ground theory” of space perception, based on the same idea that the visual system uses the ground surface as a reference frame for coding location in space. The orientation of the ground plane relative to the observer is not a given, but it has to be derived from stereoscopic, perspective, and texture gradient cues. Once established, it can form a basis not only for distance estimation but for estimation of the relative orientation of other surfaces in the scene.
The Analysis of Surface Curvature
When surfaces are completed in three dimensions, not just in two dimensions, the defining property is the curvature at each point in the surface. Curvature is a subtle property defined in many ways, but the three most notable properties of surface curvature are its local curvature k, its mean curvature H, and its Gaussian curvature K. These quantities are all continuous properties of the surface.
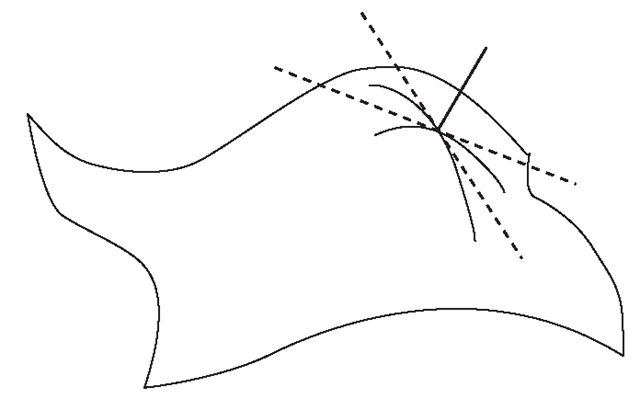
At each point in the surface, a one-dimensional (1D) cut through the surface defines the local curvature k (see Figure 0.3), which is most easily conceptualized as the reciprocal of the radius of curvature for the circle tangent to the curve of the surface at this point. For a cut at some angle 6 in the tangent plane:
As 6 rotates around the point, it describes a curvature function for the surface. Any point on a smooth surface has only one maximum and one minimum direction of curvature, and the directions of maximum and minimum curvature are always at right angles to each other in the tangent plane. Gauss defined these extrema as the principal curvatures for that point in the surface:
where
The principal curvatures at every point are the fundamental intrinsic properties of the surface. The intrinsic 2D curvature is now known as the Gaussian curvature, K, given by the product of the two principal curvatures:
Figure 0.3 Surface curvature. At a local point on any surface, there are orthogonal maximum and minimum curvatures whose tangents (dashed lines) define a local coordinate frame on which the surface normal (thick line) is erected.
If a surface is intrinsically flat, like a sheet of paper, it can never be curved to a form with intrinsic curvature, such as the surface of a sphere. Even if the flat sheet is curved to give the curvature in one direction a positive value, the curvature in the other (minimal) direction will be zero (like a cylinder). Hence, the product forming the Gaussian curvature (Equation 0.3) will remain zero. For any point of a sphere (or any other convex form), however, both the maximum and the minimum curvatures will have the same sign, and K will be positive everywhere on the surface.
When Gaussian curvature is applied to objects, one issue that arises is that the value of K varies as an object changes in size. As a measure of shape, this is an undesirable property, because we think of a sphere, for example, as having the same shape regardless of its size. One option that may be suggested to overcome this problem is to normalize the local Gaussian curvature K to the global mean curvature of the surface of an object H (see Equation 0.4) to provide a measure of the normalized Gaussian curvature Knorm. Objects meaningfully exist only when the mean curvature H > 0, so this should be considered as a restriction on the concept of normalized Gaussian curvature (i.e., an isolated patch of surface with H <= 0) is solely a mathematical construct that cannot be a real object). Normalized Gaussian curvature is thus expressed in polar angle coordinates with respect to the center of the object, 0, and is defined as
where the mean curvature H = (k1 +k2)/2, and global mean curvature is the integral of the local mean curvature over all angles with respect to its center H = JH d0 .
Thus, Knorm = 1 for spheres of all radii, rather than varying with radius as does K, forming a map in spherical coordinates that effectively encodes the shape of the object with a function that is independent of its size. Regions where the local Gaussian curvature matches the global mean Gaussian curvature will have Knorm = 1, and regions that are flat like the facets of a crystal will have Knorm = 0, with high values where they transition from one facet to the next.
Another shape property of interest is mean curvature, defined as the mean of the two principal curvatures. Constant mean curvature specifies a class of surfaces in which H is constant everywhere. In the limiting case, the mean curvature is zero everywhere, H = 0. This is the tendency exhibited by surfaces governed by the self-organizing principle of molecular surface tension, like soap films. The surface tension within the film operates to minimize the curvature of the surface in a manner that is defined by the perimeter to which the soap bubble clings. In principle, the shapes adopted by soap films on a wire frame are minimal surfaces. Note that if H = 0, then k =-k2 and the Gaussian curvature product is negative (or zero) throughout. Thus, minimal surfaces always have negative Gaussian curvature, meaning that they are locally saddle shaped with no rounded bulges or dimples of positive curvature. The surface tension principle operates to flatten any regions of net positive curvature until the mean curvature is zero.
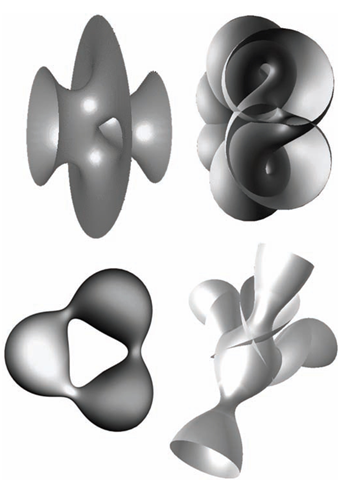
Until 1967, it was thought that there were only two minimal surfaces exhibiting the property of H = 0, the negative-curvature hypersphere and the imaginary-curvature hyperboloid. Since that time, a large class of such surfaces has been discovered. These are very interesting surfaces with quasibiological resonances, suggesting that the minimal surface principle is commonly adopted (or approximated) in biological systems (Figure 0.4). Thus, the simple specification of H = 0 generates a universe of interesting surface forms that may be of relevance in neural processing as much as they are in biological form. The ubiquitous operation of lateral inhibition at all levels in the nervous system is a minimal principle comparable with surface tension. It is generally viewed as operating on a 2D function of the neural array in some tissue such as the retina or visual cortex. However, for any form of neural connectivity that is effectively 3D, lateral inhibition may well operate to form minimal surfaces of neural connectivity with conforming mathematical minimal surface principle (or its dynamic manifestation).
A similar approach to this minimization for the 1D case over the domain r(x) has been proposed by Nitzberg, Mumford, and Shiota (1993) as minima of the elastic functional on the curvature k:
where v and a are constants.
Using a sparse set of depth cues O, one may define a function f : R3 R that estimates the signed geometric distance to the unknown surface S, and then use a contouring algorithm to extract the surface function approximating its zero set:
To make the problem computationally tractable (and a realistic model for neural representation within a 2D cortical sheet), we may propose a restriction to depth in the egocentric direction relative to the 2D array of the visual field, such that the surface is described by the function S(x,y).
FIGURE 0.4 Examples of mathematical minimal surfaces.
This 2D case may be approached through the self-organizing principle that determines the shape of the soap-film surface is the minimization of the energy function defined according to
where h is the height of the surface relative to a coordinate frame, p is the mass density per unit area, and g is the gravitational force acceleration on the soap film.
These formulations, in terms of energy minimization, may provide the basis for the kind of optimization process that needs to be implemented in the neural processing network for the midlevel representation of the arbitrary object surfaces that are encountered in the visual scene. In the neural application, the constant g can be a generalized to a 2D function that takes the role of the biasing effect of the distance cues that drive the minimization to match the form of the object surface.
Another approach to this surface estimation is through the evolution of Riemannian curvature flow (Sarti, Malladi, and Sethian, 2000):
where u(x,y) is the image function, and h is an edge indicator function for the bounding edges of the object.
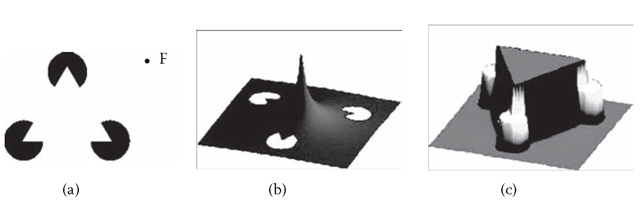
The feasibility of a surface reconstruction process being capable of generating accurate depth structure underlying the subjective contour generation is illustrated for the classic Kanizsa figure (Figure 0.5a) in the computational technique of Sarti, Malladi, and Sethian (2000). As shown in Figure 0.5b, the edge-attractant properties of the Kanizsa corners progressively convert the initial state of the implied surface into a convincing triangular mesa with sharp edges, specifying the depth map of the perceptual interpretation of the triangle in front of the pacmen disk segments. The resulting subjective surface is developed as a minimal surface with respect to distortions induced by the features in the image (Figure 0.5c). This computational morphogenesis of the surface reveals how the interactions within a continuous neural network could operate to generate the sharp subjective contours in the course of the 3D reconstruction of surfaces in the world.
Each of these methods incorporates some level of Bayesian inference as to the probable parameters of surface structure, but such inference may be applied with specific reference to the assessed probabilities of surfaces in the environment (Sullivan et al., 2001; Lee and Mumford, 2003; Yang and Purves, 2003). One goal of the topic is to focus attention on such principles for the analysis of the properties of neural encoding of surfaces, or for the neural encoding of other features of the visual world that involve surface principles in their encoding structure.
FIGURE 0.5 (a) The original Kanizsa (1976) illusory triangle. Importantly, no subjective contours are seen if the white region appears flat. Note also that the illusion disappears with fixation at point F to project the triangle to peripheral retina (Ramachandran et al., 1994). (b,c) Surface manifold output of the model of the perceptual surface reconstruction process by Sarti, Malladi, and Sethian (2000). Model of the perceptual surface reconstruction process. (b) Starting condition of the default surface superimposed on the figure. (c) Development of the surface toward the subjective surface. The original features are mapped in white.