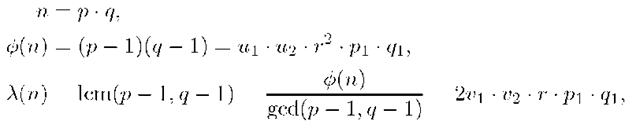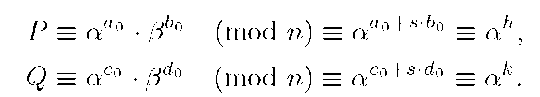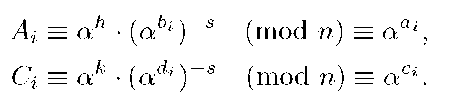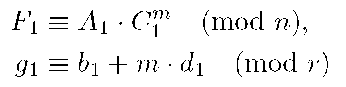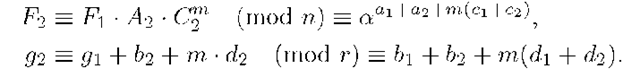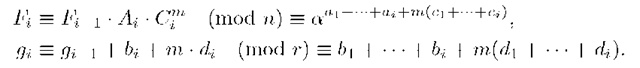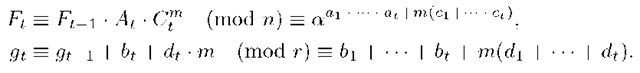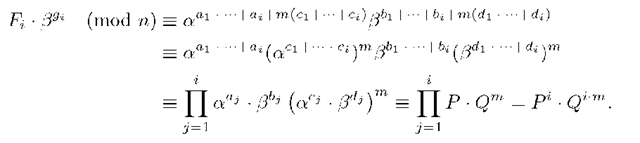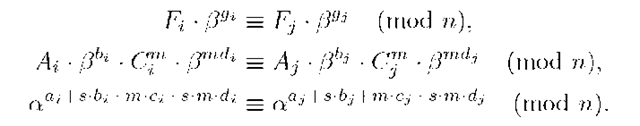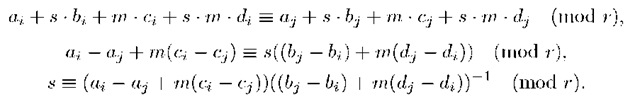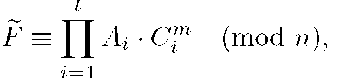Abstract
Multisignature schemes are digital signature schemes that permit one to determine a unique signature for a given message, depending on the signatures of all the members of a specific group. In this work, we present a new semi-short multisignature scheme based on the Subgroup Discrete Logarithm Problem (SDLP) and on the Integer Factorization Problem (IFP). The scheme can be carried out in an on- and off-line basis, is efficient, and the bitlength of the multisignature does not depend on the number of signers.
Keywords: Digital signature, Multisignature, Public key cryptography.
Introduction
There are currently different methods and algorithms to perform, in a safe way, digital signatures. Most of these protocols are based on Public Key Cryptography [1]. The main feature of this kind of cryptography is that each individual has two keys, one public key and one private key. Additionally, to make more efficient the procedures of digital signatures and their electronic transmission, hash functions are used [2]. These functions are publicly known and allow signing a digest of the original document instead of the whole document.
Multisignature schemes are protocols of digital signature whereby a group of users, G = {U\, . .,Ut}, signs a document such that the signature is valid if and only if all members of the group take part in the protocol and the signature verifies a specific condition of validity. These schemes have application in settings such us, for example, corporate scenarios for signing contracts between companies, the government and public administrations, agreements between different organization, etc. The easiest way to carry out a multisignature for a message is to consider as such signature the list formed by all the partial signatures of each one of the signers. However, this signature is not practical since its length is proportional to the number of signers [3,4].
In general, most of the multisignature protocols are performed as follows:
1. The signer Ui signs the original message by using the signer private key.
2. Each one of the following signers, in an ordered way, signs the document, already signed by the one who is previous in the group.
3. The last member of G, Ut, signs the signed document that the previous signer has sent to him and sends to the verifier the original message and the multisignature calculated by the group of signers.
The verifier performs the verification of the multisignature by checking each one of the partial signatures of the group of signers, following the protocol and keeping the order in which they were signed.
The first multisignature scheme was proposed in [5], where a modification of the RSA cryptosystem was performed in such a way that the module considered was the product of three primes instead of just two. In [6] a scheme was proposed where the signature length is similar to the length of a simple signature and shorter than the signature obtained from the scheme proposed in [5]. This proposal can be used only if the cryptosystem is bijective. Other proposals based on the RSA cryptosystems have been proposed [7,8,9,10,11].
Regarding multisignature schemes based on the discrete logarithm problem, in [12] the group of signers must cooperate to sign the message and send the signature to a given group of verifiers. Only the union of all verifiers is able to validate the multisignature. Additionally, the signers must use not only their own private keys, but also the public key of all the verifiers. However, this scheme has some weaknesses [13,14]. The scheme proposed in [15] allows to perform a multisignature if the verifiers of the signature belong to a previously specified group.This scheme has some weaknesses as well [16,17].
In [18] a multisignature scheme for a generic model of public key is presented. The model requires some properties: Each one of the signers must have a certified public key with its corresponding private key, which must be generated by the signer himself. The signers must interact in a given number of rounds. In each round each signer receives a message, performs several calculations and sends another message to the next signer. It must be computationally infeasible to forge a multisignature if there exists one honest signer.
Our multisignature scheme has the property and advantage that each signer has his own private key, but all of them share the same public key. In this sense, the new scheme does not match exactly the model proposed in [18] since the procedure is carried out in just one round in which all the signers participate. Moreover, each signer does not need to have his own certified pair of keys (public and private). In fact, in the protocol all the signers share the same public key, but each one has his own private key. This fact simplifies and spares some of the problems related to the computational effort for computation, bandwidth, and, therefore, the overall efficiency of the proposed protocol.
Our proposal verifies several properties: It is secure, efficient, independent of the number of signers, the signature is determined by all the signers in any previously given order, allows adding new signers, and the verification procedure does require the verification of the partial signature of each member of G.
A Multisignature Scheme Based on SDLP and IFP
We propose a new multisignature scheme whereby each member of a given group, G, signs a document making use of his private key. The verifier of the signature checks whether the signature corresponds to the multisignature of the group, by using the public key that all the members of the group share [19].
We suppose that G = {U1,U2,…,Ut} is the group of signer and T is the Trusted Third Party which computes its own private key, the unique public key associated to all private keys, as well as helps the members of G to generate their private key.
Key Generation
First of all, T generates its own private key:
1. T chooses two large primes p and q such that
with r,pi,qi primes,
with
and
To guarantee the security of the scheme, the bitlength of r is chosen so that the Discrete Logarithm Problem in a Subgroup of Z* , of order r, be computationally infeasible. Although the factors of n are of a particular form, they can be efficiently generated and to our knowledge there is no known efficient algorithm to factorize n ([20], [21]).
2. T computes
where
is the Euler function and
is the Carmichael function. 3. Next, T selects an element
of order r modulo n, verifying
The element a can be efficiently computed due to the fact that T knows the factorization of
[21, Lemma 3.1]. We denote by Sr the multiplicative subgroup of Z*n generated by a. 4. T generates a secret random number
and computes
5. The values (a, r, 3, n) are made public; whereas T keeps secret (p, q, s).
Remark that breaking the key generation protocol amounts to solving the Integer factorization Problem (IFP). Moreover, to determine s from 3 in the expression (1) the Subgroup Discrete Logarithm Problem (SDLP) must be solved.
Before generating the private key of each signer, T generates its private key and the shared public key as follows:
1. T determines its private key by generating four random integer numbers
2. T obtains the common public key by computing
For avoiding T can impersonate any signer of G, an interactive session between each user Ui and T is developed to compute Uj’s private key, i = 1,…,t:
1. Ui generates two secret integers
at random and sends the values of
in a secure way, in order to protect both secret integers. Note that T can determine Ai and Ci since it knows
but it cannot compute ai, ci because it cannot solve the SDLP. In short, each party gets access to only 2 out of the 4 key parameters.
2. T computes
Then T sends to Ui the values of Ai, Ci by using a secure channel. 3. The private key of Ui is the set (bi, d, Ai,, C). Remark that for Ui it is also impossible to compute the values of ai and ci .
Key Verification
To verify the correctness of T’s key, each signer,
tests if
Moreover, each signer must verify that his private key corresponds to the public key (P, Q) by checking the correctness of the following expressions:
In fact, we have:
Signing a Message
We will present a protocol to determine a multisignature of the group G for a given message M , where only the signers participate.
We suppose a secure hash function, (j, has been selected (for example, one of the SHA-2 family) with (j(M) = m. Moreover, it is assumed that the set of signers has been ordered, due to the fact that each signer will sign the signature determined by the previous signer.
The process is as follows: Each signer verifies the partial signature determined by the previous signer, computes his own signature by using the received signature, and sends the new partial signature to the next signer.
1. The first signer, Ui , computes his partial signature for the message M by using his private key, (b1, d1,A1,C1), and m = (j(M):
and sends (F1, g-\) to the second signer, U2. 2. The second signer, U2, verifies U1′s signature checking if
U2 computes his partial signature for the message:
U2 sends (F2,g2) as his partial signature to the third signer.
i. The signer Ui receives the Ui-1 ‘s partial signature
and then verifies this partial signature checking if
Ui computes his partial signature:
Ui sends (Fi,g.i) to the next signer.
t. The last signer in the group, Ut, receives the Ut-1′s partial signature and verifies that signature testing if
Ut computes his partial signature for the message:
Ut makes public the multisignature for M: (F,g) = (Ft,gt).
The verification of each partial signature carried out by each signer (but the first one) is necessary in order to avoid that a signer signs a non-valid message. Moreover, the verification of the Uj’s partial signature is correct because it is
Verifying the Multisignature
Let (F, g) be the multisignature for a message M computed by the group of t signers, G. In order to verify such signature, a verifier must to check if
This verification equation is correct as
Properties and Security Analysis
The proposed multisignature scheme has the following properties:
1. The scheme has a fixed size, i.e., it does not depend on the number of signers.
2. The multisignature is a semi-short signature in the sense that the pair (F, g) is composed by two elements belonging to Z* and to Z*, respectively.
3. The multisignature is efficient as all computations require polynomial time.
4. It is possible to include new signers in the group G without re-execution of the protocol by the rest of the signers. It is possible to place the new signers at the end of the signer group so that each one of them follows the protocol by computing his partial signature from the previously computed multisignature.
5. The multisignature verification process is easy and efficient.
The proposed multisignature scheme is secure since to break the proposed scheme an attacker needs to solve three difficult problems: IFP, DLP, and SDLP. Hence, a signer knowing only his private key cannot determine neither T’s private key nor its secret value s.
In the scheme it is impossible for two signers to compute a forged signature because each signer verifies the signatures of all the previous signers.
Moreover, two or more signers could try to conspire with the goal of obtaining the secret value s of T, and then computing new private keys.
In this attack, if the signers Ui and Uj, j > i, share their signatures (Fi,gi) and (Fj, gj), they know that the following holds
Then, they can suppose that the exponents verify the following equations:
But, none of them can solve this equation because they do not know ai, aj, c-i, cj.
The scheme is secure even if a user has access to the signatures of two distinct messages signed with the same keys because it implies solving IFP and DLP.
Finally, nobody can determine a forged multisignature for the message M without being detected by T. In fact, a forger could know the public key, (P, Q), the message, M, its hash, m, the number of signers, t, and the values
From these data, he can choose an integer g and determine the element
Moreover, he can compute
and publish the pair (F, g) as a multisignature of the signer group G for the message M, that passes the verification equation (2).
Nevertheless, T can prove that this multisignature is a forgery. It is sufficient that it calculates
and shows that
Conclusions
A new semi-short multisignature scheme based on three difficult problems from Number Theory, namely, integer factorization, discrete logarithms, and subgroup discrete logarithms has been proposed. A multisignature (F, g) is semi-short in the sense that
where the bitlength of n is much bigger than the the bitlength of r.
This scheme permits one to obtain a semi-short signature with a fixed bitlength, which is independent of the number of signers.
The multisignature scheme is efficient since the computations only require polynomial time, verifies the conditions of multisignature schemes, and moreover it is secure both against conspiracy attacks and against forgery.
