26.2.
Universal Joints
Universal joints are capable of transmitting torque and rotational motion from one shaft to another when their axes are inclined to each other by some angle, which may constantly vary under working conditions. Universal joints are incorporated in the of vehicle’s transmission system to perform three basic applications :
(a) Propeller shaft end joints between longitudinally front mounted gearbox and rear final drive axle.
(b) Rear axle drive shaft end joints between the sprung final drive and the unsprung rear wheel stub axle.
(c) Front axle drive shaft end joints between the sprung front mounted final drive and the unsprung front wheel steered stub axle.
Universal joints have movement only in the vertical plane when they are used for longitudinally mounted propeller shafts and transverse rear mounted drive shafts. When these joints have been used for front outer drive shaft they have to move in both the vertical and horizontal plane to accommodate both vertical suspension deflection and the swivel pin angular movement to steer the front road wheels. The compounding of angular working movement of the outer drive shaft steering joint in two planes imposes large and varying working angles even when the torque is being transmitted to the stub axle. Due to the severe working conditions, special universal joints known as constant velocity joints are employed. These joints have been designed to absorb torque and speed fluctuations and to operate reliably with very little noise and wear having long life.
26.2.1.
Basic Types of Universal Joints Cross-type Joint.
This type of joint is also called a Hooke-type coupling as it was developed from the joint invented by Robert Hooke in the seventeenth century. This joint is commonly used today. The joints in Fig. 26.8A and B represent the basic and developed forms respectively. They use two yokes set at 90 degrees to each other and a cross-shaped trunnion block joins these yokes. In more developed joints like Hardy Spicer type, contact between the two parts is made by needle roller bearings held in a hardened steel cup retained in each arm of the yoke. For the alignment of the trunnion, the bottom of the cup forms a contact with the end of the block.
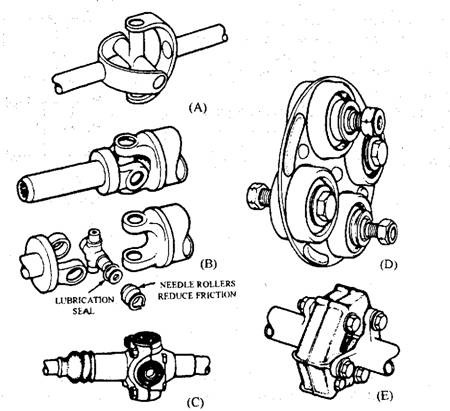
Fig. 26.8. Types of universal joints. A. Hooke-type joint. B. Cross type joint (Hardy Spicer).
C. Cross-type with rubber bushing. D. Layrub.
E. Doughnut rubber coupling.
A special viscous oil, similar to that used in a final drive, is used for bearing lubrication, which is contained in a reservoir formed by drilling out the centre of the trunnion arms. The oil is introduced by a lubrication hippie or is prefilled once for entire life. An oil seal, retained on each arm of the block, prevenjts the escape of the lubricant. The cups are held in the yoke either by circlips or staking. The replacement of worm parts in the joint becomes more difficult due to peening over the edge of the yokes to stake the cups. Therefore replacement of the complete shaft assembly is recommended when the joint is worn. These joints offer several advantages such as they (i) are compact, (££) have high mechanical efficiency, (Hi) have ability to drive through a large occasional ‘bump’ angle (maximum about 25 degrees), and (iv) due to accurate centring of shaft, are suitable for high speed operation. One major disadvantage of the cross-type joint is its inadequate flexibility to absorb torsional shocks and drive-line vibrations, especially when a comparatively rigid transmission system is used.
Lubrication failure, especially when a grease nipple in the trunnion block is missed, causes the needle rollers to indent the bearing surfaces. This type of wear causes a slight angular movement and produces a noise, commonly described as a clonk, during the change over from drive to over-run and vice versa. If this fault is not rectified in time, the rate of wear accelerates leading to misalignment and severe vibration.
Rubber Joints.
A smoother and less harsh drive is obtained by incorporating one or more rubber joints in the transmission driveline. Three types of rubber joints in use include moulton, layrub and doughnut.
Moulton Joint.
This rubber trunnion type joint (Fig. 26.8C) is based on a hooke type coupling. It uses moulded rubber bushings for the transmission of drive between the trunnion and yokes. These synthetic rubber mouldings require no lubrication and due to high flexibility they damp the torsional shocks produced when the drive is transmitted through an angle.
Layrub Joint.
This type joint (Fig. 26.8D), originally made by the Laycock company, was constructed of a series of rubber bushings. The name layrub is used to describe this joint. It uses a number of moulded rubber blocks, with specially shaped cavities at the ends. These blocks are sandwiched between two steel pressings. Each shaft is connected by means of a fork to alternate rubber blocks. This arrangement permits the rubber blocks to deform making the drive possible for transmission through a small angle. Also the blocks accommodate small axial and angular movements for shaft length alteration and torsional damping. This coupling is relatively large in diameter. The layrub type joint offers several advantages, such as (i) it does not require lubrication,
(ii) it is capable of driving through bump angles up to about 15 degrees, (Hi) it allows for axial movement, requiring no splining of the shaft,and (iv) its resilience damps shocks and insulates vehicle from transmission noise.
Doughnut Joint.
Although large in size, the great flexibility of this joint provides soft cushioning. This absorbs the majority of torsional shocks generated by the action of other joints or by vibration from either the engine or road wheel. The synthetic rubber coupling shown in Fig. 26.8E is near-circular in shape and is moulded around cylindrical steel inserts, which are bolted alternatively to the three-arm forks fixed to the shafts. The merits of this coupling are similar to that of layrub joint.
26.2.2.
Speed Variation of a Hooke-type Joint due to Drive and Driven Shaft Inclination
When a hooke-type coupling transmits a drive through an angle, the output shaft does not rotate through 360 degrees at a constant speed. Instead the speed varies every 90 degrees of rotation, and the rate of movement for one revolution is fast, slow, fast, slow (Fig. 26.9). This cyclic speed variation, and its associated vibration, is insignificant when the drive angle is less than about 5 degrees, but becomes much more intense as the angle is increased.
A simplified sketch of a Hooke’s joint is shown if Fig. 26.10, in which the driving shaft A is connected to the arm YY of the central cross-piece through the driving yoke, and the remaining arm, XX of the cross-piece connects to the driven shaft B through driven yoke. The driving yoke lies in the vertical plane with its axis YY vertical, and the driven yoke lies in a plane inclined at an angle 0 to the horizontal with its axis XX horizontal.
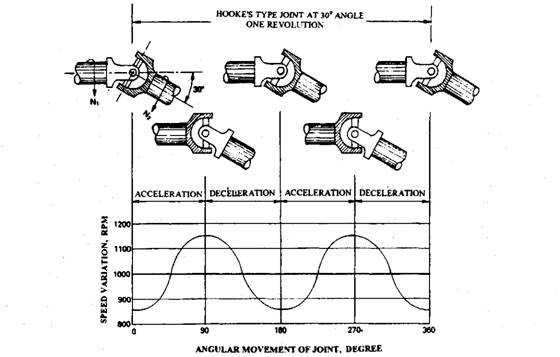
Fig. 26.9. Speed variation with Hooke-type joints.
Let the driving shaft is turned through an angle a so that the point Y moves to Yi as shown in end view in Fig. 26.10. The point X moves about axis OB, through an angle 4> subtended by an arc Xd and it moves in a vertical plane to point Xi through an elliptical path.
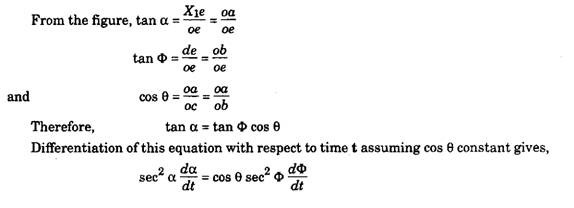

Fig. 26.10. Simplified diagram of a Hooke’s joint.
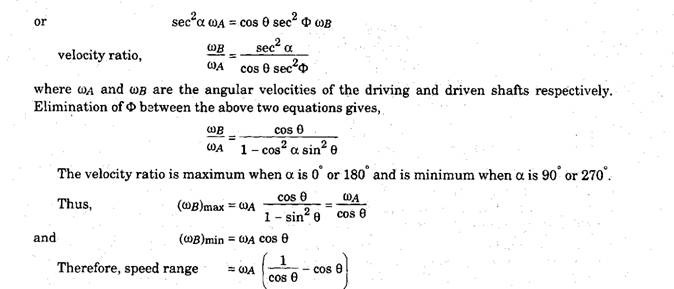
Due to the above variation of the speed of the driven shaft for various positions of the driving shaft, a single Hooke’s joint becomes unsuitable for the power transmission in automobiles. But a constant velocity ratio can be obtained by the correct use of a double joint.
The acceleration of the driven shaft, as may be obtained by differentiating the equation for velocity ratio with respect to time.
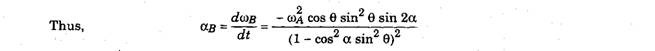
To achieve a constant speed output from the propeller shaft two Hooke-type couplings can be mounted either back-to-back or positioned in a certain way at each end of the propeller shaft. In both the configurations the relative positions of each coupling must be such that the speed
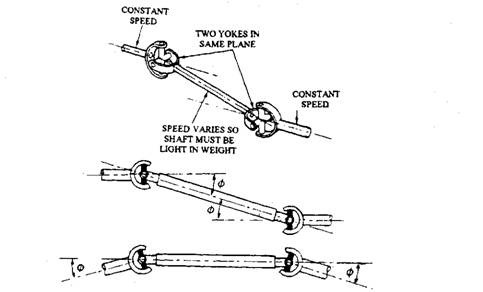
Fig. 26.11. Phasing of Hooke-type couplings.
change of one coupling is counteracted by the other. The phasing of Hooke-type couplings, as applied to two separate driveline layouts, is illustrated in Fig. 26.11.
From this diagram it can be seen that to obtain a constant speed,
(i) yokes at each end of the propeller shaft must be placed in the same plane, and
(ii) drive angle of each coupling must be equal.
A constant velocity (CV) joint imply that when two shafts are inclined to one another at some angle and are coupled together by some sort of joint, then a uniform input speed transmitted to the output shaft produces the same angular output speed throughout one revolution. There are no angular acceleration and deceleration as the shafts rotate. Various CV joints in use have a construction, which is based on either the twin hooke-type coupling arrangement or the angle bisects principle. The CV joints in use include :
• Tracta • Rzeppa
• Weiss • Tripode
o
Example 26.3. Two shafts, the axles of which intersect but are inclined at 20 to each other, are connected by a Hooke’s joint. If the driving shaft has a uniform speed of1000 rpm., find from first principles, the variation in speed of the driven shaft. The driven shaft carries a rotating mass, which weighs 147 N and has a radius of gyration of 0.25 m. Find the accelerating torque
on the driven shaft for the position when the driven shaft has turned 45 from the position in which its fork end is in the plane containing the two shafts.

26.2.3.
Double Hooke’s Type CV Joint
One method of obtaining very near constant velocity characteristics is to position two Hooke’s joints back to back so that their yoke arms remain in line with one another (Fig. 26.12).
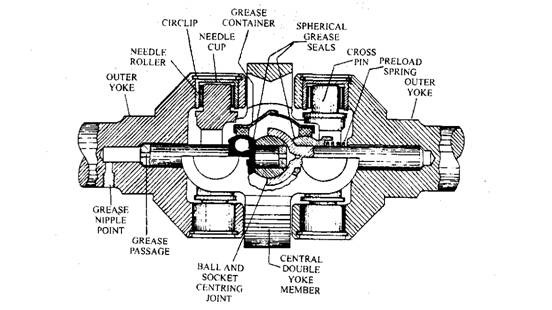
Fig. 26.12. Double Hooke’s type constant velocity joint.
After assembly, both pairs of outer yoke arms must be at right angles to the arms of the central double yoke member. This double joint combination can be considered in two stages. The first stage hinges the drive yoke and driven central double yoke together, and the second stage links the central double yoke (now drive member) to the driven final output yoke. Consequently, the second stage drive half of the central double yoke is placed a quarter of a revolution out of phase with the first stage drive yoke (Fig. 26.13).
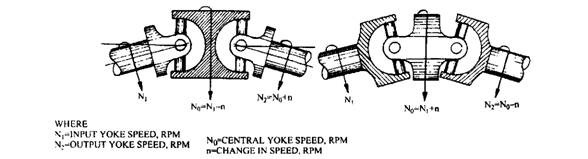
Fig. 26.13. Double Hooke’s type joint shown in two positions 90 degrees out of phase.
Therefore, if the input and output shafts are inclined to each other and the first stage driven central double yoke is speeding up, then the second stage driven output yoke slows down. On the other hand when the first stage driven member reduces its speed the second stage driven member increases its speed. The speed lost or gained by one half of the joint equals that gained or lost by the second half of the joint respectively. As a result no cyclic speed fluctuation occurs between input and output shafts during rotation.
This double joint incorporates a centring device (Fig. 26.12) normally of the ball and socket spring loaded type. This device maintains equal angularity of both the input and output shafts relative to the central double yoke member. Although this is a difficult task to execute due to the high end loads experienced by the sliding splined joint of the drive shaft, but the accuracy of centralizing the double yokes is not critical at the normal relatively low drive shaft speeds.
This double Hooke’s joint is specifically suitable for heavy duty vehicles with rigid front wheel drive live axle requiring large lock to lock wheel swivel. This type of joint is relatively large in size compared to its torque transmitting capacity. This forms a major limitation with this joint.
Velocity Ratio.
Double hooke’s joint (Fig. 26.14) connects driving shaft A and driven shaft B which are parallel but lie in different axis through an intermediate shaft C. The yokes of shaft A and B lie in the same plane and the two yokes of shaft C also lie in another plane. The correct positioning of the yokes specially those on the intermediate shaft is essential to keep the angles same for both joints and thus to obtain constant velocity ratio.
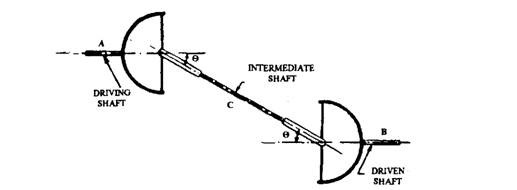
Fig. 26.14. Simplified diagram of a double Hooke’s joint.
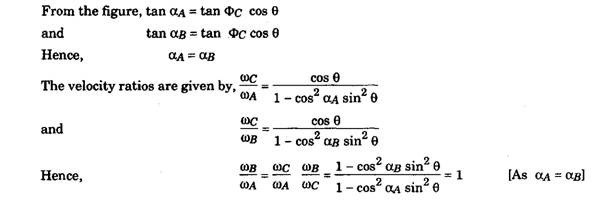
26.2.4.
Tracta Constant Velocity Joint
The tracta constant velocity joints was invented by Fennille in France and was later manufactured by Bendix Limited in England. In some respect these joints are similar in action to a double Hooke’s type constant velocity joint. This type of joint incorporates two outer yoke
jaws members and two intermediate semispherical members (Fig. 26.15A). Each yoke jaw engages a circular groove formed on the intermediate members. Both intermediate members are coupled together in turn by a swivel tongue and grooved joint.
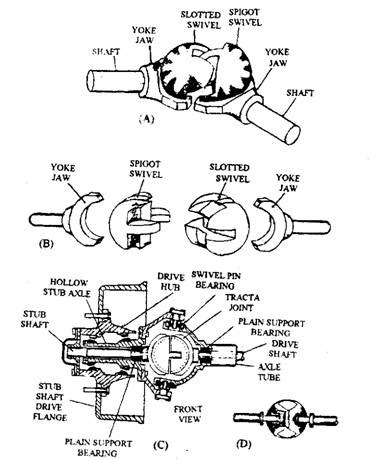
Fig. 26.15. Bendix tracta joint. A. Pictorial view. B. Exploded view.
C. Front wheel drive hub swivel pins and axle incorporating a tracta joint.
D. Plan view.
Relative motion between the outer jaw yokes and the intermediate spherical members is provided by the yoke jaw, which is fitted into circular grooves formed in each intermediate member. Relative movement between adjacent intermediate members takes place due to a double tongue formed on one member slotting into a second circular groove, which is cut at right angles to the jaw grooves (Fig. 26.15B). In normal position, both the outer yoke jaws are in alignment, but the central tongue and groove part of the joint remains at right angles to them. When the input and output shafts are inclined at some working angle to each other, the driving intermediate member accelerates and decelerates during each revolution. Since the central tongue and groove joint are a quarter of a revolution out of phase with the yoke jaws, the corresponding speed fluctuation of the driven intermediate and output jaw members exactly counteract and neutralize the speed variation of input half member. Thus the output speed change is identical to that of the input drive, providing constant velocity rotation.
Since roiling motion takes place between members of this type of joint, friction losses are slightly higher than for couplings. But, due to the large flat rubbing surfaces in contect the joint has large torque transmitting capability. Although the size of these joints are fairly large compared to other types of constant velocity joint arrangements, but these joints provide constant velocity rotation at angles up to 50 degrees. A tracta joint incorporated in a rigid front wheel drive axle is shown in (Fig. 26.15C and D).
26.2.5.
Rzeppa Joint
A Ford engineer, Alfred Hans Rzeppa (pronounced sheppa) invented one of the first practical constant velocity joints in 1926. This joint was able to transmit torque over a wide range of angles. An improved version of the joint was patented by Rzeppa in 1935. This version uses six balls as intermediate members, which are kept at all times in a plane bisecting the angle between the input and output shafts (Fig. 26.16). A controlled guide ball cage is incorporated, which maintains the balls in the bisecting plane (or the median plane) by means of a pivoting control strut, which swivels the cage at the correct angle. This control strut is located in the centre of the enclosed end of the outer cup member. Both ball ends of the strut are positioned in a recess and socket formed in the adjacent ends of the driving and driven members of the joint respectively. A large spherical waist approximately midway along the strut aligns with a hole made in the centre of the cage. Any angular inclination of the two shafts at any instant deflects the strut, which in turn proportionally swivels the control ball cage at half the relative angular movement of both shafts. This method of cage control has a tendency to jam and, therefore, suffers from mechanical wear.
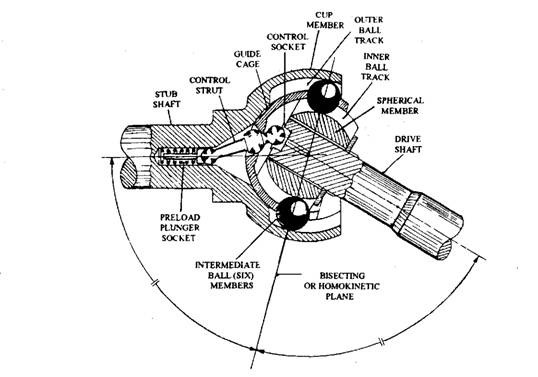
Fig. 26.16. Early Rzeppa constant velocity joint.
Birfield Joint.
The Birfield joint, manufactured by Hardy Spicer Limited, is based on the Rzeppa principle (Fig. 26.17). In this construction the joint’s performance has been improved further by incorporating converging ball tracks, which do not rely on a controlled ball cage to maintain the intermediate ball members on the median plane (Fig. 26.17B). This Joint uses an inner (ball) input member driving an outer (cup) member. Torque is transmitted from the input to the output member again by six intermediate ball members, which fit into curved rack grooves formed in both the cup and spherical members. Articulation of the joint takes place due to rolling of the balls in between the inner and outer pairs of curved grooves.
Constant velocity conditions are achieved by an intermediate member, formed by a ring of six balls placed in the median plane (Fig. 26.17B) of the shape of the curved ball tracks generated in both the input and output joint members.
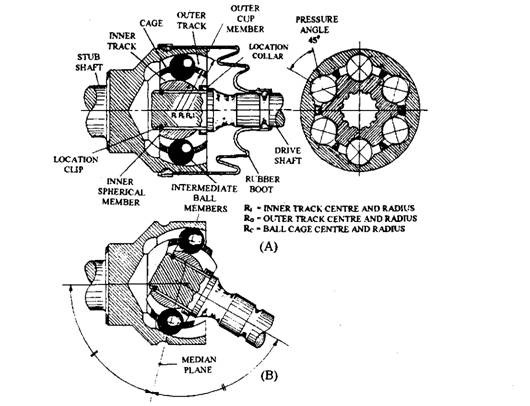
Fig. 26.17. Birfield. Rzeppa type constant velocity joint. A. Side and end view. B. With 30 degrees shaft angularity.
In order to obtain a controlled movement of the intermediate balls, the tracks (grooves) are formed on semicircles in both halves, inner and outer members. The centres are on either side of the joint’s geometric centre by an equal distance (Figs. 26.17A and 26.18). Once the inner member aligns inside the outer one, the six matching pairs of tracks from grooved tunnels in which the balls are sandwiched. The inner and outer track arc offset centre from the geometric joint centre is so chosen to give an angle of convergence (Fig. 26.18) marginally larger than 11
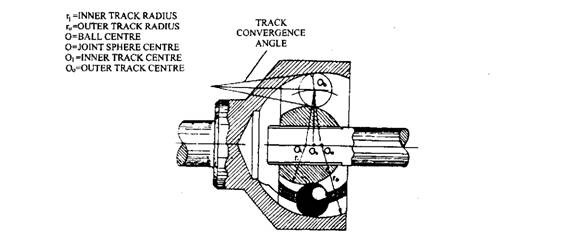
Fig. 26.18. Birfield Rzeppa type joint showing ball track convergence.
degrees.
This is the minimum angle required to positively guide and hold the balls on the median plane over the entire angular inclination movement of the joint.
The ball tracks in the inner and outer members are slightly elliptical in section, having effectively two centres of curvature (Fig. 26.19) instead of a single semicircle arc. The radius of curvature of the tracks on each side of the ball at the four pressure angle contact points is larger than the ball radius. The pressure angle is equal in the inner and outer tracks due to which the balls are all under pure compression at all times so that the limiting stress is raised and consequently the loading capacity of the balls is also raised.
The ratio of track curvature radius to the ball radius is known as the conformity ratio, which is selected to achieve a 45 degrees pressure angle point contact. This provides effective and durable service in transmitting the torque from the driving to the driven half members of the joint (Fig. 26.19). When the balls move under load to and fro in their respective tracks, a certain amount of roll and slide takes place. With a pressure angle of 45 degrees, the roll to sliding ratio is roughly 4:1 which is sufficient to minimize the contact friction during any angular movement of the joint.
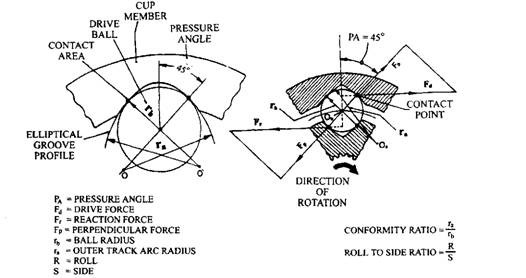
Fig. 26.19. Birfield joint track groove profile.
Both the inner drive and outer driven members of the joint have spherical external and internal surfaces respectively. Also, the six ball intermediate members of this joint are positioned in their respective tracks by a cage which has the same centre of arc curvature as the input and output members (Fig. 26.17C). The space between the spherical surfaces of both male inner and female outer members is taken up by the cage, which also provides the central pivot alignment for the two halves of the joint when the input and output shafts are inclined to each other (Fig. 26.17B). Additionally the overall alignment of all the balls on the median plane is provided by the cage.
The efficiency of these joints is high, ranging from 95% to 100% with the joint working angle 45 degrees and zero respectively. Losses are mainly due to the internal friction between the balls and their respective tracks, which depends on ball load, speed and working angle, and by the viscous drag of the lubricant.
The diagnosis of front wheel drive constant velocity joint wear or damage can be narrowed down by turning the steering to full lock and driving the vehicle round in a circle. If the steering or transmission now indicates signs of excessive vibration or clunking and ticking noises are heard coming from the drive wheels, then further investigation of the front wheel joints is necessary. Split rubber gaiters used to protect the constant velocity joints can considerably shorten the life of a joint because of exposure to the weather and abrasive grit entering into the joint mechanism.
26.2.6.
Carl Weiss Constant Velocity Joint
A successful constant velocity joint was invented and patented by Carl W. Weiss of New York, USA, in 1925. Subsequently, the Bendix Products Corporation developed the Weiss constant velocity principle further and manufactured this design of joint (Fig. 26.20).
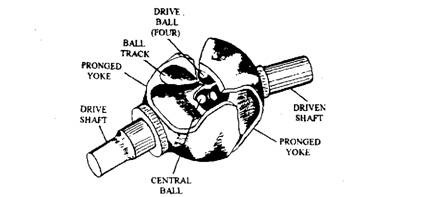
Fig. 26.20. Pictorial view of Bendix Weiss constant velocity type joint (pictorial view).
This type of time constant velocity joint incorporates double prong (arm) yokes, mounted on the ends of the two driving shafts. Four (either curved or straight) ball track grooves (Fig. 26.21) are ground inside each prong member. Each yoke arm of one member is assembled in between the prong of the other member and four balls located in adjacent grooved tracks transmit the drive from one yoke member to the other. The intersection of each matching pair of grooves maintains the balls in a bisecting plane created between the two shafts, even when one shaft is inclined to the other (Fig. 26.22). Some joint models depending upon application use a fifth centralizing ball in between the two yokes. The versions, usually with straight ball tracks, do not have the central ball due to which it can accommodate a degree of axial plunge, especially if, the balls roll rather than slide as claimed.
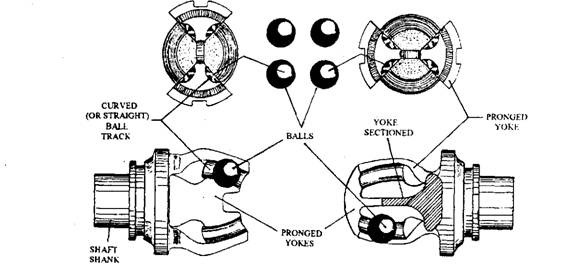
Fig. 26.21. Carl Wiess type joint (side and end view).
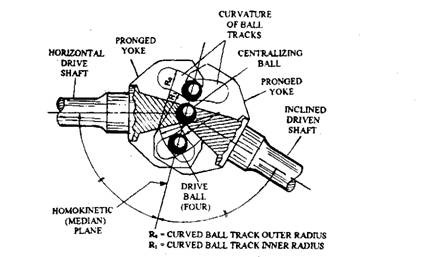
Fig. 26.22. Principle of Bendix Wiess constant velocity type joint.
Carl Weiss Constant Velocity Principle.
The geometric construction of the upper half of the joint (Fig. 26.23) is considered. The ball track curvatures on the left and right hand yokes are represented by circular arcs with radius r and centres of curvature L and R on their respective shaft axes when both shafts are in line. The centre of the joint is at point O and the intersection of both the ball track arc centres occur at point P. Triangle LOP equals triangle ROP with sides LP and RP being equal to the radius of curvature. The offset of the, centres of track curvature from the joint centre are LO and RO, therefore sides LP and RP are also equal. Now, angles LOP and ROP are two right angles and their sum equals to the angle LOR, i.e. 180 degrees. Hence point P lies on a perpendicular plane, which intersects the centre of the joint. This plane is known as the median (homo-kinetic) plane.
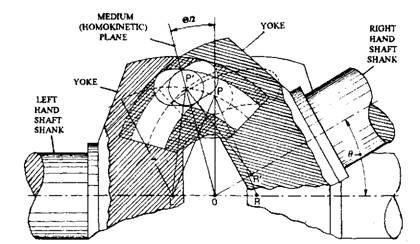
Fig. 26.23. Geometry of Carl Weiss type joint.
If the right hand shaft is now swivelled to produce a working angle 8, its new centre of track curvature becomes R’ and the intersection point of both yoke ball track curvatures is now P’ (Fig. 26.23). Therefore triangle LOP’ and ROP’ are equal since both share the same bisecting plane of the left and right hand shafts. Thus sides LP’ and RP’ are also equal to the track radius of curvature r and that the offset of the centres of OR’ and OR are equal to LO. Consequently, angle LOP equals angle R’OP’ and the sum of the angles LOP’ and R’OP’ equals angle LOR’ which is (180 – 9). Therefore angle LOP equals angle ROP, which is (180 – 9)/2. Since P’ bisects the angle made between the left and right hand shaft axes it must lay on the median (homo-kinetic) plane.
The angle produced by the ball track curvature intersecting point line projected to the centre of the joint is always half the working angle 0 made between the two shaft axes and fixes the position of the driving balls. The geometry of the intersecting circular arcs therefore forces the balls to be in the median (homo-kinetic) plane at any instant.
26.2.7.
Tripode (Tripot) Type CV Joint
This joint is compact and as it can operate efficiently at high speed, it is more common in vehicles. The joint provides good resistance to high-speed centrifugal effects. The design of this joint, and manufacturing with the reduced working clearances provide a transmission drive line with good noise-vibration harshness (NVH) performance. The construction illustrated in Fig. 26.24 incorporates three armed support (tripode) carrying the spherically shaped rollers, fixed to the outer housing. On both sides of each driving fork, which also has three arms, grooves are cut to form a bearing track for the rollers.
The force exerted by the side of the driving fork on the rollers produces the drive through the joint. This force is transmitted to the tripode and joint housing. Changes in the drive angle causes the roller to move backwards and forwards along the grooved track as the joint rotates through one revolution. A small clearance is given between the roller and track to permit this movement. The tripode joint provides constant velocity motion because of the path taken by the rollers with respect to the contact point on the track. This type of fixed joint can work occasionally up to a drive angle of about 45 degrees.
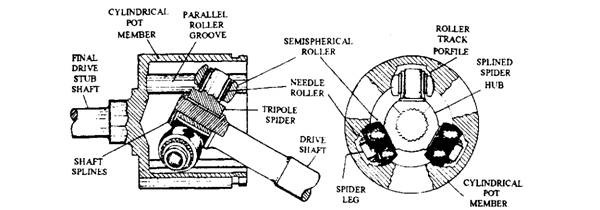
(A) Fig. 26.24. Tripot CV joint. (B)
