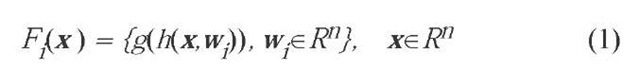INTRODUCTION
Supervised Artificial Neural Networks (ANN) are information processing systems that adapt their functionality as a result of exposure to input-output examples. To this end, there exist generic procedures and techniques, known as learning rules. The most widely used in the neural network context rely in derivative information, and are typically associated with the Multilayer Perceptron (MLP). Other kinds of supervised ANN have developed their own techniques. Such is the case of Radial Basis Function (RBF) networks (Poggio & Girosi, 1989). There has been also considerable work on the development of adhoc learning methods based on evolutionary algorithms.
BACKGROUND
The problem of learning an input/output relation from a set of examples can be regarded as the task of approximating an unknown function from a set of data points, which are possibly sparse. Concerning approximation by classical feed-forward ANN, these networks implement a parametric approximating function and have been shown to be able of representing generic classes of functions (as the continuous or integrable functions) to an arbitrary degree of accuracy. In general, there are three questions that arise when defining one such parameterized family of functions:
1. What is the most adequate parametric form for a given problem?
2. How to find the best parameters for the chosen form?
3. What classes of functions can be represented and how well?
The most typical problems in a ANN supervised learning process, besides the determination of the learning parameters themselves, include (Hertz, Krogh & Palmer, 1991), (Hinton, 1989), (Bishop, 1995):
1. The possibility of getting stuck in local optima of the cost function, in which conventional non-linear optimization techniques will stay forever. The incorporation of a global scheme (like multiple restarts or an annealing schedule) is surely to increase the chance of finding a better solution, although the cost can become prohibitedly high. A feed-forward network has multiple equivalent solutions, created by weight permutations and sign flips. Every local minima in a network with a single hidden layer of h?1 units has s^) =/?1 !2h1 equivalent solutions, so the chances of getting in the basin of attraction of one of them are reasonable high. The complexity of the error surface -especially in very high dimensions- makes the possibility of getting trapped a real one.
2. Long training times, oscillations and network paralysis. These are features highly related to the specific learning algorithm, and relate to bad or too general choices for the parameters of the optimization technique (such as the learning rate). The presence of saddle points—regions where the error surface is very flat—also provoke an extremely slow advance for extensive periods of time. The use of more advanced methods that dynamically set these and other parameters can alleviate the problem.
3. Non-cumulative learning. It is hard to take an already trained network and re-train it with additional data without losing previously learned knowledge.
4. The curse of dimensionality, roughly stated as the fact that the number of examples needed to represent a given function grows exponentially with the number of dimensions.
5. Difficulty of finding a structure in the training data, possibly caused by a very high dimension or a distorting pre-processing scheme.
6. Bad generalization, which can be due to several causes: the use of poor training data or attempts to extrapolate beyond them, an excessive number of hidden units, too long training processes or a badly chosen regularization. All ofthem can lead to an overfitting of the training data, in which the ANN adjusts the training set merely as an interpolation task.
7. Not amenable to inspection. It is generally arduous to interpret the knowledge learned, especially in large networks or with a high number of model inputs.
LEARNING IN RBF NETWORKS
A Radial Basis Function network is a type of ANN that can be viewed as the solution of a high-dimensional curve-fitting problem. Learning is equivalent to finding a surface providing the best fit to the data. The RBF network is a two-layered feed forward network using a linear transfer function for the output units and a radially symmetric transfer function for the hidden units. The computation of a hidden unit is expressed as the composition of two functions, as:
with the choice h(x,w1)= Hx-wJI/Q (or other distance measure), with 9>0 a smoothing term, plus an activation g which very often is a monotonically decreasing response from the origin. These units are localized, in the sense that they give a significant response only in a neighbourhood of their centre wi. For the activation function a Gaussian g(z)=exp(-Z2/2) is a preferred choice.
Learning in RBF networks is characterized by the separation of the process in two consecutive stages (Haykin, 1994), (Bishop, 1995):
1. Optimize the free parameters of the hidden layer (including the smoothing term) using only the (x)i in D. This is an unsupervised method that depends on the input sample distribution.
2. With these parameters found and frozen, optimize the (c}, the hidden-to-output weights, using the full information in D. This is a supervisedmethod that depends on the given task.
There are many ways of optimizing the hidden-layer parameters. When the number of hidden neurons equals the number of patterns, each pattern may be taken to be a center of a particular neuron. However, the aim is to form a representation of the probability density function of the data, by placing the centres in only those regions of the input space where significant data are present. One commonly used method is the k-means algorithm (McQueen, 1967), which in turn is an approximate version of the maximum-likelihood (ML) solution for determining the location ofthe means of a mixture density of component densities (that is, maximizing the likelihood of the parameters with respect to the data). The Expectation-Maximization (EM) algorithm (Duda & Hart, 1973) can be used to find the exact ML solution for the means and covariances of the density. It seems that EM is superior to k-means (Nowlan, 1990). The set of centres can also be selected randomly from the set of data points.
The value of the smoothing term can be obtained from the clustering method itself, or else estimated a posteriori. One popular heuristic is:
where d is the maximum distance between the chosen centers and M is the number of centers (hidden units). Alternatively, the method of Distance Averaging (Moody and Darken, 1989) can be used, which is the global average over all Euclidean distances between the center of each unit and that of its nearest neighbor.
Once these parameters are chosen and kept constant, assuming the output units are linear, the (square) error function is quadratic, and thus the hidden-to-output weights can be fast and reliably found iteratively by simple gradient descent over the quadratic surface of the error function or directly by solving the minimum norm solution to the over determined least-squares data fitting problem (Orr, 1995).
The whole set of parameters of a RBF network can also be optimized with a global gradient descent procedure on all the free parameters at once (Bishop, 1995), (Haykin, 1994). This brings back the problems of local minima, slow training, etc, already discussed. However, better solutions can in principle be found, because the unsupervised solution focuses on estimating the input probability density function, but the resulting disposition may not be the one minimizing the square error.
EVOLUTIONARY LEARNING ALGORITHMS
The alternative to derivative-based learning algorithms (DBLA) are Evolutionary Algorithms (EA) (Back, 1996). Although the number of successful specific applications of EA is counted by hundreds (see (Back, Fogel & Michalewicz, 1997) for a review), only Genetic Algorithms or GA (Goldberg, 1989) and, to a lesser extent, Evolutionary Programming (Fogel, 1992), have been broadly used for ANN optimization, since the earlier works using genetic algorithms (Montana & Davis, 1989). Evolutionary algorithms operate on a population of individuals applying the principle of survival of the fittest to produce better approximations to a solution. At each generation, a new population is created by selecting individuals according to their level of fitness in the problem domain and recombining them using operators borrowed from natural genetics. The offspring also undergo mutation. This process leads to the evolution of populations of individuals that are better suited to their environment than the individuals that they were created from, just as in natural adaptation.
There are comprehensive review papers and guides to the extensive literature on this subject: see (Shaffer, Whitley & Eshelman, 1992), (Yao, 1993), (Kus?u & Thornton, 1994) and (Balakrishnan & Honavar, 1995). One of their main advantages over methods based on derivatives is the global search mechanism. A global method does not imply that the solution is not a local optimum; rather, it eliminates the possibility of getting caught in local optima. Another appealing issue is the possibility of performing the traditionally separated steps of determining the best architecture and its weights at the same time, in a search over the joint space of structures and weights. Another advantage is the use of potentially any cost measure to assess the goodness of fit or include structural information. Still another possibility is to embody a DBLA into a GA, using the latter to search among the space of structures and the DBLA to optimize the weights; this hybridization leads to extremely high computational costs. Finally, there is the use of EA solely for the numerical optimization problem. In the neural context, this is arguably the task for which continuous EA are most naturally suited. However, it is difficult to find applications in which GA (or other EA, for that matter) have clearly outperformed DBLA for supervised training of feed-forward neural networks (Whitley, 1995). It has been pointed out that this task is inherently hard for algorithms that rely heavily on the recombination of potential solutions (Radcliffe, 1991). In addition, the training times can become too costly, even worse than that for DBLA.
In general, Evolutionary Algorithms -particularly, the continuous ones- are in need of specific research devoted to ascertain their general validity as alternatives to DBLA in neural network optimization. Theoretical as well as practical work, oriented to tailor specific EA parameters for this task, together with a specialized operator design should pave the way to a fruitful assessment of validity.
FUTURE TRENDS
Research in ANN currently concerns the development of learning algorithms for weight adaptation or, more often, the enhancement of existing ones. New architectures (ways of arranging the units in the network) are also introduced from time to time. Classical neuron models, although useful and effective, are lessened to a few generic function classes, of which only a handful of instances are used in practice.
One of the most attractive enhancements is the extension of neuron models to modern data mining situations, such as data heterogeneity. Although a feedforward neural network can in principle approximate an arbitrary function to any desired degree of accuracy, in practice a pre-processing scheme is often applied to the data samples to ease the task. In many important domains from the real world, objects are described by a mixture of continuous and discrete variables, usually containing missing information and characterized by an underlying vagueness, uncertainty or imprecision. For example, in the well-known UCI repository (Murphy & Aha, 1991) over half of the problems contain explicitly declared nominal attributes, let alone other discrete types or fuzzy information, usually unreported. This heterogeneous information should not be treated in general as real-valued quantities. Conventional ways of encoding non-standard information in ANN include (Prechelt, 1994), (Bishop, 1995), (Fiesler & Beale, 1997):
Ordinal variables. These variables correspond to discrete (finite) sets of values wherein an ordering has been defined (possibly only partial). They are more than often treated as real-valued, and mapped equidistantly on an arbitrary real interval. A second possibility is to encode them using a thermometer. To this end, let k be the number of ordered values; k new binary inputs are then created. To represent value i, for 1<i<k, the leftmost 1,…,i units will be on, and the remaining i+1,…,k off.
The interest in these variables relies in that they appear frequently in real domains, either as symbolic information or from processes that are discrete in nature. Note that an ordinal variable need not be numerical.
Nominal variables Nominal variables are unanimously encoded using a 1-out-of-k representation, being k the number of values, which are then encoded as the rows of the identity matrix.
Missing values Missing information is an old issue in statistical analysis (Little & Rubin, 1987). There are several causes for the absence of a value. They are very common in Medicine and Engineering, where many variables come from on-line sensors or device measurements. Missing information is difficult to handle, especially when the lost parts are of significant size. It can be either removed (the entire case) or “filled in” with the mean, median, nearest neighbour, or encoded by adding another input equal to one only if the value is absent and zero otherwise. Statistical approaches need to make assumptions about or model the input distribution itself. The main problem with missing data is that we never know if all the efforts devoted to their estimation will revert, in practice, in better-behaved data. This is also the reason why we develop on the treatment of missing values as part of the general discussion on data characteristics. The reviewed methods pre-process the data to make it acceptable by models that otherwise would not accept it. In the case of missing values, the data is completed because the available neural methods only admit complete data sets.
Uncertainty. Vagueness, imprecision and other sources of uncertainty are considerations usually put aside in the ANN paradigm. Nonetheless, many variables in learning processes are likely to bear some form of uncertainty. In Engineering, for example, on-line sensors are likely to get old with time and continuous use, and this may be reflected in the quality of their measurements. In many occasions, the data at hand are imprecise for a manifold of reasons: technical limitations, a veritable qualitative origin, or even we can be interested in introducing imprecision with the purpose of augmenting the capacity for abstraction or generalization (Esteva, Godo & Garcia), possibly because the underlying process is believed to be less precise than the available measures.
In Fuzzy Systems theory there are explicit formalisms for representing and manipulating uncertainty, that is precisely what the system best models and manages. It is perplexing that, when supplying this kind of input/output data, we require the network to approximate the desired output in a very precise way. Sometimes the known value takes an interval form: “between 5.1 and 5.5″, so that any transformation to a real value will result in a loss of information. A more common situation is the absence of numerical knowledge. For example, consider the value “fairly tall” for the variable height. Again, Fuzzy Systems are comfortable, but for an ANN this is real trouble. The integration of symbolic and continuous information is also important because numeric methods bring higher concretion, whereas symbolic methods bring higher abstraction. Their combined use is likely to increase the flexibility of hybrid systems. For numeric data, an added flexibility is obtained by considering imprecision in their values, leading to fuzzy numbers (Zimmermann, 1992).
CONCLUSION
As explained at length in other chapters, derivative-based learning algorithms make a number of assumptions about the local error surface and its differentiability. In addition, the existence of local minima is often neglected or overlooked entirely. In fact, the possibility of getting caught in these minima is more than often circumvented by multiple runs of the algorithm (that is, multiple restarts from different initial points in weight space). This “sampling” procedure is actually an implementation of a very naive stochastic process. A global training algorithm for neural networks is the evolutionary algorithm, a stochastic search training algorithm based on the mechanics of natural genetics and biological evolution. It requires information from the objective function, but not from the gradient vector or the Hessian matrix and thus it is a zero-order method. On the other hand, there is an emerging need to devise neuron models that properly handle different data types, as is done in support vector machines (Shawe-Taylor & Cristianini, 2004), where kernel design is a current research topic.
key terms
Architecture: The number of artificial neurons, its arrangement and connectivity.
Artificial Neural Network: Information processing structure without global or shared memory that takes the form of a directed graph where each of the computing elements (“neurons”) is a simple processor with internal and adjustable parameters, that operates only when all its incoming information is available.
EvolutionaryAlgorithm: A computer simulation in which a population of individuals (abstract representations of candidate solutions to an optimization problem) are stochastically selected, recombined, mutated, and then removed or kept, based on their relative fitness to the problem.
Feed-Forward Artificial Neural Network: Artificial Neural Network whose graph has no cycles.
Learning Algorithm: Method or algorithm by virtue of which an Artificial Neural Network develops a representation of the information present in the learning examples, by modification of the weights.
Neuron Model: The computation of an artificial neuron, expressed as a function of its input and its weight vector and other local information.
Weight: A free parameter of an Artificial Neural Network, that can be modified through the action of a Learning Algorithm to obtain desired responses to certain input stimuli.