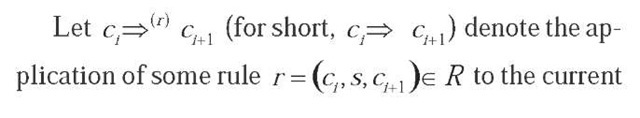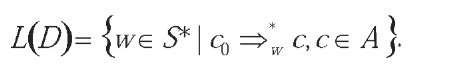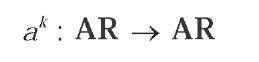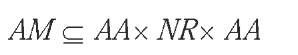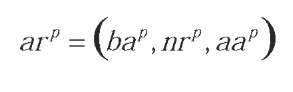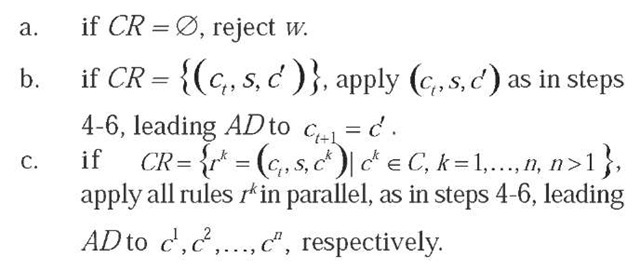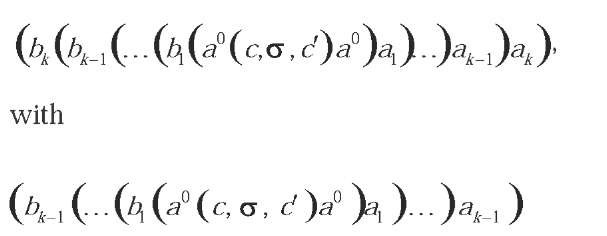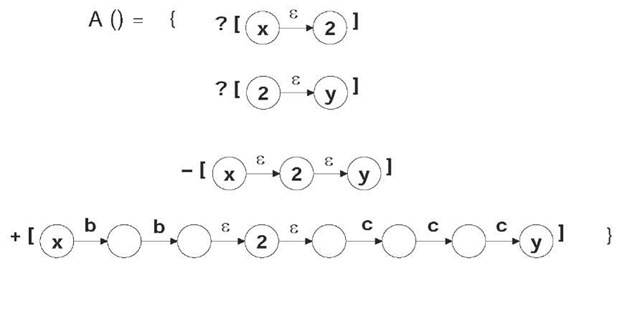INTRODUCTION
Before the advent of software engineering, the lack of memory space in computers and the absence of established programming methodologies led early programmers to use self-modification as a regular coding strategy.
Although unavoidable and valuable for that class of software, solutions using self-modification proved inadequate while programs grew in size and complexity, and security and reliability became major requirements.
Software engineering, in the 70′s, almost led to the vanishing of self-modifying software, whose occurrence was afterwards limited to small low-level machine-language programs with very special requirements.
Nevertheless, recent research developed in this area, and the modern needs for powerful and effective ways to represent and handle complex phenomena in high-technology computers are leading self-modification to be considered again as an implementation choice in several situations.
Artificial intelligence strongly contributed for this scenario by developing and applying non-conventional approaches, e.g. heuristics, knowledge representation and handling, inference methods, evolving software/ hardware, genetic algorithms, neural networks, fuzzy systems, expert systems, machine learning, etc.
In this publication, another alternative is proposed for developing Artificial Intelligence applications: the use of adaptive devices, a special class of abstractions whose practical application in the solution of current problems is called Adaptive Technology.
The behavior of adaptive devices is defined by a dynamic set of rules. In this case, knowledge may be represented, stored and handled within that set of rules by adding and removing rules that represent the addition or elimination of the information they represent.
Because of the explicit way adopted for representing and acquiring knowledge, adaptivity provides a very simple abstraction for the implementation of artificial learning mechanisms: knowledge may be comfortably gathered by inserting and removing rules, and handled by tracking the evolution of the set of rules and by interpreting the collected information as the representation of the knowledge encoded in the rule set.
MAIN FOCUS OF THIS ARTICLE
This article provides concepts and foundations on adaptivity and adaptive technology, gives a general formulation for adaptive abstractions in use and indicates their main applications.
It shows how rule-driven devices may turn into adaptive devices to be applied in learning systems modeling, and introduces a recently formulated kind of adaptive abstractions having adaptive subjacent devices. This novel feature may be valuable for implementing meta-learning, since it enables adaptive devices to change dynamically the way they modify their own set of defining rules.
A significant amount of information concerning adaptivity and related subjects may be found at the (LTA Web site).
BACKGROUND
This section summarizes the foundations of adaptivity and establishes a general formulation for adaptive rule-driven devices (Neto, 2001), non-adaptivity being the only restriction imposed to the subjacent device.
Some theoretical background is desirable for the study and research on adaptivity and Adaptive Technology: formal languages, grammars, automata, computation models, rule-driven abstractions and related subjects.
Nevertheless, either for programming purposes or for an initial contact with the theme, it may be unprob-lematic to catch the basics of adaptivity even having no prior expertise with computer-theoretical subjects.
In adaptive abstractions, adaptivity may be achieved by attaching adaptive actions to selected rules chosen from the rule set defining some subjacent non-adaptive device.
Adaptive actions enable adaptive devices to dynamically change their behavior without external help, by modifying their own set of defining rules whenever their subjacent rule is executed.
For practical reasons, up to two adaptive actions are allowed: one to be performed prior to the execution of its underlying rule, and the other, after it.
An adaptive device behavesjust as it were piecewise non-adaptive: starting with the configuration ofits initial underlying device, it iterates the following two steps, until reaching some well-defined final configuration:
• While no adaptive action is executed, run the underlying device;
• Modify the set of rules defining the device by executing an adaptive action.
Rule-Driven Devices
A rule-driven device is any formal abstraction whose behavior is described by a rule set that maps each possible configuration of the device into a corresponding next one.
A device is deterministicwhen, for any configuration and any input, a single next configuration is possible. Otherwise, it is said non-deterministic.
Non-deterministic devices allow multiple valid possibilities for each move, and require backtracking, so deterministic equivalents are usually preferable in practice.
Assume that:
• D is some rule-driven device, defined as
D =(C, R, S, c0, A).
• C is its set of possible configurations.
• R c Cx(S ^{e })x C is the set of rules describing its behavior, where e denotes empty stimulus, representing no events at all.
• S is its set of valid input stimuli.
• c0 e C is its initial configuration.
• A c C is its set of final configurations.
Successive applications of rules in response to a stream we S * of input stimuli, starting from the initial configuration c0 and leading to some final configuration c e A is denoted c0 c (The star postfix operator in the formulae denotes the Kleene closure: its preceding element may be re-instantiated or reapplied an arbitrary number of times).
We say that D defines a sentence w if, and only if, cjj c holds for some c e A. The collection L(D) of all such sentences is called the language defined by D:
Adaptive (Rule-Driven) Devices
An adaptive rule-driven device AD = (ND0, AM) associates an initial subjacent rule-driven device ND0 = (C, NR0, S, c0, A), to some adaptive mechanism AM, that can dynamically change its behavior by modifying its defining rules.
That is accomplished by executing non-null adaptive actions chosen from a set AA of adaptive actions, which includes the null adaptive action a0.
A built-in counter t starts at 0 and is self-incremented upon any adaptive actions’ execution. Let X denote the value of X after j executions of adaptive actions by AD.
Adaptive actions in AA call functions that map AD current set ARt of adaptive rules into AR+1 by inserting to and removing adaptive rules ar from AM.
Let AR be the set of all possible sets of adaptive rules for AD. Any ak e A maps the current set of rules ARt eAR into ARt +1eAR:
AMassociates to each rule nrp e NRof ADunderlying device ND a pair of adaptive actions bap, aap e AA:
Notation
When writing elementary adaptive actions,?[ar], + [ar] and – [ar]respectively denote searching, inserting and eliminating adaptive rules that follow template ar.
Note that ar may contain references to parameters, variables and generators, in order to allow cross-referencing among elementary adaptive actions inside an adaptive function.
Given an underlying rule nrp e NR, we define an adaptive rule arp e AM as:
For each AD move, AM applies some arp in three steps:
a. execution of adaptive action bap before applying the subjacent rule nrp;
b. application of the underlying non-adaptive rule nrp;
c. execution of adaptive action aap.
The following algorithm sketches the overall operation of AD:
1. Initialize c0, w;
2. If w is exhausted, go to 7 else get next event s;
3. For the current configuration c, determine the set CR of ^-compatible rules;
4. If bap = a0,go to 2, else apply first baP. If rule aF were removed by bap, go to 3 aborting arp, else AD reached an intermediate configuration, then go to 2.
5. Apply nF to the current (intermediate) configuration, yielding a new intermediate configuration;
6. Apply asp, yielding the next (stable) configuration for AD; go to 2
7. If some ct+1 e F was reached, then AD accepts w, otherwise AD rejects w; stop.
Hierarchical Multi-Level Adaptive Devices
Let us define a more elaborated adaptive device by generalizing the definition above. Call non-adaptive devices level-0 devices; define level-1 devices those having subjacent level-0 devices, to each of whose rules a pair of level-1 adaptive actions are attached.
Let the subjacent device be some level-k adaptive device. One may construct a level-(k+1) device attaching a pair of level-(k+1) adaptive actions to each of its rules. This is the induction step for the definition of hierarchically structured multi-level adaptive devices.
Besides the set of rules defining the subj acent level-k device, for k > 0, adaptive functions’ subjacent device performs at its own level, which may use level-(k+1) adaptive actions to modify the behavior of level-k adaptive functions.
So, for k > 0, level-(k+1) devices can change the way their subjacent level-k devices modify themselves. That also holds for k = 1, since even for k = 0 the (empty) set of adaptive functions still exists.
Notation
The absence of adaptive actions in non-adaptive rules nr is explicitly expressed by stating all level-0 rules r0 in the form (a0 nr a0). Therefore, level-k rules rk take the general format (bk rk-1 ak), with both bkand ak level-k adaptive actions for any adaptive level k > 0.
So, level-k adaptive devices have all their defining rules stated in the standard form
representing one of the rules defining the subjacent level-(k – 1) adaptive device.
Hence, level-i adaptive actions can modify both the set of level-i adaptive rules and the set of elementary adaptive actions defining level-(i – 1) adaptive functions.
A SIMPLE ILLUSTRATIVE EXAMPLE
In the following example, graphical notation is used for clarity and conciseness. When drawing automata, (as usual) circles represent states; double-line circles indicate final states; arrows indicate transitions; labels on the arrows indicate tokens consumed by the transition and (optionally) an associated adaptive action. When representing adaptive functions, automata fragments in brackets stand for a group of transitions to be added (+) or removed (-) when the adaptive action is applied.
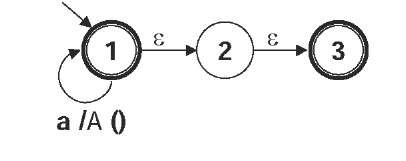
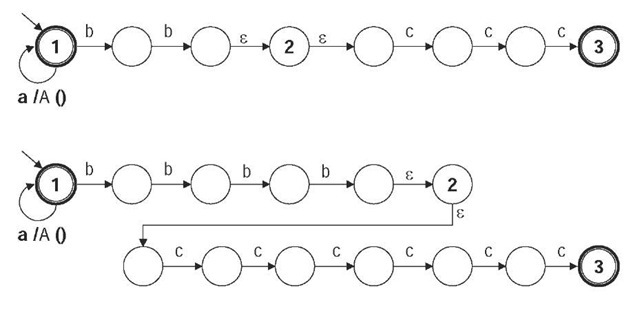
Figure 1 shows the starting shape of an adaptive automaton that accepts anb2nc3n, n>0. At state 1, it includes a transition consuming a, which performs adaptive action A( ).
Figure 2 defines how A() operate:
Figure 1. Initial configuration of the illustrative adaptive automaton
Figure 2. Adaptive function A ( )
• Using state 2 as reference, eliminate empty transitions using states x and y
• Add a sequence starting at x, with two transitions consuming b
• Append the sequence of two empty transitions sharing state 2
Append a sequence with three transitions consuming c, ending at y.
Figure 3 shows the first two shape changes of this automaton after consuming the two first symbols a (at state 1 ) in sentence a2b4c6. In its last shape, the automaton trivially consumes the remaining b4c6, and does not change any more.
There are many other examples of adaptive devices in the references. This almost trivial and intuitive case was shown here for illustration purposes only.
Knowledge Representation
The preceding example illustrates how adaptive devices use the set of rules as their only element for representing and handling knowledge.
A rule (here, a transition) may handle parametric information in its components (here, the transition’s origin and destination states, the token labeling the transition, the adaptive function it calls, etc.).
Rules may be combined together in order to represent some non-elementary information (here, the sequences of transitions consuming tokens “b” and “c” keep track of the value of n in each particular sentence). This way, rules and their components may work and may be interpreted as low-level elements of knowledge.
Although being impossible to impose rules on how to represent and handle knowledge in systems repre sented with adaptive devices, the details of the learning process may be chosen according to the particular needs of each system being modeled.
Figure 3. Configurations of the adaptive automaton after executing A () once and twice
In practice, the learning behavior of an adaptive device may be identified and measured by tracking the progress of the set of rules during its operation and interpreting the dynamics of its changes.
In the above example, when transitions are added to the automaton by executing adaptive action A ( ), one may interpret the length of the sequence of transitions consuming “b” (or “c”) as a manifestation ofthe knowledge that is being gathered by the adaptive automaton on the value of n (its exact value becomes available after the sub-string of tokens “a” is consumed).
FUTURE TRENDS
Adaptive abstractions represent a significant theoretical advance in Computer Science, by introducing and exploring powerful non-classical concepts such as: time-varying behavior, autonomously dynamic rule sets, multi-level hierarchy, static and dynamic adaptive actions.
Those concepts allow establishing a modeling style, proper for describing complex learning systems, for efficiently solving traditionally hard problems, for dealing with self-modifying learning methods, and for providing computer languages and environments for comfortable elaboration of quality programs with dynamically-variant behavior.
All those features are vital for conceiving, modeling, designing and implementing applications in Artificial Intelligence, which benefits from adaptivity while expressing traditionally difficult-to-describe Artificial Intelligence facts.
Listed below are features Adaptive Technology offers to several fields of Computation, especially to Artificial Intelligence-related ones, indicating their main impacts and applications.
• Adaptive Technology provides a true computation model, constructed around formal foundations. Most Artificial Intelligence techniques in use are very hard to express and follow since the connection between elements of the models and information they represent is often implicit, so their operation reasoning is difficult for a human to track and plan. Adaptive rule-driven devices concentrate all stored knowledge in their rules, and the whole logic that handles such information, in their adaptive actions. Such properties open for Artificial Intelligence the possibility to observe, understand and control adaptive-device-modeled phenomena. By following and interpreting how and why changes occur in the device set of rules, and by tracking semantics of adaptive actions, one can infer the reasoning of the model reactions to its input.
• Adaptive devices have enough processing power to model complex computations. In (Neto, 2000) some well-succeeded use cases are shown with simple and efficient adaptive devices used instead of complex traditional formulations.
• Adaptive Devices are Turing Machine-equivalent computation models that may be used in the construction of single-notation full specifications of programming languages, including lexical, syntactical, context-dependent static-semantic issues, language built-in features such as arithmetic operations, libraries, semantics, code generation and optimization, run-time code interpreting, etc.
• Adaptive devices are well suited for representing complex languages, including idioms. Natural language particularly require several features to be expressed and handled, as word inflexions, orthography, multiple syntax forms, phrase ordering, ellipsis, permutation, ambiguities, anaphora and others. A few simple techniques allow adaptive devices to deal with such elements, strongly simplifying the effort of representing and processing them. Applications are wide, including machine translation, data mining, text-voice and voice-text conversion, etc.
• Computer art is another fascinating potential application of adaptive devices. Music and other artistic expressions are forms of human language. Given some language descriptions, computers can capture human skills and automatically generate interesting outputs. Well-succeeded experiments were carried out in the field of music, with excellent results (Basseto, 1999).
• Decision-taking systems may use Adaptive Decision Tables and Trees for constructing intelligent systems that accept training patterns, learn how to classify them, and therefore, classify unknown patterns. Well-succeeded experiments include: classifying geometric patterns, decoding sign languages, locating patterns in images, generating diagnoses from symptoms and medical data, etc.
• Language inference uses Adaptive Devices to generate formal descriptions of languages from samples, by identifying and collecting structural information and generalizing on the evidence of repetitive or recursive constructs (Matsuno, 2006).
• Adaptive Devices can be used for learning purposes by storing as rules the gathered information on some monitored phenomenon. In educational systems, the behavior of both students and trainers can be inferred and used to decide how to proceed.
• One can construct Adaptive Devices whose underlying abstraction is a computer language. Statements in such languages may be considered as rules defining behavior of a program. By attaching adaptive rules to statements, the program becomes self-modifiable. Adaptive languages are needed for adaptive applications to be expressed naturally. For adaptivity to become a true programming style, techniques and methods must be developed to construct good adaptive software, since adaptive applications developed so far were usually produced in strict ad-hoc way.
CONCLUSION
Adaptive Technology concerns techniques, methods and subjects referring to actual application of adaptivity.
Adaptive automata (Neto, 1994) were first proposed for practical representation of context-sensitive languages (Rubinstein, 1995). Adaptive grammars (Iwai, 2000) were employed as its generative counterpart (Burshteyn, 1990), (Christiansen, 1990), (Cabasino, 1992), (Shutt, 1993), (Jackson, 2006).
For specification and analysis of real time reactive systems, works were developed based on adaptive versions of statecharts (Almeida Jr., 1995), (Santos, 1997). An interesting confirmation of power and usability of adaptive devices for modeling complex systems (Neto, 2000) was the successful use of Adaptive Markov Chains in a computer music-generating device (Basseto, 1999).
Adaptive Decision Tables (Neto, 2001) and Adaptive Decision Trees (Pistori, 2006) are nowadays being experimented in decision-taking applications.
Experiments have been reported that explore the potential of adaptive devices for constructing language inference systems (Neto, 1998), (Matsuno, 2006).
An important area in which adaptive devices shows its strength is the specification and processing of natural languages (Neto, 2003). Many other results are being achieved while representing syntactical context-dependencies of natural language.
Simulation and modeling of intelligent systems are other concrete applications of adaptive formalisms, as illustrated in the description of the control mechanism of an intelligent autonomous vehicle which collects information from its environment and builds maps for navigation.
Many other applications for adaptive devices are possible in several fields.
KEY TERMS
Adaptivity: Property exhibited by structures that dynamically and autonomously change their own behavior in response to input stimuli.
Adaptive Computation Model: Turing-powerful abstraction that mimic the behavior of potentially selfmodifying complex systems.
Adaptive Device: Structure with dynamic behavior, with some subjacent device and an adaptive mechanism.
Adaptive Functions andAdaptiveActions: Adaptive actions are calls to adaptive functions, which can determine changes to perform on its layer’s rule set and on their immediately subjacent layer’s adaptive functions.
Adaptive Mechanism: Alteration discipline associated to an adaptive device’s rule set that change the behavior of its subjacent device by performing adaptive actions.
Adaptive Rule-Driven Device: Adaptive device whose behavior is defined by a dynamically changing set of rules, e.g. adaptive automata, adaptive grammars, etc.
Context-Dependency: Reinterpretation of terms, due to conditions occurring elsewhere in a sentence, e.g. agreement rules in English, type-checking in Pascal.
Context-Sensitive (-Dependent) Formalism: Abstraction capable of representing Chomsky type-1 or type-0 languages. Adaptive Automata and Adaptive Context-free Grammars are well suited to express such languages.
Hierarchical (Multilevel) Adaptive Device: Stratified adaptive structures whose involving layer’s adaptive actions can modify both its own layer’s rules and its underlying layer’s adaptive functions.
Subjacent (or Underlying) Device: Any device used as basis to formulate adaptive devices. The innermost of a multilevel subjacent device must be non-adaptive.