INTRODUCTION
This chapter spans topics from such important areas as Artificial Intelligence, Computational Geometry and Biometric Technologies. The primary focus is on the proposed Adaptive Computation Paradigm and its applications to surface modeling and biometric processing.
Availability of much more affordable storage and high resolution image capturing devices have contributed significantly over the past few years to accumulating very large datasets of collected data (such as GIS maps, biometric samples, videos etc.). On the other hand, it also created significant challenges driven by the higher than ever volumes and the complexity of the data, that can no longer be resolved through acquisition of more memory, faster processors or optimization of existing algorithms. These developments justified the need for radically new concepts for massive data storage, processing and visualization. To address this need, the current chapter presents the original methodology based on the paradigm of the Adaptive Geometric Computing. The methodology enables storing complex data in a compact form, providing efficient access to it, preserving high level of details and visualizing dynamic changes in a smooth and continuous manner.
The first part of the chapter discusses adaptive algorithms in real-time visualization, specifically in GIS (Geographic Information Systems) applications. Data structures such as Real-time Optimally Adaptive Mesh (ROAM) and Progressive Mesh (PM) are briefly surveyed. The adaptive method Adaptive Spatial Memory (ASM), developed by R. Apu and M. Gavrilova, is then introduced. This method allows fast and efficient visualization of complex data sets representing terrains, landscapes and Digital Elevation Models (DEM). Its advantages are briefly discussed.
The second part of the chapter presents application of adaptive computation paradigm and evolutionary computing to missile simulation. As a result, patterns of complex behavior can be developed and analyzed.
The final part of the chapter marries a concept of adaptive computation and topology-based techniques and discusses their application to challenging area of biometric computing.
BACKGROUND
For a long time, researchers were pressed with questions on how to model real-world objects (such as terrain, facial structure or particle system) realistically, while at the same time preserving rendering efficiency and space. As a solution, grid, mesh, TIN, Delaunay triangulation-based and other methods for model representation were developed over the last two decades. Most of these are static methods, not suitable for rendering dynamic scenes or preserving higher level of details.
In 1997, first methods for dynamic model representation: Real-time Optimally Adapting Mesh (ROAM) (Duchaineauy et. al., 1997, Lindstrom and Koller, 1996) and Progressive Mesh (PM) (Hoppe, 1997) were developed. Various methods have been proposed to reduce a fine mesh into an optimized representation so that the optimized mesh contains less primitives and yields maximum detail. However, this approach had two major limitations. Firstly, the cost of optimization is very expensive (several minutes to optimize one medium sized mesh). Secondly, the generated non-uniform mesh is still static. As a result, it yields poor quality when only a small part of the mesh is being observed. Thus, even with the further improvements, these methods were not capable of dealing with large amount of complex data or significantly varied level of details. They have soon were replaced by a different computational model for rendering geometric meshes (Li Sheng et. al. 2003, Shafae and Pajarola, 2003). The model employs a continuous refinement criteria based on an error metric to optimally adapt to a more accurate representation. Therefore, given a mesh representation and a small change in the viewpoint, the optimized mesh for the next viewpoint can be computed by refining the existing mesh.
ADAPTIVE GEOMETRIC COMPUTING
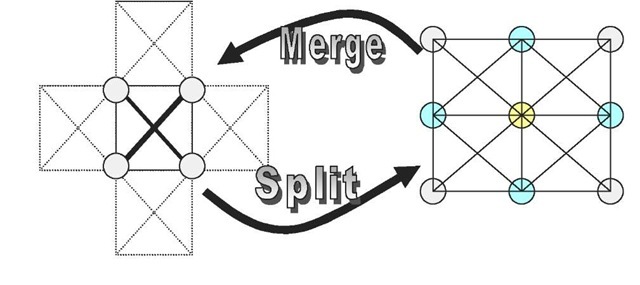
This chapter presents Adaptive Multi-Resolution Technique for real-time terrain visualization utilizing a clever way of optimizing mesh dynamically for smooth and continuous visualization with a very high efficiency (frame rate) (Apu and Gavrilova (2005) (2007)). Our method is characterized by the efficient representation of massive underlying terrain, utilizes efficient transition between detail levels, and achieves frame rate constancy ensuring visual continuity. At the core of the method is adaptive processing: a formalized hierarchical representation that exploits the subsequent refinement principal. This allows us a full control over the complexity of the feature space. An error metric is assigned by a higher level process where obj ects (or features) are initially classified into different labels. Thus, this adaptive method is highly useful for feature space representation. In 2006, Gavrilova and Apu showed that such methods can act as a powerful tool not only for terrain rendering, but also for motion planning and adaptive simulations (Apu and Gavrilova, 2006). They introduced Adaptive Spatial Memory (ASM) model that utilizes adaptive approach for real-time online algorithm for multi-agent collaborative motion planning. They have demonstrate that the powerful notion of adaptive computation can be applied to perception and understanding of space. Extension of this method for 3D motion planning as part of collaborative research with Prof. I. Kolingerova group has been reported to be significantly more efficient than conventional methods (Broz et.al., 2007).
We first move to discuss evolutionary computing. We demonstrate the power of adaptive computation by developing and applying adaptive computational model to missile simulation (Apu and Gavrilova, 2006). The developed adaptive algorithms described above have a property that spatial memory units can form, refine and collapse to simulate learning, adapting and responding to stimuli. The result is a complex multi-agent learning algorithm that clearly demonstrates organic behaviors such as sense of territory, trails, tracks etc. observed in flocks/herds of wild animals and insects. This gives a motivation to explore the mechanism in application to swarm behavior modeling.
Swarm Intelligence (SI) is the property of a system whereby the collective behaviors of unsophisticated agents interacting locally with their environment cause coherent functional global patterns to emerge (Bo-nabeau, 1999). Swarm intelligence provides a basis for exploration of a collective (distributed) behavior of a group of agents without centralized control or the provision of a global model. Agents in such system have limited perception (or intelligence) and cannot individually carry out the complex tasks. According to Bonebeau, by regulating the behavior of the agents in the swarm, one can demonstrate emergent behavior and intelligence as a collective phenomenon. Although the swarming phenomenon is largely observed in biological organisms such as an ant colony or a flock of birds, it is recently being used to simulate complex dynamic systems focused towards accomplishing a well-defined objective (Kennedy, 2001, Raupp ans Thalmann, 2001).
Figure 1. Split and merge operations in ASM model
Let us now investigate application of the adaptive computational paradigm and swarm intelligence concept to missile behavior simulation (Apu and Gavrilova, 2006). First of all, let us note that complex strategic behavior can be observed by means of a task oriented artificial evolutionary process in which behaviors of individual missiles are described in surprising simplicity. Secondly, the global effectiveness and behavior of the missile swarm is relatively unaffected by disruption or destruction of individual units. From a strategic point of view, this adaptive behavior is a strongly desired property in military applications, which motivates our interest in applying it to missile simulation. Note that this problem was chosen as it presents a complex challenge for which an optimum solution is very hard to obtain using traditional methods. The dynamic and competitive relationship between missiles and turrets makes it extremely difficult to model using a deterministic approach. It should also be noted that the problem has an easy evaluation metric that allows determining fitness values precisely.
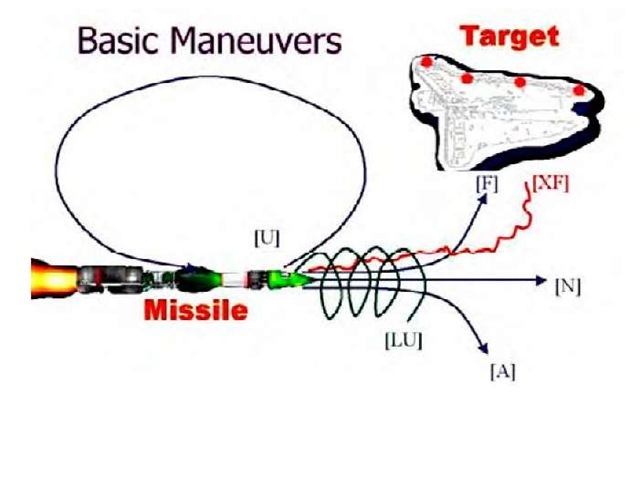
Now, let us summarize the idea of evolutionary optimization by applying genetic algorithm to evolve the missile genotype. We are particularly interested in observing the evolution of complex 3D formations and tactical strategies that the swarm learns to maximize their effectiveness during an attack simulation run. The simulation is based on attack, evasion and defense. While the missile sets strategy to strike the target, the battle ship prepares to shoot down as many missiles as possible (Figure 2 illustrates the basic missile maneuvers). Each attempt to destroy the target is called an attack simulation run. Its effectiveness equals to the number of missiles hitting the target. Therefore the outcome of the simulation is easily quantifiable. On the other hand, the interaction between missiles and the battleship is complex and nontrivial. As a result, war strategies may emerge in which a local penalty (i.e. sacrificing a missile) can optimize global efficiency (i.e. deception strategy). The simplest form of information known to each missile is its position and orientation and the location of the target. This information is augmented with information about missile neighborhood and environment, which influences missile navigation pattern. For actual missile behavior simulation, we use strategy based on the modified version of Boids flocking technique.
Figure 2. Basic maneuvers for a missile using the Gene String
We have just outlined the necessary set of actions to reach the target or interact with the environment. This is the basic building block of missile navigation. The gene string is another important part that reflects the complexity with which such courses of action could be chosen. It contains a unique combination of maneuvers (such as attack, evasion, etc.) that evolve to create complex combined intelligence. We describe the fitness of the missile gene in terms of collective performance. After investigating various possibilities, we developed and used a two dimensional adaptive fitness function to evolve the missile strains in one evolutionary system. Details on this approach can be found in (Apu and Gavrilova, 2006).
After extensive experimentation, we have found many interesting characteristics, such as geometric attack formation and organic behaviors observed among swarms in addition to the highly anticipated strategies such as simultaneous attack, deception, retreat and other strategies (see Figure 3). We also examined the adaptability by randomizing the simulation coordinates, distance, initial formation, attack rate, and other parameters of missiles and measured the mean and variance of the fitness function. Results have shown that many of the genotypes that evolved are highly adaptive to the environment.
We have just reviewed the application of the adaptive computational paradigm to swarm intelligence and briefly described the efficient tactical swarm simulation method (Apu and Gavrilova 2006). The results clearly demonstrate that the swarm is able to develop complex strategy through the evolutionary process of genotype mutation. This contribution among other works on adaptive computational intelligence will be profiled in detail in the upcoming topic as part of Springer-Verlag topic series on Computational Intelligence (Gavrilova, 2007).
As stated in the introduction, adaptive computation is based on a variable complexity level of detail paradigm, where a physical phenomenon can be simulated by the continuous process of local adaptation of spatial complexity. As presented by M. Gavrilova in Plenary Lecture at 3IA Eurographics Conference, France in 2006, the adaptive paradigm is a powerful computational model that can also be applied to vast area of biometric research. This section therefore reviews methods and techniques based on adaptive geometric methods in application to biometric problems. It emphasizes advantages that intelligent approach to geometric computing brings to the area of complex biometric data processing (Gavrilova 2007).
In information technology, biometrics refers to a study of physical and behavioral characteristics with the purpose of person identification (Yanushkevich, Gavrilova, Wang and Srihari, 2007). In recent years, the area of biometrics has witnessed a tremendous growth, partly as a result of a pressing need for increased security, and partly as a response to the new technological advances that are literally changing the way we live. Availability of much more affordable storage and the high resolution image biometric capturing devices have contributed to accumulating very large datasets of biometric data. In the earlier sections, we have studied the background of the adaptive mesh generation. Let us now look at the background research in topology-based data structures, and its application to biometric research. This information is highly relevant to goals of modeling and visualizing complex biometric data. At the same time as adaptive methodology was developing in GIS, interest to topology-based data structures, such as Voronoi diagrams and Delaunay triangulations, has grown significantly. Some preliminary results on utilization of these topology-based data structures in biometric began to appear. For instance, research on image processing using Voronoi diagrams was presented in (Liang and Asano, 2004, Asano, 2006), studies of utilizing Voronoi diagram for fingerprint synthesis were conducted by (Bebis et. al., 1999, Capelli et. al. 2002), and various surveys of methods for modeling of human faces using triangular mesh appeared in (Wen and Huang, 2004, Li and Jain, 2005, Wayman et. al. 2005). Some interesting results were recently obtained in the BTLab, University of Calgary, through the development of topology-based feature extraction algorithms for fingerprint matching (Wang et. al. 2006, 2007, illustration is found in Figure 4), 3D facial expression modeling (Luo et. al. 2006) and iris synthesis (Wecker et. al. 2005). A comprehensive review of topology-based approaches in biometric modeling and synthesis can be found in recent topic chapter on the subject (Gavrilova, 2007).
In this chapter, we propose to manage the challenges arising from large volumes of complex biometric data through the innovative utilization of the adaptive paradigm. We suggest combination of topology-based and hierarchy based methodology to store and search for biometric data, as well as to optimize such representation based on the data access and usage. Namely, retrieval of the data, or creating real-time visualization can be based on the dynamic patter of data usage (how often, what type of data, how much details, etc.), recorded and analyzed in the process of the biometric system being used for recognition and identification purposes.
Figure 3. Complex formation and attack patterns evolved
Figure 4. Delaunay triangulation based technique for fingerprint matching
In addition to using this information for optimized data representation and retrieval, we also propose to incorporate intelligent learning techniques to predict most likely patters of the system usage and to represent and organize data accordingly.
On a practical side, to achieve our goal, we propose a novel way to represent complex biometric data through the organization of the data in a hierarchical tree-like structure. Such organization is similar in principle to the Adaptive Memory Subdivision (AMS), capable of representing and retrieving varies amount of information and level of detail that needs to be represented. Spatial quad-tree is used to hold the information about the system, as well as the instructions on how to process this information. Expansion is realized through the spatial subdivision technique that refines the data and increases level of details, and the collapsing is realized through the merge operation that simplifies the data representation and makes it more compact. The greedy strategy is used to optimally adapt to the best representation based on the user requirements, amount of available data and resources, required resolution and so on. This powerful technique enables us to achieve the goal of compact biometric data representation, that allows for instance to efficiently store minor details of the modeled face (e.g. scars, wrinkles) or detailed patterns of the iris.
FUTURE TRENDS
In addition to data representation, adaptive technique can be highly useful in biometric feature extraction with the purpose of fast and reliable retrieval and matching of the biometric data, and in implementing dynamic changes to the model. The methodology has a high potential of becoming one of the key approaches in biometric data modeling and synthesis.
CONCLUSION
The chapter reviewed the adaptive computational paradigm in application to surface modeling, evolutionary computing and biometric research. Some of the key future developments in the upcoming years will undoubtedly highlight the area, inspiring new generations of intelligent biometric systems with adaptive behavior.
KEY TERMS
Adaptive Geometric Model (AGM): A new approach to geometric computing utilizing adaptive computation paradigm. The model employs a continuous refinement criteria based on an error metric to optimally adapt to a more accurate representation.
Adaptive Multi-Resolution Technique (AMRT): For real-time terrain visualization is a method that utilizes a clever way of optimizing mesh dynamically for smooth and continuous visualization with a high efficiency.
Adaptive Spatial Memory (ASM): A hybrid method based on the combination of traditional hierarchical tree structure with the concept of expanding or collapsing tree nodes.
Biometric Technology (BT): An area of study of physical and behavioral characteristics with the purpose of person authentication and identification.
Delaunay Triangulation (DT): A computational geometry data structure dual to Voronoi diagram.
Evolutionary Paradigm (EP): The collective name for a number of problem solving methods utilizing principles of biological evolution, such as natural selection and genetic inheritance.
Swarm Intelligence (SI): The property of a system whereby the collective behaviors of unsophisticated agents interacting locally with their environment cause coherent functional global patterns to emerge.
Topology-Based Techniques (TBT): A group of methods using geometric properties of a set of objects in the space and their proximity
Voronoi Diagram (VD): A fundamental computational geometry data structure that stores topological information for a set of objects.