Quantitative Aspects of Clinical Decision Making Part 3

Medical Decision Analysis

Clearly, there is more to clinical decision making than simply collecting numbers that measure treatment effects. Reports of treatment effects in randomized, controlled trials are important starting points that help determine whether a treatment has merit in its own right, but the actual decision whether to offer a given patient a particular treatment is complex and must take into account each patient’s specific clinical circumstances and individual wishes. For example, if the patient has significant comorbidity that would result in an especially high risk of perioperative complications, surgical therapy might not be the best choice. Even if the patient is well enough to undergo operation, individual preferences and values must be taken into account: the patient might be strongly averse to the immediate risks posed by surgery or might lack the resources to pay for the procedure.

The threshold model of decision making

At the conclusion of every history and physical examination, the clinician must choose one of three options: to treat, to observe, or to obtain more information. The optimal approach to making this choice starts with the assumption that the physician will seek more information (i.e., order diagnostic tests) only if the results may alter the treatment decision. Although occasional exceptions are easily justified, this rule is a good guiding principle for a lean style of practice. It is also the central assumption behind the threshold model of decision making.

When a diagnosis is uncertain, the decision whether to start treatment depends on the probability of the diagnosis. If the probability is 0, no one would start treatment; if the probability is 1, everyone would start treatment. Therefore, there must be a probability between 0 and 1 at which a physician would have no preference between treating and not treating. This probability is called the treatment threshold probability.

The treatment threshold probability is a key to solving the important decision-making problem of whether to treat, to observe, or to obtain more information. The most elegant way of obtaining the treatment threshold probability is to construct a decision tree that represents the choice between starting treatment and withholding treatment [see Figure 2]. In a decision tree, decisions are represented by squares (decision nodes), and the chance events that follow a decision are represented by circles (chance nodes). The probabilities of the events after a chance node must total 1.0. A terminal node (represented by a rectangle enclosing the name of the state) represents a state in which there are no subsequent chance events. Each terminal node has a value, which is a measure of the outcome associated with the event.

In a decision tree for starting or withholding treatment, each branch of the two chance nodes ends in a terminal node whose value is the utility (U) for being in the state specified. For example, U[D+, Rx+] is the utility for having the disease (D) and being treated for it, which one could calculate by representing that state as a tree with chance nodes and terminal nodes. To obtain the treatment threshold probability, one sets the expected utility of treatment at a value equal to the value for the expected utility of no treatment and then solves for the probability of disease. The general solution to the equation is as follows:

where harm is the net utility of being treated when disease is absent (U[D-, Rx+] – U[D-, Rx-]) and benefit is the net utility of being treated when disease is present (U[D+, Rx+] – U[D+, Rx-]). This relationship between harms and benefits of treatment is fundamental to solving the common decision problem of deciding about treatment when the diagnosis is not known with certainty. Because the treatment threshold depends on the benefits and harms of the treatment, it will vary from treatment to treatment. When the benefits of a treatment exceed harms, which is usually the case, the treatment threshold probability must be less than 0.50.

To make the choice between treating, not treating, and ordering tests to obtain additional information, the physician needs to know the range of probabilities of disease within which testing is the preferred action. The probability scale can be divided into three ranges [see Figure 3], one of which is the test range. The first step in defining the test range is to establish the treatment threshold probability. For the next step, we must invoke the principle that the physician should seek more information only if the results might alter the treatment decision. Translated to the threshold model, this principle takes the following form: testing is indicated only if the result of the test might move the probability of disease from one side of the treatment threshold (the do-not-treat side) to the other (the treat side). A physician can use this principle to decide whether to obtain a test in an individual patient. If the patient’s pretest probability is below the treatment threshold and therefore in the do-not-treat zone, the physician should order the test only if the posttest probability of disease after a positive test result would be higher than the treatment threshold probability.

To obtain the test range, we must extend this example to a more general solution, which is to use the test’s likelihood ratio and Bayes’ theorem to calculate the pretest probability at which the posttest probability is exactly equal to the treatment threshold probability [see Figure 3]. This probability is called the no treat-test threshold probability. Clearly, if the pretest probability is lower than the no treat-test threshold probability, the test should not be done, because the posttest probability will be lower than the treatment threshold probability (i.e., a positive result will not change the management decision); conversely, if the pretest probability is higher than the no treat-test threshold probability, the test should be done, because the posttest probability will be higher than the treatment threshold probability (i.e., a positive test result would change the management decision from do not treat to treat).

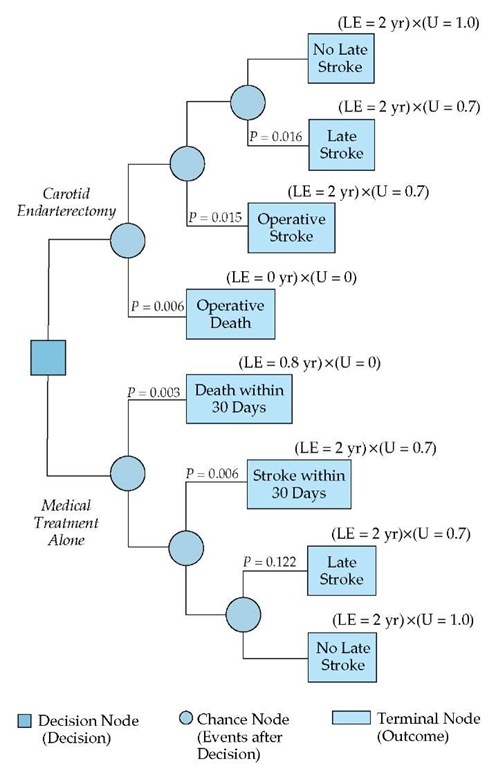
Figure 4 Shown is a decision tree depicting the application of expected-outcome decision analysis to the same patient referred to in Figure 2. (LE—life expectancy; U—utility)

The size of the test range depends on the likelihood ratios reported for the test. If LR- is close to zero and LR+ is much greater than 1.0, the test range will be very wide. In general, the better the test, the larger the test range. If the posttest probability falls within the treat zone, the physician must then decide which treatment to offer. The choice among treatments offers a good opportunity to explore the principles of decision making under conditions of uncertainty.

Measures of expected-outcome decision making: the treatment decision

The purpose of decision analysis is to help with those decisions for which the outcome cannot be foretold (e.g., the decision whether to treat carotid artery stenosis surgically). Even when randomized trial results indicate that one treatment generally gives better results than another, some degree of uncertainty remains: individual patients may still exhibit idiosyncratic outcomes or may experience unusual but serious side effects of treatment. Faced with this uncertainty, most physicians choose the treatment that gives the best results averaged over a large number of patients. In so doing, they become, perhaps unwittingly, what are known as "expected-value decision makers." Expected value is the value of an intervention when the outcomes of that intervention are averaged over many patients. A more general term might be "expected-outcome decision maker," which would denote a physician who chooses the treatment that gives the best outcome when averaged over many patients. This concept is the basis of expected-outcome decision analysis, which is a method of framing a decision problem in terms of the expected outcome of each decision alternative. Thus, in a patient with stable angina, the physician would decide between medical management, coronary angioplasty, and coronary artery bypass surgery by first calculating a patient’s life expectancy, expressed in years in good health, after undergoing each of these treatment options; then, the physicial would choose the treatment with the highest life expectancy.

We can illustrate the application of expected-outcome decision making by returning to the example of the 69-year-old man who has recovered from a hemispheric stroke and has a 75% carotid stenosis. The question to be answered is the same: Should the patient be offered carotid endarterectomy in addition to best medical treatment? The first step is to represent the problem by a decision tree [see Figure 4]. Each of the terminal nodes in this decision tree is associated with a life expectancy, as well as a utility representing the value of life in the outcome state, represented by the terminal node. As noted earlier [see How to Apply Research Results to Patient Care, Measures of Treatment Outcome Adjusted for Quality of Life, above], life expectancy by itself is not a sufficiently precise measure: clearly, 2 years of life after a major stroke is not equivalent to 2 years in perfect health. The decision maker needs a quantitative measure of the patient’s feelings about being in an outcome state. The physician can obtain the patient’s utility for that state by asking the patient to indicate the length of time in perfect health that he would consider equivalent to his life expectancy in a disabled state (e.g., after a major stroke). This technique is called time trade-off. Other techniques used to obtain this utility include linear scaling and the standard reference gamble.

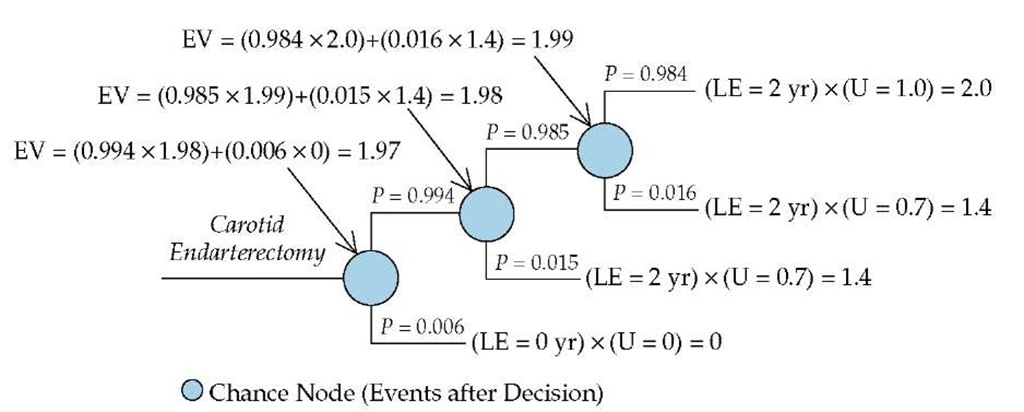
Figure 5 Illustrated is the process of averaging out at a chance node, as applied to the upper (carotid endarterectomy) portion of the decision tree depicted in Figure 2. (EV—expected value; LE—life expectancy; U—utility)

To calculate the expected value of surgical management, the decision maker starts at the chance nodes that are farthest from the decision node (the tips of the branches of the decision tree), multiplies the probability of each event at each chance node by the value of the event, and sums these products over all the events at the chance node. This calculation is known as averaging out at a chance node [see Figure 5]. The value obtained for each chance node by means of this process becomes the outcome measure for the next step, which is to repeat the averaging-out process at the next chance node to the left.

With either therapeutic option—aspirin combined with carotid endarterectomy or continued management with aspirin alone—there is a chance of death within 30 days, stroke within 30 days, or stroke within 2 years [see Figure 4]. As noted [see How to Apply Research Results to Patient Care, Measures of Treatment Effects, above], reliable data on the probabilities of these adverse events are available in the NASCET report.24 To simplify the presentation of the decision analysis, we measure survival only within the 2-year time frame addressed in the NASCET report, and we assume that all late strokes occur at the start of this 2-year period. Further, we assume that a patient would value 2 years of disability resulting from a stroke as equivalent to 17.5 months of healthy life, which means that the utility representing the state of having experienced a major stroke is 0.70.

The decision analysis indicates that the decision maker should prefer surgical treatment to medical treatment. The expected value of carotid endarterectomy for this patient is 1.96 QALY, whereas the expected value of medical treatment is 1.91 QALY. Admittedly, this difference is not very large, indicating a close call, and it is reasonable to ask how high the operative mortality would have to be to make medical treatment the favored approach. Sensitivity analysis, one of the most powerful features of decision analysis, shows that the operative mortality would have to increase considerably before medical treatment would become preferable. The baseline figure for operative mortality in the NASCET report was 0.6%. The sensitivity analysis indicates that medical treatment would have a higher expected value than surgical treatment only if the operative mortality were 3.2% or higher, which might be the case if considerable comorbidity were present or if the surgeon seldom performed carotid endarterectomy. Although most physicians would not have the time or expertise to carry out this decision analysis, storing the appropriate decision tree in a palmtop computer would make it possible to do the decision analysis easily in the office setting, using values specific to the clinical setting and the patient.

Cost-effectiveness analysis

Cost-effectiveness analysis is a method for comparing the impact of expenditures on different health outcomes. Cost-effectiveness analysis assesses the trade-off between added benefit and added cost by examining costs and benefits at the margin (i.e., comparing one intervention with another or with no intervention). The cost-effectiveness of one intervention (A) versus another (B) is calculated as follows:

In the carotid endarterectomy example, the costs would include all costs associated with a subsequent stroke. If we assume that the average lifetime cost associated with carotid endarterec-tomy is $10,000 and the average lifetime cost associated with medical treatment is $8,000, then the cost-effectiveness of surgical treatment, as compared with medical treatment, would be calculated as follows:

One may then ask, is a treatment choice that costs $40,000 for each extra QALY cost-effective? There is no absolute answer to this question. In practice, a physician compares the cost-effectiveness of carotid endarterectomy with that of other interventions. How this information should affect the decision whether to offer surgical treatment to any given patient is an even more difficult question. Indeed, most experts would say that cost-effectiveness is a technique for deciding policies that would apply to many patients. An organization with limited resources would choose policies that prescribe interventions with the lowest cost per added QALY. The organization would not offer interventions that have a high cost relative to the magnitude of the anticipated benefit.

Conclusion

Quantitative approaches to clinical reasoning are still evolving. By combining better evidence from health care research with today’s burgeoning information technology, physicians can apply evidence effectively to individual patient care. As requirements for efficiency and accountability continue to increase, physicians are under more and more pressure to adopt a quantitative, evidence-based approach to patient care. Physicians who can back up their decisions with sound research and sound reasoning will be in a better position to provide their patients with optimal care.