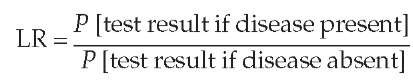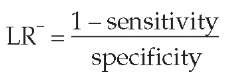Measures of diagnostic test performance and interpretation
Clinically useful measures of diagnostic test performance include sensitivity, specificity, and the likelihood ratio; clinically useful measures of test interpretation include pretest odds, pretest probability, probability after a positive test result, and probability after a negative test result [see Table 3]. Physicians should memorize and internalize the definitions of these terms to avoid becoming muddled when attempting to use information from diagnostic tests in decision making.
In the past, articles usually described the performance of a diagnostic test only in terms of sensitivity and specificity. These familiar terms do not directly describe the effect of a test result on the probability of disease. To correct this shortcoming, many articles now use the likelihood ratio (LR), which is the amount by which the odds of a disease change with new information. This value is calculated as follows:
Because physicians often express test results as either positive or negative, there is a likelihood ratio for a positive test re-sult (LR+) and a likelihood ratio for a negative test result (LR ).
Table 3 Definitions of Clinically Useful Measures of Diagnostic Test Performance and Interpretation
|
Diagnostic Test Result |
Presence or Absence of Disease on a Reference Test (Gold Standard) |
No. of Patients with Given Test Result |
|
|
Present |
Absent |
||
|
Positive |
a |
b |
a + b |
|
Negative |
c |
d |
c + d |
|
Total |
a + c |
b + d |
|
Measures of diagnostic test performance, defined below, are calculated from this table.
The typical approach to evaluation of most diagnostic tests, particularly those with so-called binary outcomes (e.g., a positive or a negative test result, with no other categories), makes use of a 2 x 2 table, as follows:
• Sensitivity: the proportion of people with a disease of interest who are detected by a diagnostic test; calculated as a/(a+c).
• Specificity: the proportion of people who do not have a disease who are correctly identified by a negative result on a diagnostic test; calculated as d/(b+d).
• Likelihood ratio: the amount by which the odds of having a disease change after a test result; calculated as [a/(a+c)]/[b/(b+d)] for a positive test result and as [c/(a+c)]/[d/(b+d)] for a negative test result.
• Pretest probability: the proportion of people with the disorder of interest in a group suspected of having the disorder; calculated as (a+c)/(a+b+c+d).
• Odds: calculated as probability/(1 – probability).
• Probability: calculated as odds/(1+ odds).
• Posttest odds: calculated as pretest odds x likelihood ratio.
• Probability after a positive test: the proportion of people with a positive test result who have the disease of interest; calculated as a/(a+b).
• Probability after a negative test: the proportion of people with a negative test result who have the disease of interest; calculated as c/(c+d).
The formula for the likelihood ratio for a positive test result is as follows:
The formula for the LR for a negative test is as follows:
The likelihood ratio is generally a better descriptor than sensitivity or specificity because it more directly describes the effect of a test result on the odds of disease. The probability after obtaining new information is an application of Bayes’ theorem. The most useful form of Bayes’ theorem for this purpose is the odds ratio format:
Posttest odds = pretest odds x likelihood ratio
This form of Bayes’ theorem illustrates a very powerful concept that clinicians often overlook: new information has meaning only in context. Operationally, the statement means that a physician should never interpret a test result in isolation but should always take into account the individual patient’s pretest probability. Simply stated, the posttest probability after a positive test result will be greater if the pretest index of suspicion was high than if the pretest index of suspicion was low. The most important practical application of this reasoning is to be suspicious when a test result is negative in a patient whose clinical findings strongly point toward a disease—that is, the probability of the disease may still be high, even after the negative test. One should also be suspicious when a test is positive in a patient for whom the likelihood of disease is very low.
The evaluation of suspected pulmonary embolism (PE) is a good example of the practical use of these statistical terms and methods. A 37-year-old woman presents to the emergency department (ED) with pleuritic chest pain and new dyspnea. She has a low-grade fever and has no cough or hemoptysis, but the ED physician believes it necessary to rule out PE. The patient has none of the other known risk factors for PE (e.g., recent surgery or prolonged bed rest, previous deep vein thrombosis [DVT], co-agulopathy, malignancy, pregnancy, and use of oral contraceptives), and physical examination reveals no evidence of DVT. The arterial oxygen tension (PaO2) is 92 mm Hg on room air. The patient is quite distressed. The ED physician orders a chest x-ray and a helical CT scan. The CT scan is interpreted as negative for PE. The resident wishes to explain this result to the patient and then to take the appropriate next steps.
A useful flowchart for working up patients with suspected PE is provided elsewhere [see 1:XVIII Venous Thromboembolism]; however, this chart provides no guidance on how to estimate the clinical probability of PE. It is instructive to examine how the results of a quantitative, evidence-based approach to this patient’s case relate to the recommendations outlined in the flowchart.
The initial step is to estimate the pretest probability of PE by one of two approaches. The first is to use the anchoring and adjustment heuristic. The anchor, or starting point, is the prevalence of PE in adults who present to the ED with pleuritic chest pain. One very careful study found that 21% of such patients (36/173) had a positive pulmonary angiogram.18 The physician should use this 21% initial probability as the starting point (the anchor) for the patient under discussion and adjust it on the basis of the history and the physical examination. As noted, this patient has no predisposing factors for PE and no evidence of DVT, and her Pao is greater than 90 mm Hg. Using this approach, the ED physician concludes that the probability of PE before helical CT is quite low, perhaps 10%.19
The second approach is to use a clinical prediction rule.20 This model places patients into three categories on the basis of clinical findings (typical for PE, atypical for PE, severe PE), the likelihood of alternative diagnoses, and the presence of risk factors for DVT. The prevalence rates of PE in the three categories are 3.4%, 27.8%, and 78.4%, respectively. The algorithm for placing patients into one of the three categories is somewhat complex but is easy to use when represented on the screen of a palmtop computer. Assuming that the ED physician did not identify an alternative diagnosis that seemed more likely than PE, the patient’s pretest probability of PE was 28%, considerably higher than the ED physician’s subjective probability.
With an estimate for the pretest probability of PE, the next step is to obtain the likelihood ratio for a negative helical CT scan. The sensitivity and specificity of the helical CT scan have varied considerably among studies. A recent meta-analysis of studies of diagnostic tests for pulmonary embolism found the likelihood ratio for a positive chest CT scan to be 24.1 (95% CI,12.4 to 46.7). The likelihood ratio for a negative scan was 0.04 (95% CI, 0.03 to 0.06).21
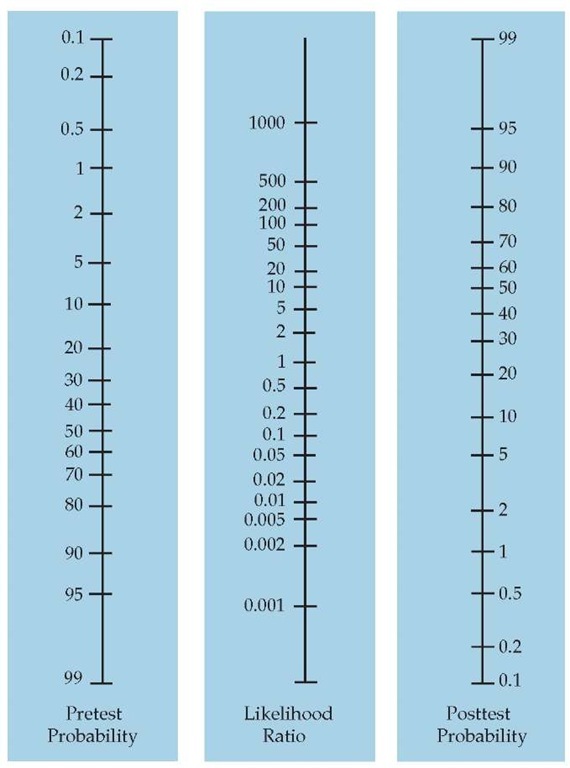
To calculate the posttest odds of PE, the ED physician must combine the patient’s pretest odds with the test’s likelihood ratio by means of the odds ratio format of Bayes’ theorem mentioned earlier (posttest odds = pretest odds x likelihood ratio). An alternative to converting the pretest probability to odds and doing the calculation of posttest odds is to use a nomogram [see Figure 1]. To estimate posttest probability, anchor a straightedge at a pretest probability of 28% (corresponding to the clinical predictive rule’s estimate of pretest probability) in the left-hand column; then pass the straightedge through a likelihood ratio for a negative helical CT scan, 0.04, in the middle column. Read the posttest probability from the right-hand column: about 1.5%. The math for this estimate is as follows, with the 0.28 pretest probability of PE first needing to be converted to pretest odds:
Pretest odds = pretest probability/(1 – pretest probability) = 0.28/(1 – 0.28) = 0.28/0.72 = 0.39
Now, the post-helical CT scan odds of PE for this patient must be determined by multiplying the pretest odds of PE, 0.39, by the likelihood ratio for a negative helical CT, 0.04:
Posttest odds = pretest odds x likelihood ratio = 0.39 x 0.04 = 0.0156
Figure 1 Nomogram for converting pretest probabilities to posttest probabilities when test results are presented as likelihood ratios.
Table 4 Definitions of Clinically Useful Measures of Treatment Effects from Clinical Trials
|
Treatment |
Treatment Outcome |
No. of Patients in Treatment Group |
|
|
Group |
Bad |
Good |
|
|
Experimental |
a |
b |
a +b |
|
Control |
c |
d |
c +d |
|
Total |
a + c |
b + d |
|
Measures of treatment effects when treatment reduces the risk of bad outcomes are calculated from this table.
Like evaluation of diagnostic tests, evaluation of treatment effects often makes use of a 2 x 2 table, as follows:
• Experimental event rate (EER): the rate of an adverse clinical outcome in the experimental group; calculated as a/(a+b).
• Control event rate (CER): the rate of an adverse clinical outcome in the control group; calculated as c/(c+d).
• Absolute risk reduction (ARR): the absolute arithmetic difference in outcome rates between control and experimental groups in a trial; calculated as CER – EER, or [c/(c+d)] – [a/(a+b)].
• Relative risk reduction (RRR): the proportional reduction in the rate of an adverse clinical outcome in the experimental group in comparison with the control group in a trial; calculated as ARR/ CER, or (CER – EER)/CER, or {[c/(c+d)] – [a/(a+b)])/[c/(c+d)].
• Number needed to treat (NNT): the number of patients to whom one would have to give the experimental treatment to prevent one adverse clinical outcome; calculated as 1/ARR, or 1/{[c/(c+d)] – [a/(a+b)]), and reported as a whole number rounded to the next highest integer.
• Odds ratio: the odds that an experimental patient will experience an adverse event relative to the odds that a control subject will experience such an event; calculated as (a/b)/(c/d).
Convert the posttest odds to the posttest probability, as follows:
Posttest probability = posttest odds/(1 + posttest odds) = 0.0156/(1 + 0.0156) = 0.0154
At a posttest probability of PE of 1.5%, only 15 patients per 1,000 would have PE. Anticoagulating patients with a 1.54% probability of PE would mean exposing 65 patients (i.e., 1/0.0154) to the harms of anticoagulation to benefit one patient with a PE. Most physicians would follow this patient closely without giving specific treatment for PE. This same logic can be applied to all screening and diagnostic tests for PE, including D-dimer testing (high sensitivity and low specificity), which is therefore more useful for ruling out PE (when it is negative) than ruling it in (when it is positive).22 D-dimer tests can also be used for calibrating clinical observations to enhance the quantitation of pretest probabilities.23
Measures of treatment effects
One of the most important tasks of clinicians is to advise patients about the current best treatment for their condition. Such advice should be based on the best evidence available. Clinically useful measures of treatment effects reported in clinical trials include the experimental event rate (EER), the control event rate (CER), relative risk reduction (RRR), absolute risk reduction (ARR), the number needed to treat (NNT), and the number needed to harm [see Table 4]. These measures can be effective tools for quantifying the magnitude of treatment benefits and risks, provided that there is a statistically significant difference in the clinical event rate between experimental subjects and control subjects (i.e., between the EER and the CER).
Again, we illustrate the practical application of these terms by a specific example. A 69-year-old hypertensive male smoker has experienced a partial left hemispheric stroke, with good recovery of function. He has a 75% ipsilateral internal carotid artery stenosis. One option would be to give this patient aspirin or clopido-grel and manage his risk factors for cerebrovascular disease; another would be to offer him carotid endarterectomy in addition to medical treatment. The question is, how and on what evidentiary basis does the clinician choose one treatment over another? It is tempting to think of treatments in black-and-white terms, as either working or not working, but the reality is rarely so absolute; often, the choice is between two or more treatments, each of which works after a fashion in certain situations. To apply the available evidence to the decision-making process in the most effective manner, the clinician must interpret it quantitatively, offering accurate, relevant figures instead of gut feelings when the patient asks what his chances are with each therapeutic approach.
Three randomized, controlled trials of carotid endarterectomy for symptomatic carotid artery stenosis24-26 can inform our choice of treatment in this hypothetical patient. Examination of the North American Symptomatic Carotid Endarterectomy Trial (NASCET)24 in the light of the users’ guides discussed earlier [see Table 1] reveals that this study meets the three criteria for a study focusing on therapy. First, patients with symptomatic hemispheric transient ischemic attacks or partial strokes and ipsilater-al carotid stenoses of 70% to 99% were randomly assigned to either an experimental group that underwent carotid endarterec-tomy or a control group that did not. All patients received continuing medical care, with special attention given to risk factors for cerebrovascular disease. Second, the study assessed the effect of carotid endarterectomy on important clinical events— namely, recurrence of stroke or perioperative stroke or death. Third, none of the patients were lost to follow-up. Consequently, the data from the study are likely to be valid guides in determining which treatment is best for this patient.
In the NASCET report, the risk of major or fatal ipsilateral stroke within a 2-year follow-up period was 2.5% in the group that underwent carotid endarterectomy and 13.1% in the control group. The absolute risk reduction, therefore, was 13.1% – 2.5%, or 10.6% (P < 0.001; CI, 5.5% to 15.7%), and the relative risk reduction was 10.6%/13.1%, or 81%. The number needed to treat was 10 (1/0.106); that is, 10 patients (CI, 7 to 18) would have to be treated with carotid endarterectomy (rather than medical treatment alone) to ensure that one major or fatal ipsilateral stroke would be prevented. The NASCET report indicates that this benefit is somewhat lower for patients with less severe stenosis (70% to 79%) and somewhat higher for patients with multiple risk factors for cerebrovascular disease—circumstances that offset one another in the case of the patient under consideration here.
Having determined the NNT, the next question is whether an NNT of 10 for major or fatal stroke over a 2-year period is a small benefit or a large one. By contrast, treatment of elevated diastolic blood pressures that do not exceed 115 mm Hg is associated with an NNT of 167 to prevent one stroke over a 5-year period.25 Thus, for patients who have symptomatic, severe carotid artery stenosis, carotid endarterectomy is highly beneficial.
Given this conclusion, the next question is, do these research results apply to a specific patient, hospital, and surgeon? For example, the NASCET data reflect operative procedures performed by highly competent surgeons in specialized centers. One would have to know the perioperative complication rates for local surgeons to be able to assess a patient’s level of risk if referred to any of those surgeons. If the local surgeons’ periop-erative complication rates for carotid endarterectomy are lower than 7%, the results are comparable to the NASCET results. On the other hand, patients with a stenosis of less than 70% are at substantially less risk for subsequent stroke to begin with. Potential benefit is similar to potential harm for patients with stenoses of 50% to 70%; for patients with stenoses of less than 50%, current evidence indicates that carotid endarterectomy would not yield any net reduction of this risk, even when the procedure is done by a highly skilled surgeon.26,27
Measures of treatment outcome, adjusted for quality of life
Measures of treatment outcome, such as reduction in mortality, are important in deciding whether to start a medication or perform an operation, but they do not answer a question that is important to many patients: How much longer can they expect to live if treatment is started? One way of responding is to frame the answer in terms of life expectancy, the average length of life after starting treatment, which has a simple relation to the annual mortality in patients undergoing treatment.13
Although life expectancy is a useful measure of treatment outcome, it has one shortcoming: it places the same value on years in perfect health as on years in poor health. Arguably, a year with partially treated chronic disease is not equivalent to a year in perfect health. A solution to this problem is to adjust life expectancy for the quality of life that the patient experiences during a year of poor health by multiplying life expectancy by a number, expressed on a scale of 0 to 1, that reflects how the patient feels about the quality of life experienced during an illness. This number is usually called a utility. When life expectancy, expressed in years, is multiplied by a utility, the result is a quality-adjusted life year (QALY). One QALY is equivalent to a year in perfect health.
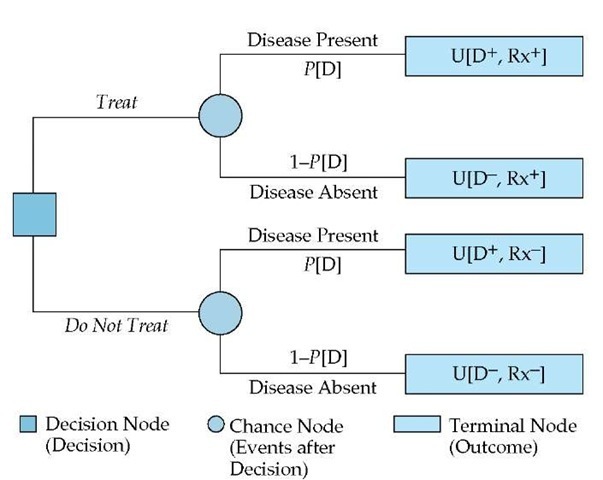
Figure 2 Shown is a decision tree for calculating the treatment threshold probability in a patient who is a possible candidate for carotid endarterectomy. (D—disease; U—utility)
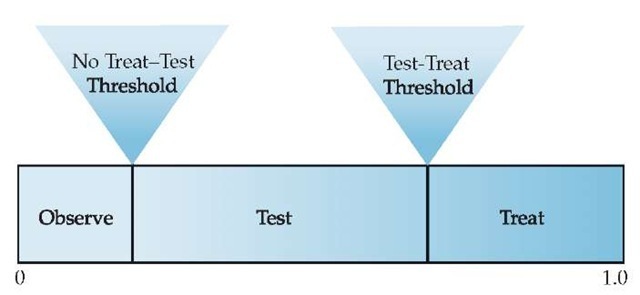
Figure 3 Probability scale showing the ranges of probability corresponding to different actions following the initial history and physical examination.