Gravity - The Solid Earth - page 194

P

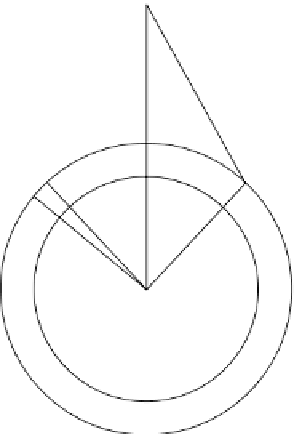
Figure 5.2. A strip of a
thin, spherical shell with
centre O. P is an arbitrary
point at distance r from O.

D

Q

bd q

b

b

t

q

d q

O

The potential of the entire spherical shell can now be evaluated from Eq. (5.6)
by integrating the potential of the strip:

=− G ρ t 2 π b 2

sin θ d θ

V (5.8)

( r 2 + b 2 − 2 br cos θ ) 1 / 2

To evaluate this integral, we need to change it from an integral over θ to an integral

over D . Differentiation of Eq. (5.7)gives

D d D = br sin θ d θ (5.9)

Equation (5.8)isthen written

=− G ρ t 2 π b 2

D max

d D
br

V (5.10)

D min

To evaluate this integral, it is necessary to consider two situations: (i) when P is
outside the spherical shell ( r

> b ) and (ii) when P is inside the spherical shell

( r b ).

(i) When the point P is external to the spherical shell, as in Fig. 5.2, the limits
D min and D max are r-b and r

<

+ b , respectively, and the potential at point P is

=− G ρ t 2 π b 2 D
br

r + b

V

r − b

G ρ t 4 π b 2
r

=− (5.11)

b 2

t , and so, at the point P the
potential of the shell is the same as that due to an equal mass placed at O, the
centre of the shell. The gravitational acceleration a due to the spherical shell can
be calculated from Eq. (5.4) (in spherical polar coordinates) as
a =− ∂ V

The total mass of the spherical shell is 4 π ρ

G ρ t 4 π b 2
r 2 ∂ r =−

(5.12)