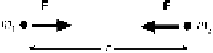Gravity - The Solid Earth - page 193

The gravitational acceleration , a ,ofmass m 2 towards m 1 (with the acceleration
taken to be positive in the outward radial direction) can be written in terms of the
potential V by using Eq. (5.2):

Figure 5.1. Two masses
m 1 and m 2 ,atdistance r
apart, attract each other
with force F = Gm 1 m 2 / r 2 .

Gm 1
r 2
=− ∂
∂ r

a =−

Gm 1
r

−

=− ∂ V
∂ r

(5.3)

If we generalize Eq. (5.3) from one to three dimensions, it is written as

a =− grad V (5.4)

or

a =−∇ V

(See Appendix 1 for discussion of grad or ∇ .)

If, instead of just one mass m 1 ,weimagine a distribution of masses, we can
then define a potential V as

=− G
i

m i
r i

V (5.5)

or

=− G

d m
r

V (5.6)

m

where (in Eq. (5.5)) each mass m i is at position r i and (in Eq. (5.6)) the integral
over m is summing all the infinitesimal masses d m , each at its position r . The
gravitational acceleration due to either of these distributions is then again given
by Eq. (5.4).
We can now use Eq. (5.6)tocalculate the potential of a spherical shell (Fig. 5.2).
Let us calculate the potential at a point P at distance r from the centre O of the
shell. Consider the thin strip of shell, half of which is shown (stippled) in Fig. 5.2.
This circular strip has an area of

(2 π b sin θ )( b d θ )

If we assume the shell to be of thickness t (and very thin) and to be of uniform
density

ρ , the total mass of the strip is

ρ t 2 π b 2 sin θ d θ

Because every point on the strip is the same distance D from point P, Eq. (5.2)
gives the potential at P due to the strip as

G ρ t 2 π b 2 sin θ d θ
D
Applying the cosine formula to triangle OQP gives D in terms of r, b and

−

θ as

D 2 r 2 b 2 = + − 2 br cos θ (5.7)