Schwerefeld und Figur der Erde - Einfuhrung in die Geophysik - page 158

von gleicher Masse sind, ebenso wie alle anderen ungerad-
zahligen Koeffizienten, welche Potenziale von Multipolen
höherer Ordnungen beschreiben: 0 D c 1 D c 3 D c 5 D :::
Damit ist der dritte Term ( ` D 2 ) mit dem Koeffizien-
ten c 2 der niedrigste Term der Entwicklung, der durch den
Äquatorwulst und die Polabplattung die Abweichung des
Sphäroids von einer Kugel beschreibt. Er kann durch die
dynamische Abplattung J 2 der Erde ausgedrückt werden:
c 2 D J 2 D. C A /=. M E a 2 / , wobei C und A die
Hauptträgheitsmomente der Erde bezüglich ihrer polaren
und äquatorialen Radien c und a sind. Allgemein werden die
Koeffizienten in ( 4.53 ) oftmitJ ` statt mit c ` bezeichnet. So-
mit vereinfacht sich ( 4.53 ) fürr > azu:

" #

X

GM E
r

. a = r / 2` J 2` P 2` . cos ™ 0 / U g D 1 : (4.54)

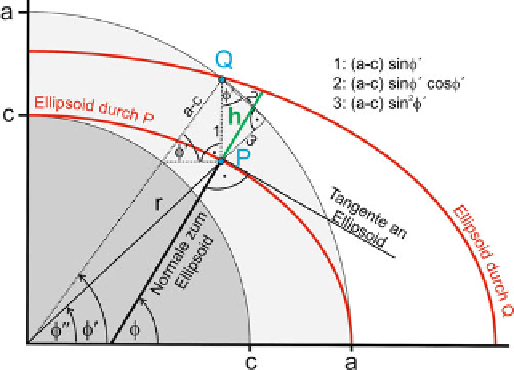
Abb. 4.22 Geografische, reduzierte und geozentrische Breiten ¥ , ¥ 0
und ¥ 00 eines Punktes P im radialen Abstand r vom Mittelpunkt des Re-
ferenzellipsoids mit den großen und kleinen Halbachsen a und c sowie
Höhe h eines Punktes Q über dem Referenzellipsoid

` D 1

Hinzufügen des Zentrifugalpotenzials ( 4.22 ) ergibtdasge-
meinsame Schwerepotenzial der Gravitations- und Zentrifu-
galbeschleunigungen:

gelten die Beziehungen:

" #

X

GM E
r

tan ¥ D . a = c / 2 tan ¥ 0 D 1;003 364 tan ¥ 0 D . a = c / 2 tan ¥ 00
D 1;006 740 tan ¥ 00 ;

. a = r / 2` J 2` P 2` . cos ™ 0 /

U D U g C U z D 1

(4.51) ` D 1

2 r 2
2

sin 2 ™ 0 : (4.55)

mit den GRS80-Werten für a und c (Tab. 7.7 ) . Für kleine
Werte der Abplattung f ( 4.20 ) gelten folgende Näherungen,
deren Gültigkeit man in Abb. 4.22 ersehen kann: Die Koeffizienten J 2 ` in ( 4.55 ) werden mit Hilfe von Da-

ten aus der Satellitengeodäsie bestimmt. Im GRS80 sind
die folgenden Werte festgelegt: J 2 D 108 263 10 8 ;
J 4 D237;091 222 10 8 ;J 6 D 0;608 347 10 8 ;J 8 D
0;001 427 10 8 . Abbrechen der Entwicklung nach dem
quadratischen Term ( ` D 1 ) und Einsetzen des Beschleu-
nigungsquotienten aus äquatorialer Zentrifugal- und Gravi-
tationsbeschleunigung m D a z = a g D 2 r 3 = GM E ( 4.21 )
sowie des legendreschen Polynoms P 2 D

¥ 00 D ¥ fsin

(in Grad) I
r a .1 fsin 2 ¥/ D 6378;137 21;385 sin 2 ¥

.2¥/ D ¥ 0;19 sin .2¥/

(in km) :
(4.52)

Damit vereinfacht sich die Entwicklung ( 4.48 ) des Gravitati-
onspotenzials U g nach Kugelflächenfunktionen für r > azu
einer Entwicklung ( 3.115 ) nach legendreschen Polynomen:

1

2 .3 cos 2 ™ 0 1/

X

GM E
r

U g .™ 00 ;œ/ D . a = r / ` c ` P ` . cos ™ 0 /

` D 0

2 3

c 0 P 0 . cos ™ 0 /
„ ƒ‚ …
1

C. a = r / c 1 P 1 . cos ™ 0 /
„ ƒ‚ …
cos ™ 0

C. a = r / 2 c 2 P 2 . c os ™ 0 /C
„ ƒ‚ …
.3 cos 2™ 0 C 1/=4

4 5 :

GM E
r

D (4.53)

/ 3 c 3 ™ 0 /

„ ƒ‚ …

/ 4 c 4 ™ 0 /

„ ƒ‚ …

C. a = r P 3 . cos C. a = r P 4 . cos C :::

.5 cos 3™ 0 C 3 cos ™ 0 /=8 .35 cos 4™ 0 C 20 cos 2™ 0 C 9/=64

Die Koeffizienten in ( 4.53 ) beschreiben hierbei die Gewich-
tung der einzelnen Terme. Der erste Summand ( ` D 0 )
dieser Entwicklung beschreibt das Potenzial GM E =

aus Tab. 3.13 ergibt:

reines
Monopols - daher ist c 0 D 1 . Der zweite Term ( ` D 1 )
beschreibt einen nach Norden weisenden (

GM E
r

U D

) zentralen
Dipol. Da der Koordinatenursprung im Massezentrum liegt,
muss bei der vorausgesetzten homogenen Massenverteilung
der Koeffizient verschwinden, da Nord- und Südhalbkugel

™ D 0

3
2 GM E sin 2 ™ 0

1 a

r 2 J 2

2 r 3
2

1
2

cos 2 ™ 0 C :

(4.56)