Image Processing Reference
In-Depth Information
The activation function may be a simple threshold function, a sigmoid hyperbolic tangent,
(1)
Back propagation is a common training technique for an NN. This training process requires
the NN to perform a particular function by adjusting the values of the connections (weights)
dressed: selection of data samples for network training, selection of an appropriate and ei-
Moreover, an NN has many advantages, such as the good learning ability, less memory de-
mand, suitable generalization, fast real-time operating, simple and convenient utilization, ad-
eptness at analyzing complex paterns, and so on. On the other hand, an NN has some disad-
vantages, including its requirement for high-quality data, the need for careful
a priori
selection
5 Overview of the classification and regression tree
C&R trees are the most common and popular nonparametric DT learning technique. In this
chapter, I only use a regression tree for numeric data values. C&R builds a binary tree by split-
ting the records at each node according to a function of a single input variable. The measure
used to evaluate a potential spliter is diversity. This method uses recursive partitioning to
impurity used at each node can be defined in the tree by two measures: entropy, as in Equa-
tion
(2)
, and Gini, which has been chosen for this chapter. The equation for entropy follows.
(2)
The Gini index, on the other hand, generalizes the variance impurity, which is the variance
as the expected error rate if the class label is randomly chosen from the class distribution at
the node. In such a case, this impurity measure would have been slightly stronger at equal
probabilities (for two classes) than the entropy measure. The Gini index, which is defined by
the following equation, holds some advantages for an optimization of the impurity metric at

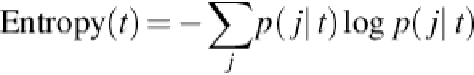
Search WWH ::

Custom Search