Cryptography Reference
In-Depth Information
However, instead of selecting the subkey with the most hits, we instead eliminate any key that ever shows an
impossible difference.Repeating this enough times, we will eventually be left with a single candidate subkey.
Repeat this a sufficient number of times for different subkeys, and we will eventually be left with a reasonable
number of keys to check through brute-force. Performing a 25-round attack can recover the full key in about 2
27
steps. However, when we hit 26 rounds, this becomes 2
49
steps and gets worse from there.
The above key recovery attack, unfortunately, only seems to work for up to about 26 rounds of the full
32-round Skipjack. With 31 rounds, Biham et al. [4] instead found that they would have to check every single
key. Luckily, checking every single key does not require performing the complete encryption or decryption: It
can be limited to a handful of computations of the
G
-function. Since a full encryption works by using several
G
-function computations, as long as we keep the number of
G
computations down below the amount required
for a full encryption, we are still doing less work than would be required on a normal exhaustive attack. The
authors predict about 2
78
steps, with 2
64
bits of memory (2,048 petabytes). This is still faster than an exhaustive
attack, which would require 2
80
steps.
One of the most important contributions of the concept of impossible differentials is that the normal method
of“proving”ciphersecureagainstdifferential cryptanalysis —thatbycreating averylowupperboundonprob-
abilities of differentials in the components — is flawed. If there are a sufficient number of zero or low-probab-
ility differentials, then the impossible differential attack can be carried out.
Furthermore, this same attack can be applied with conditional characteristics and differentials, as well as lin-
ear cryptanalysis.
7.14 Boomerang Attack
So far, we have been focusing almost entirely on top-down approaches to cryptanalysis: Our attacks work by
taking information about the plaintext, and deriving some feature of the ciphertext that we will test. How often
the test succeeds gives us a likelihood that a key is correct.
Theaboveattackwithimpossibledifferentials,aswellasthepreviouslydiscussedmeet-in-the-middle attack,
shows us that this view may be missing out on some advantages to working both ends at once. Linear cryptana-
lysis even uses some of this symmetry to help derive more key bits.
The
boomerang attack
is another differential meet-in-the-middle attack [20].
The basic premise uses four pairs of plaintexts and their associated ciphertexts:
Using the premises of Reference [20], let's break the encryption operation (
E
) into two subparts:
E
0
(the first
half of the encryption) and
E
1
(the second half of the encryption). For example:
I'll denote the inverse operations of
E
0
and
E
1
, as in, the decryption operations, as
E
0
-1
and
E
1
-1
, respectively.
From the above, we would also have
Here, we will have to develop two characteristics, one for the first half of the encryption,
E
0
, and one for the
second half's decryption,
E
1
-1
:
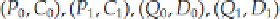

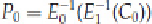
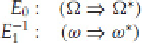
Search WWH ::

Custom Search