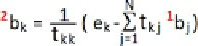Graphics Reference
In-Depth Information
d. h.
[T]
ist diagonaldominant. Diese Eigenschaft ist Voraussetzung zur iterativen
Lösung des Gleichungssystems.
Die Gauß-Seidel-Iteration ist eine Möglichkeit, das LGS zu lösen. Eine erste
Näherung erhält man, wenn man obiges Schema nach den Diagonalgliedern auflöst
(t
;
b
;
e sind die Elemente der Matrizen
[T]
,
{B}
,
{E}
):
t
11
b
1
D
e
1
t
12
b
2
t
13
b
3
t
14
b
4
:::
t
22
b
2
D
e
2
t
21
b
1
t
23
b
3
t
24
b
4
:::
t
33
b
3
D
e
3
t
31
b
1
t
32
b
2
t
34
b
4
:::
t
44
b
4
D
e
4
t
41
b
1
t
42
b
2
t
43
b
3
:::
Bei dominanten Hauptdiagonalelementen t
kk
lassen sich die rechts stehenden Glie-
der als relativ kleine Korrekturen auffassen. Aus der ersten Gleichung erhält man
das Element b
1
als neue Näherung, das bereits in der zweiten Gleichung verwendet
wird. In der zweiten Gleichung ergibt sich ein verbessertes b
2
, das schon mit dem
verbesserten b
1
berechnet wurde usw. Dieser Ablauf wird so lange wiederholt, bis
alle Elemente von
{B}
innerhalb einer gegebenen Toleranz stabil sind. Ein Iterati-
onsschritt lautet also:
Hierin ist vorausgesetzt, dass die Diagonalelemente t
kk
aus der
[T]
-Matrix entfernt
sind und separat als
1=
t
kk
vorgehalten werden. Die Summenbildung erfolgt als Ska-
larprodukt einer Matrixzeile
(t
k
;::
)
mit dem Spaltenvektor
{B}
; siehe Abschn.
11.2
.
Da die Ordnung N der Systemmatrix
[T]
groß ist, muss folglich das Skalarpro-
dukt sehr effektiv programmiert werden. Leider macht es wenig Sinn, diese N
Skalarprodukte zu parallelisieren, da ja stets auf die bereits zuvor berechneten b
k
zurückgegriffen wird. Die ganze Vorgehensweise wird als „Full-Matrix“-Methode
bezeichnet.
Für die praktische Berechnung ist die Bildung von
[T]
ein ganz unnötiger Schritt.
Die beiden folgenden Verfahren verwenden die Ausgangsdaten unmittelbar.
Neben der „Full-Matrix“-Methode gibt es zwei weitere, ebenfalls iterative Lösungs-
strategien, deren Bezeichnungen sich aus ihrer matriziellen Organisation ableiten:
Gathering
und
Shooting
.