Biomedical Engineering Reference
In-Depth Information
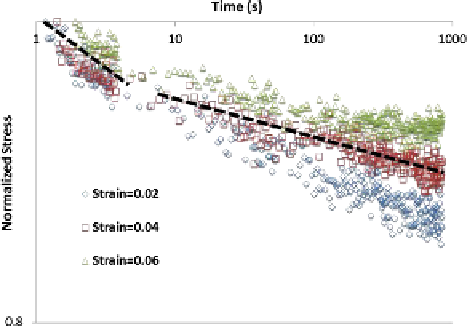
Fig. 25.3
Bi-linear stress
relaxation response of native
ACL
25.2.2 A 3D Viscoelastic Constitutive Model
The simplest viscoelastic model that can capture solid-like behavior is the standard
linear solid model the 1D analog of which has two linear springs and a linear dash-
pot. The configuration of this model can be represented with springs of stiffness
k
1
and
k
2
and a dashpot with viscosity
η
1
,asinFig.
25.1
. The model describes the lin-
ear viscoelastic behavior of solids well. In the extension to 3D each spring becomes
a 3D linear elastic stress-strain relationship (i.e. Hooke's law) and the dashpot be-
comes a 3D linear viscous element. Since the ACL and its grafts have a nonlinear
viscoelastic behavior, we substitute a nonlinear MacKintosh semi-flexible network
of Fig.
25.3
for one linear stress-strain relationship. We have examined various pos-
sibilities for the remaining elements in the three-element model and found the com-
bination of a second nonlinear elastic network and a linear dashpot to capture liga-
ment and tendon viscoelasticity reasonably well, but not fully accurately (Ma et al.,
2010
). Our previous stress relaxation experiments have demonstrated that ACLs
and tissue engineered grafts have the distinct bi-linear relaxation behavior shown in
Fig.
25.4
that may be captured by two linear elastic networks and two linear viscous
elements. Therefore, the proposed model consists of five elements as illustrated in
1D in Fig.
25.4
, a nonlinear elastic network, two linear elastic networks and two
linear viscous elements.
In this model
F
e
B
and
F
e
C
are the elastic parts of the deformation gradient tensors
and
F
B
and
F
C
are the viscous parts. From compatibility, the total deformation
F
is
F
F
e
B
F
B
=
F
e
C
F
C
. The left Cauchy-Green tensor
B
is
B
FF
T
. From equilibrium
=
=
=
T
A
+
T
B
+
of the system, the total Cauchy stress is given as
T
T
C
, where
T
A
is
the Cauchy stress in the nonlinear spring network
A
, given by Fig.
25.4
, and
T
B
and
T
C
are the Cauchy stresses in the linear spring networks
B
and
C
. The Cauchy
stress tensors in the linear networks can be represented as follows:
nkΘ
B,C
B
e
B,C
−
T
B,C
=
p
I
.
(25.7)