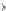Image Processing Reference
In-Depth Information
ϕ
1
ϕ
2
2
2
1.5
1.5
1
1
0.5
0.5
s
s
s
0
0
-2
-1
1
2
-2
-1
1
2
-0.5
-0.5
-1
-1
∂ϕ
1
∂ϕ
2
3
3
2
2
1
1
s
s
0
0
-2
-1
1
2
-2
-1
1
2
-1
-1
-2
-2
Abbildung 6.8.
Beispiele für das Subdifferential konvexer Funktionen. Oben jeweils der Graph, unten die asso-
ziierten Subdifferentiale. Die eingezeichneten affinen Stützfunktionen korrespondieren jeweils mit den mar-
kierten Punkten im Subdifferential. Die Funktion
ϕ
1
ist bis auf den Nullpunkt differenzierbar, dort entspricht
der Subgradient einem kompakten Intervall; der Subgradient des Indikatorfunktionals
ϕ
2
ist an den Rand-
−
[
−
]
punkten
1 und 1 jeweils die nicht-positive bzw. nicht-negative reelle Achse. Außerhalb von
1, 1
ist er
leer.
Erstere ist überall in
R
\{
0
}
differenzierbar. Im Nullpunkt gibt es einen Knick, man sieht
1
2
t
2
leicht ein, dass
st
≤
+
t
für alle
t
≥
0 genau dann, wenn
s
≤
1. Analog gilt
st
≤
10
t
2
3
1
1
1
−
≤
≥−
(
)=[
−
]
4
t
für alle
t
0 genau dann, wenn
s
4
. Daher ist
∂ϕ
1
0
4
,1
.
konstant, also differenzierbar mit Ableitung 0. Im
Punkt 1 stellen wir sofort fest, dass
s
Die Funktion
ϕ
2
ist in
]
−
1, 1
[
(
−
)
≤
∈
[
−
]
t
1
0 für alle
t
1, 1
genau dann,
wenn
s
≥
0. Dies zeigt
∂ϕ
2
(
1
)=[
0,
∞
[
. Mit einem analogen Argument sehen wir
∂ϕ
2
(
−
1
)=]
−
∞
,0
]
, in allen anderen Punkten ist der Subgradient leer. Zusammenge-
fasst gilt also
⎧
⎨
⎧
⎨
]
−
∞
,0
]
falls
t
=
−
1,
6
1
4
{
10
t
−
}
falls
t
<
0,
{
0
}
falls
t
∈
]
−
1, 1
[
,
1
∂ϕ
1
(
t
)=
∂ϕ
2
(
t
)=
[
−
4
,1
]
falls
t
=
0,
⎩
⎩
[
∞[
=
0,
falls
t
1,
{
t
+
1
}
falls
t
>
0,
∅
sonst,
siehe auch Abbildung 6.8.
Als Vorbemerkung zu den kommenden Beweisen sei festgestellt, dass sich ein Ele-
ment des Subgradienten geometrisch interpretieren lässt. Jedes
w
∈ ∂
(
)
F
u
entspricht
nämlich via
)
{
(
−
=
−
(
)
}
v
,
t
w
,
v
t
w
,
u
F
u
{
u
,
F
)
}
einer abgeschlossenen Hyperebene in
X
trennt. Sie ist
„nicht-vertikal“ in dem Sinn, dass ihre Projektion auf
X
ganz
X
ergibt. Zum Vergleich:
×
R
, die epi
F
von
(
u