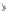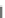Image Processing Reference
In-Depth Information
ϕ
1
ϕ
2
2
2
1.5
1.5
1
1
0.5
0.5
s
s
-2
-1
0
1
2
-2
-1
0
1
2
(a)
u
0
u
1
u
2
u
3
1
1
1
1
0
0
0
0
1
1
1
1
-1
-1
-1
-1
u
u
4
u
5
1
1
1
···
0
0
0
1
1
1
-1
-1
-1
(b)
Abbildung 6.5.
Veranschaulichung der in Beispiel 6.18 benutzten Funktionen. (a) Die punktweisen „Energie-
funktionen“
u
n
ϕ
1
und
ϕ
2
. (b) Die ersten Folgenglieder von
(
)
sowie der schwache Grenzwert
u
.
Beispiel 6.18
(Beispiel/Gegenbeispiel zur schwachen Unterhalbstetigkeit)
Es sei
X
L
2
1
2
x
2
1
4
2
2
, zu sehen in Abbil-
=
([
])
(
)=
(
)=
(
−
)
(
+
)
0, 1
,
ϕ
1
x
und
ϕ
2
x
x
1
x
1
dung 6.5(a). Betrachte die Funktionale
1
1
ϕ
1
u
)
d
t
,
ϕ
2
u
)
d
t
.
(
)=
(
(
)=
(
F
1
u
t
F
2
u
t
0
0
Nun ist
F
1
=
ϕ
1
◦·
2
als Folge von Korollar 6.15 schwach unterhalbstetig auf
X
. Für
F
2
ist dies jedoch nicht wahr: Die Folge
u
n
(
)
gegeben durch
1
falls 2
k
≤
t
<
2
k
+
1 für ein
k
∈
Z
u
n
2
n
t
(
)=
(
)
(
)=
t
v
,
v
t
−
1
sonst
ist eine Menge paarweiser orthonormaler Vektoren und konvergiert daher nach der
Standardaussagen der Hilbert-Raum-Theorie (siehe Unterabschnitt 2.1.3) schwach ge-
gen
u
=
0 (siehe auch Abbildung 6.5(b)), jedoch gilt:
1
4
,
u
n
∀
n
∈
N
:
F
2
(
)=
0,
F
2
(
u
)=
u
n
daher
F
2
.
Obwohl die Funktionale
F
1
und
F
2
eine ähnliche Struktur haben, unterscheiden sie
sich in der schwachen Unterhalbstetigkeit. In der Tat ist die Tatsache, dass
(
u
)
>
lim inf
n→
∞
F
2
(
)
ϕ
1
konvex
ist und
ϕ
2
nicht, dafür verantwortlich. Eine Erklärung hierfür liefert die Theorie der
Konvexen Analysis
, das Thema das nächsten Abschnitts.
Wir werden im Laufe des Kapitels zu der Thematik der schwachen Unterhalbstetig-
keit von Funktionalen zurückkehren, schließen doch zunächst die Diskussion mit einer
Bemerkung ab.