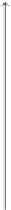Image Processing Reference
In-Depth Information
φ
j
,
k
2
−
j
/2
φ
1
1
2
j
k
2
j
(
k
+
1
)
ψ
ψ
j
,
k
Abbildung 4.13.
Skalierungsfunktion und Wavelets zur stückweise konstanten Multiskalenanalyse.
Beweis.
Zuerst rechnet man nach, dass für alle
k
∈
Z
gilt
(
ψ
)=
,
φ
k
,0
0
(
ψ
,
ψ
k
,0
)=
δ
0,
k
ψ ⊥
ψ ∈
(Aufgabe 4.16). Die erste Gleichung zeigt
V
0
und damit
W
0
. Die zweite Glei-
chung zeigt die Orthonormalität der Translate von
ψ
.
{ψ
k
,0
k
∈
}
Nun zeigen wir, dass das System
Z
vollständig in
W
0
ist. Äquivalent da-
ψ
k
,0
k
zu ist, dass das System
{
φ
k
,0
,
∈
Z
}
vollständig in
V
−
1
ist, da
V
=
V
0
⊕
W
0
.
ψ
k
,0
k
−
1
{φ
k
,0
,
∈
}
Wir zeigen letzteres indem wir zeigen, dass
dargestellt
werden kann. Hierzu rechnen wir mit Hilfe der Skalierungsgleichung (4.4) und der De-
finition von
φ
−
1,0
durch
Z
ψ
nach
2
2
k
∈
Z
|
(
φ
−
1,0
,
ψ
k
,0
)
|
+
|
(
φ
−
1,0
,
φ
k
,0
)
|
=
k
∈
Z
l
∈
Z
h
l
(
φ
−
1,0
,
φ
−
1,
l
+
2
k
)
2
2
l
∈
Z
(
−
1)
l
h
1
−l
+
(
φ
−
1,0
,
)
φ
−
1,
l
+
2
k
=
δ
0,
l
+2
k
=
δ
0,
l
+2
k
=
k∈
Z
h
2
h
1+2
k
=
k∈
Z
h
k
.
−
2
k
+
∑
k∈
Z
h
k
=
φ
−
1,0
=
In Aufgabe 4.16 zeigen Sie insbesondere
1 und wegen
1 folgt, dass
ψ
k
,0
k
das System
−
1
vollständig ist. Die Behauptungen 1. und 2. folgen
nun durch einfache Argumente (vergleiche Aufgabe 4.14). Für 3. verweisen wir auf [9
5].
{
φ
k
,0
,
∈
}
in
V
Z
{ψ
j
,
k
j
,
k
∈
}
Im Kontext von Satz 4.67 sagen wir auch: Die Menge
Z
ist eine ortho-
normale Wavelet-Basis von
L
2
(
)
R
.