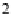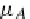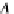Database Reference
In-Depth Information
We recall that a monad
(T,η,μ)
(from Proposition
9
in Sect.
3.2.1
, the endofunctor
T
:
DB
→
DB
is a monad), given by commutative diagrams
defines an adjunction
(F
T
,G
T
,η
T
,
T
)
:
−→
CT
alg
such that
G
T
◦
F
T
DB
=
DB
,
η
T
η
,
T
η
OP
G
T
T
F
T
. The functors
F
T
T
→
CT
alg
(into the Eilenberg-Moore category of
monadic
T-algebras, associated to the
monad
(T, η,μ)
) and forgetful functor
G
T
:
DB
−→
=
=
and
μ
=
:
DB
:
CT
alg
→
DB
are defined as follows:
for any object (database)
A
,
F
T
(A)
T
2
A
TA)
,
F
T
(f )
=
(T A,μ
A
:
→
=
Tf
while
G
T
(A,g
:
TA
→
A)
=
A
and
G
T
(f )
=
f
.
Let us consider the following properties for monadic algebras/coalgebras in
DB
(introduced by Definition
24
and
25
in Sect.
3.2.1
):
Proposition 57
The following properties for the monad (T, η,μ)
and the
comonad (T, η
C
,μ
C
) hold
:
•
The Eilenberg-Moore categories CT
alg
and CT
coalg
of the monad T
:
DB
−→
DB
(
from Proposition
9
)
are isomorphic
(
CT
coalg
=
CT
OP
),
complete and co-
alg
0
, id
0
0
) is an initial T-algebra in CT
alg
and
complete
.
The object (
⊥
:⊥
−→ ⊥
0
⊥
a terminal T-coalgebra in CT
coalg
.
•
For each object A in
DB
category there exist the unique monadic T-algebra
(A,η
A
:
TA
−→
A) and the unique comonadic T-coalgebra (A,η
A
:
A
−→
TA)
with η
A
=
η
OP
A
(
i
.
e
.,
η
A
=
is
−
A
≈
η
A
=
is
A
≈
id
A
).
T
2
A
•
The free monadic T-algebra (T A,μ
A
:
−→
TA) is dual
(
and equal
)
to
the cofree monadic T-coalgebra (T A,μ
A
:
T
2
A) with μ
A
=
μ
OP
A
TA
−→
(
i
.
e
.,
μ
A
=
μ
A
=
id
TA
).
:
CT
alg
−→
Proof
Let us define the functor
F
CT
coalg
such that for any T-algebra
A)
we obtain the dual T-coalgebra
F
0
(A,h)
(A,h
OP
(A,h
−→
TA)
, where the component
F
1
for the arrows is an identity function; and the functor
F
:
TA
−→
=
:
A
:
CT
coalg
−→
CT
alg
such that for any T-coalgebra
(A,k
:
A
−→
TA)
we obtain
the dual T-algebra
G
0
(A,k)
(A,k
OP
A)
, where the component
G
1
=
:
TA
−→
for
=
=
the arrows is an identity function. Hence,
FG
I
T
alg
. The cate-
gories
CT
alg
and
CT
coalg
are complete and cocomplete as
DB
category (
CT
coalg
=
CT
OP
I
T
coalg
and
GF
alg
). The rest is easy to verify (by Proposition
9
and Corollary
11
in Sect.
3.2.1
):
each monadic T-algebra/coalgebra is an isomorphism. The free monadic T-algebra
and the cofree monadic T-coalgebra are equal because
TA
T
2
A
, thus,
μ
A
,μ
A
are
=
identity arrows (from duality property of
DB
).