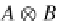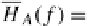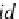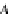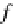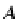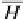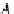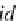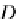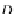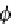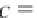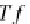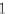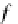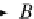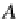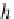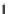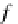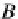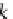Database Reference
In-Depth Information
For
ea
ch arrow g
OP
A in
D
B
OP
,
we define the natural transformation
•
:
D
→
H(g
OP
)
φ
=
=
g
⊗
id
{
_
}
:
H(A)
→
H(D)
.
In fact, this corollary can be represented by the following commutative diagram
in
DB
:
8.3
Database Mappings and (Co)monads: (Co)induction
The notion of a monad is one of the most general mathematical notions for
every
algebraic theory, that is, every set of operations satisfying equational laws can be
seen as a monad (which is also a
monoid
in a category of endofunctors of a given
category: the “operation”
μ
being the associative multiplication of this monoid and
η
its unit). In Sect.
5.1.1
, we considered in details the syntax monads
(
T
P
,η,μ)
in the
Set
category for the relational algebras and, for the particular
Σ
R
(Codd's
SPRJU relational algebra), the relationship with the power-view monad
T
of the
DB
category, which will be here analyzed in more details.
We used monads to provide the
denotational semantics to database mappings
,
as it was explained in Sect.
5.1.1
: in order to interpret database mappings (i.e., mor-
phisms) in the category
DB
, we distinguish the object
A
(a database instance of type
(or schema)
A
) from the object
TA
of observations (i.e., the computations of type
A
without side-effects), and take as a denotation of (view) mappings the elements
of
TA
(which are the views of (type)
A
). In particular, we identify the
A
with the
object of values (of type
), and hence we obtain the object of observations by ap-
plying the unary type-constructor
T
(power-view operator introduced in Sect.
3.2.1
)
to
A
.
It is well known that each endofunctor defines the algebras and coalgebras (the
left and right commutative diagrams bellow), based on Definition
24
in Sect.
3.2.1
:
A