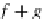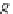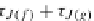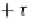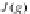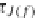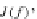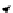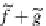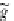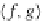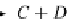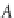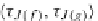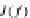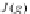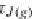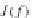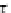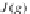Database Reference
In-Depth Information
is
−
1
C
1.1. For
f
+
g
:
A
+
B
→
C
+
D
, from Theorem
2
,
T(f
+
g)
=
D
◦
(f
+
g)
◦
+
(is
−
C
+
is
−
D
)
(is
−
C
◦
(is
−
D
◦
is
A
+
B
=
◦
(f
+
g)
◦
(is
A
+
is
B
)
=
f
◦
is
A
)
+
g
◦
is
B
)
=
Tf
+
Tg
.
is
−
1
A
1.2. For
[
f,g
]:
A
+
B
→
C
, from Theorem
2
,
T(
[
f,g
]
)
=
is
C
◦[
f,g
]◦
B
=
+
(is
−
A
+
is
−
B
)
is
−
A
, is
C
◦
is
−
B
]=[
is
C
◦[
f,g
]◦
=[
is
C
◦
f
◦
g
◦
Tf,Tg
]
.
The other two cases can be proved analogously.
Claim 2. (Duality) It holds from the fact that
f
OP
=
f
. Let us show that Theorem
3
is applicable. For example, consider
[
f,g
]:
A
+
B
→
C
:
is
−
C
◦
Tf
◦
is
B
OP
OP
(
from Th
.
2
)
is
A
, is
−
C
◦
Tg
◦
[
f,g
]
=
=
is
−
C
◦
is
A
OP
,
is
−
C
◦
is
B
OP
Tf
◦
Tg
◦
=
is
−
A
◦
is
C
is
C
, is
−
B
◦
(Tf )
OP
(T g)
OP
◦
◦
f
OP
,g
OP
.
(
from Th
.
3
)
=
Claim 3. The extended symmetry
τ
−
1
•
τ
=
ψ
can be shown by the following four
commutative diagrams;
based on the results in point 1 and the facts of Theorem
4
, i.e.,
τ
J(f)
=
τ
OP
J(f)
=
f
.
For example, in the second case we obtain
τ
−
1
J(g)
◦
=
τ
−
1
J(g)
◦
J(f)
,τ
−
1
J(f)
,τ
−
1
(τ
J(f)
+
(τ
J(f)
τ
J(g)
)
τ
J(g)
)
(
by rule 3 for composition of complex arrows
)
=
τ
−
1
τ
J(g)
=[
τ
J(f)
,τ
−
1
J(f)
◦
J(g)
◦
f,g
]
.
Let us show some examples for the extended symmetry functor
T
e
of Theorem
4
,
applied to complex morphisms and (co)products: