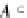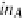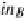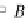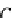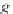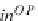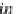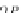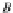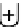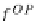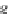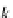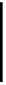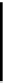Database Reference
In-Depth Information
1
1
1
=
f
(from Definition
20
) and hence this triangle is commutative. Analogously, we
show that
g
Thus,
[
f,g
]◦
in
A
=[
f,g
]◦
id
A
,
⊥
=
f
◦
id
A
,g
◦⊥
=
f,
⊥
=
f
=[
]◦
in
B
.
Let us suppose that there is another arrow
k
=[
f,g
k
1
,k
2
]:
A
+
B
→
C
such that
the diagram above commutes, that is,
k
◦
f
and
k
◦
in
A
=
in
B
=
g
. However,
k
◦
k
1
and
k
◦
1
1
,k
2
=
in
A
=
k
1
,
⊥
=
in
B
=⊥
k
2
, so that
k
1
=
f
and
k
2
=
g
,
that is,
k
=
k
=[
f,g
]
is a unique arrow that satisfies this commutativity.
OP
f
OP
,g
OP
The product diagram is its dual with
k
=[
f,g
]
=
(from Corol-
lary
12
):
Let us show that the complex morphisms with coproducts satisfy the powerview
functor
T
, the duality and the symmetry property in
DB
:
Corollary 12
The complex morphisms satisfy the following
DB
properties
:
1. (
Power-view functorial properties
)
T(f
+
=
+
[
]
=[
]
g)
Tf
Tg
,
T(
f,g
)
Tf,Tg
,
T(
f,g
)
=
Tf,Tg
and T(
f,g
)
=
Tf,Tg
.
g)
OP
f
OP
g
OP
,
OP
f
OP
,g
OP
2. (
The duality properties
)
(f
+
=
+
[
f,g
]
=
,
OP
f
OP
,g
OP
OP
f
OP
,g
OP
f,g
=[
]
and
f,g
=
.
3. (
The symmetry property of Theorem
4
with τ
−
1
•
τ
=
ψ
)
τ
J(f
g)
=
τ
−
1
J(f
g)
=
τ
−
1
τ
−
1
+
τ
J(f)
+
τ
J(g)
,
+
J(f)
+
J(g)
,
τ
J
[
]
=
τ
−
1
J
[
]
=
τ
−
1
J(g)
,
J(f)
,τ
−
1
f,g
τ
J(f)
+
τ
J(g)
,
f,g
τ
J
f,g
=
τ
J(f)
,τ
J(g)
,
τ
−
1
J
f,g
=
τ
−
1
J(f)
+
τ
−
1
J(g)
,
τ
J
=
τ
−
1
J
=
τ
−
1
τ
−
1
f,g
τ
J(f)
∪
τ
J(g)
,
f,g
J(f)
∪
J(g)
.
Proof
Claim 1. (Power-view properties)