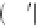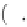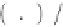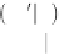Geoscience Reference
In-Depth Information
The acceptance probability depends only on the proposal,
likelihood, and prior functions at the current and
candidate models, all of which can be easily computed.
Assuming that the proposal distribution is symmetric,
q
m
This choice of
s
n
yields an optimal acceptance in the case
of a Gaussian target distribution and a Gaussian proposal
distribution. The candidate model vector,
m
, is accepted
with the acceptance probability:
m
=
q
m
m
(e.g., a Gaussian distribution centered
m
i
−
1
;
m
=min 1,
π
m d
π
m
i
−
1
d
at
the current point),
the acceptance probability
α
4 62
reduces to
m
;
m
=min 1,
P
m d
P
m d
If the candidate model vector is accepted, we consider
that
m
i
=
m
; otherwise, we choose
m
i
=
m
i
−
1
.
The AMA was written in a MATLAB routine that is
coupled with a forward model in COMSOL Multiphysics
3.5 using the finite-element approach described at the
beginning of this section. This algorithm is applied in
the next section to the synthetic seismogram and electro-
gramdata to invert thematerial properties, assuming that
the position of the geological units is known.
α
4 60
This algorithm is known as the original Metropolis
algorithm (Metropolis et al
.
, 1953).
To improve the performance of the standard Metropo-
lis
-
Hastings algorithm, Haario et al. (2001) introduced an
algorithm called the adaptive Metropolis algorithm
(AMA) to find the optimal proposal distribution. This
algorithm is based on the traditional Metropolis algo-
rithm with a symmetric Gaussian proposal distribution
centered at the current model
m
i
andwith the covariance
C
4.3.2 Application
To check the usefulness of the joint inversion of seismic
and seismoelectric data, we test this approach using a
numerical case study. We consider two flat layers plus
a rectangular reservoir embedded in the second layer
(Figure 4.10). The geophones and the electrodes are
located at the top surface of the system to simulate an
onshore acquisition. The takeout for the electrodes and
the geophones has a 10 m separation. The source wavelet
is a first-order derivative of a Gaussian, as defined in
Equation (4.46), with a dominant frequency,
f
0
=30Hz,
and a time delay factor,
t
0
= 0.1 s (see Eq. (4.46)). The
seismic source is located at a depth of 20m (Figure 4.10).
The true values of the material properties used for the sim-
ulation are reported in Table 4.3. With these values, the
velocity of the fast P-wave is 1972m s
−
1
in the first layer
(labeled L1), 2188m s
−
1
in the second layer (labeled L2),
and 3118m s
−
1
in the reservoir (labeled R). The receiver
is located at an offset of
x
= 150m from the source; the time
required for the P-wave to reach this receiver is therefore
0.076 s, in agreement with the numerical simulations
(see succeeding text). The finite-element modeling, based
on COMSOL Multiphysics 3.5, is used to simulate both
seismograms and electrograms at the ground surface.
In Figure 4.11d, the electrograms show the two types
of seismoelectric signals described in the introduction.
The first type of signal corresponds to the coseismic
electrical signal associated with the propagation of the
P-wave. The coseismic electric field related to the direct
field wave from the source to the receiver is labeled
i
that changes during the sampling in such a way that
the sampling efficiency increases over time (Haario
et al., 2001, 2004). The AMA, though not Markovian,
simulates correctly the posterior probability distributions
of the model parameters. An important advantage of the
AMA is that it starts by using the cumulating information
right at the beginning of the simulation. The rapid start of
the adaptation ensures that the search becomes more
effective at an early stage of the simulation, which
diminishes
the number of
iterations
to reach the
convergence of the chain.
The AMA is described as follows. Let us assume that
we have sampled the states (
m
0
,
…
,
m
i
−
1
) where
m
0
corresponds to the model vector of the initial state. Then
a candidate point,
m
, is sampled from the Gaussian
proposal distribution,
q
, with a mean point at the present
point,
m
i
−
1
, and a covariance of
C
0
,
≤
if
i
n
0
,
i
=
C
4 61
i
+
s
n
s
n
K
ε
I
n
, f
i
>
n
0
,
I
n
denotes the
n
-dimensional identity matrix,
K
i
=
Cov(
m
0
,
where
,
m
i
−
1
) is the regularization factor (a small
positive number that prevents the covariance matrix
from becoming singular),
C
0
is the initial covariance
matrix that is strictly positive (note that the AMA is not
too sensitive to the actual values of
C
0
), and
s
n
=24
2
n
is a parameter that depends only on the
dimension of the vector
…
m
ℜ
n
(Haario et al., 2001).