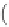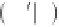Geoscience Reference
In-Depth Information
As usually accepted, the likelihood function used to
assess for the quality of model
m
is Gaussian distributed:
one. Normalizing is not required to perform the inversion
except if we want to compute explicitly the probability
for a given parameter to be in a given interval. In
addition, the normalization can be done at the end of
the computation of the probability density function
(restricting to the numerator), just by normalizing it
(dividing it by its integral) (Grandis et al., 1999).
The Markov chain Monte Carlo (MCMC) family of
algorithms is well suited for Bayesian inference problems
(Malinverno, 2002). MCMC algorithms consist of ran-
dom walks where different states (i.e., different values
of a model vector) are tested and where the choice of
the next state depends only on the value of the current
state. After an initial period in which the random walker
moves toward the highest a posteriori probability
regions, the chain returns a number of model vectors
sampling the posterior probability density
P
d m
=
1
1
2
g
m
d
T
C
−
1
d
1 2
exp
−
−
g
m
−
d
N
det
2
π
C
d
4 55
T
,
d
=
d
S,
d
E
4 56
where
g
(
m
) is the forward modeling operator for the
seismic and seismoelectric semicoupled problem. It con-
nects nonlinearly the generation of seismograms and
electrograms to the variation of the material properties
of the ground, where
d
is an
N
-vector of the observed
seismic data,
d
S
, and seismoelectric data,
d
E
.The(
N
×
N
)
covariance matrix is given by
π
m d
. The
characteristic of probability density
m d
, like the
mean and the standard deviation or the number of
extrema in the probability density, can therefore be easily
determined. Memory mechanisms of the MCMC algo-
rithms (that keep the chain in the high a posteriori prob-
ability regions of the model space) are responsible for a
greater efficiency of the algorithm in comparison to the
Monte Carlo methods, for which the models are inde-
pendently chosen and tested against the observations.
The basic Metropolis
π
d
=
σ
S
0
0
C
4 57
E
σ
(where S stands for seismic and E for electrical data). This
matrix comprises the measurement errors for both the
seismic and electrical data, which are usually considered
to be uncorrelated and are assumed to obey Gaussian
distributions.
The a priori distribution on the model parameters,
if available, is also assumed to be Gaussian:
Hastings algorithm is a two-step
procedure. In the first step, the current model parameter
vector,
m
, in the Markov chain is modified randomly
to obtain a candidate vector. This candidate is drawn
from a proposal distribution
q
(
m
,
m
) where the choice
of
m
depends on the current vector
m
. The proposal
distribution could be, for example, a multidimensional
Gaussian distribution. In the second step, the candidate
model is accepted with the acceptance probability
(Malinverno 2002):
-
1
P
0
m
=
1 2
M
det
2
π
C
m
1
2
m
T
C
−
m
m
× exp
−
−
m
prior
−
m
prior
, 4 58
where
m
prior
is the prior value of the distribution of
the three petrophysical parameters in the ground and
C
m
denotes the model diagonal covariance matrix
incorporating the uncertainties related to the a priori
model of material properties. In the results, discussed
in Section 4.3.3, we will use a null prior as information
on the model parameters.
In the classical Bayesian approach, model parameters
m
that fit geophysical observations
d
maximizes the
posterior probability density
α
m
;
m
=min 1,
π
m d
q
m m
q
m m
,
π
m d
=min 1,
P
0
m
P
0
m
P
d m
P
d m
q
m m
q
m m
,
m d
. The problem is
to explore the posterior probability density,
π
=min 1, prior ratio likelihood ratio proposal ratio
4 59
m d
,
expressed by Equation (4.54). The denominator of
Equation (4.54) is the normalizing factor required for
the integral of the probability density function to be
π
If the candidate is accepted, the state of the chain
is changed to
m
; otherwise, the chain stays at
m
.