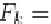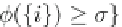Database Reference
In-Depth Information
approach would compare each candidate itemset with every transaction
C
∈
T
to
check for containment. An approach like this would require
O
(
|
T
|·
L
·|
I
|
) item
2
|
I
|
−
comparisons, where the number of non-empty itemsets in the lattice is
L
=
1.
This type of computation becomes prohibitively expensive for all but the smallest
sets of items and transaction sets.
One way to reduce computational complexity is to reduce the number of candidate
itemsets tested for support. To do this, algorithms rely on the observation that every
candidate itemset of size
k
is the union of two candidate itemsets of size (
k
−
1), and
on the converse of the following lemma.
Lemma 10.1 (Downward Closure)
The subsets of a frequent itemset must be
frequent.
Conversely, the supersets of an infrequent itemset must be infrequent. Thus, given
a sufficiently high minimum support, there are large portions of the itemset lattice
that do not need to be explored. None of the white nodes in Fig.
10.1
must be tested, as
they do not have at least two frequent parent nodes. This technique is often referred
to as
support-based pruning
and was first introduced in the Apriori algorithm by
Agrawal and Srikant [
1
].
Algorithm 10 shows the pseudo-code for Apriori-based frequent itemset discovery.
Starting with each item as an itemset, the support for each itemset is computed, and
itemsets that do not meet the minimum support threshold
σ
are removed. This results
in the set
F
1
={
|
∈
{
}
≥
}
(line 2). From
F
1
, all candidate itemsets of
size two can be generated by joining frequent itemsets of size one,
F
2
i
i
I
,
φ
(
i
)
σ
={
|
∈
C
C
F
1
×
. In order to avoid re-evaluating itemsets of size one,
only those sets in the Cartesian product which have size two are checked. This process
can be generalized for all
F
k
,2
F
1
,
|
C
|=
2,
φ
(
C
)
≥
σ
}
, all frequent itemsets
have been discovered and can be expressed as the union of all frequent itemsets of
size no more than
k
,
F
1
∪
F
2
∪···∪
F
k
(line 7).
In practice, the candidate generation and support computation step (line 5) can be
made efficient with the use of a
subset function
and a hash tree. Instead of computing
the Cartesian product,
F
k
−
1
×
≤
k
≤|
I
|
(line 5). When
F
k
=∅
F
k
−
1
, we consider all subsets of size
k
within all
transactions in
. A subset function takes as input a transaction and returns all its
subsets of size
k
, which become candidate itemsets. A hash tree data structure can
be used to efficiently keep track of the number of times each candidate itemset is
T