Writhe, DNA (Molecular Biology)

Writhe is an aspect of DNA structure that concerns DNA topology.

1. Writhing Number

The writhe or writhing number (Wr) is a property of a single closed space curve; in application to DNA, the appropriate space curve is taken to be the duplex axis A. For considerations of DNA structure, the writhe is important insofar as it enters into the fundamental relationship between the linking number (Lk), the twist (Tw), and Wr for a closed circular duplex DNA, Lk = Tw + Wr. Since Wr is calculated only for a closed curve, the quantity is not applicable to nicked circular or linear DNAs. The magnitude of the writhe is directly proportional to n, where n is the number of superhelical turns (see Supercoiling of DNA). For a nicked circular duplex DNA, whose axis on the average lies in a plane, Wr = 0. In all other cases, some of the winding is always converted into changes in Tw, and | Wr| < n.

1.1. The Index Approach

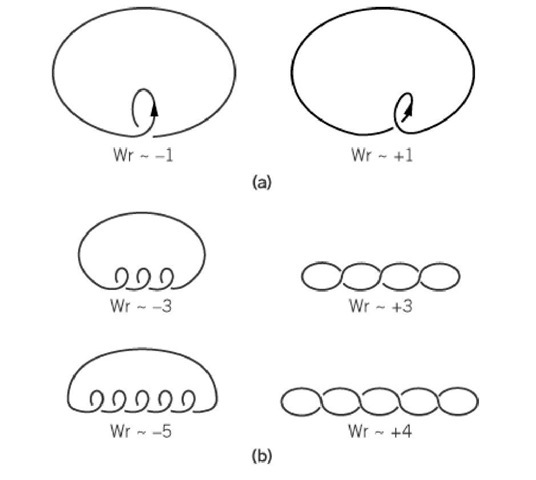
As with the linking number, conceptually the easiest way to calculate the writhe is with the index approach (see Linking Number Of DNA). The axis is assigned an orientation and projected onto a plane. Although a specific orientation must be chosen for the axis in order to calculate the directed writhing number, the actual choice of orientation is immaterial, since a reversal of orientation changes the orientations of both curve segments simultaneously. Some examples are shown in Figure 1. For any given projection, an index number of+1 or -1 is assigned to each crossing of one strand by the other. The index number is negative if the tangent vector to the upper portion of the curve must be rotated clockwise to coincide with the tangent vector of the lower part of the curve. The index number is positive in the opposite case. Since the writhe is not a topological quantity, however, its calculation is not independent of the projection chosen. This serves to distinguish Wr clearly from Lk. The sum of all the index numbers gives the projected writhing number, Wrp, for the DNA axis in the projection chosen.

Figure 1. Examples of calculation of the writhe for some simple curves using the index approach. (a) The writhing number of curves with one coil. In the projections shown, the projected writhe, Wrp, is ±1. However, if the curves are rotated so that other projections are viewed, there are some side views where no crossings are observed. Since Wr requires that all values of the projected writhe be averaged, the actual values of Wr will be slightly greater than -1 in one case and slightly less than +1 in the other case. (b) The extension to curves having multiple coils is straightforward. In the views shown here, the projected writhes are the numbers shown under each curve. As with the loops of one coil, however, some projections will have no crossings, giving rise to values of Wr that are slightly more positive than the negative integers indicated and slightly more negative than the positive integers indicated.

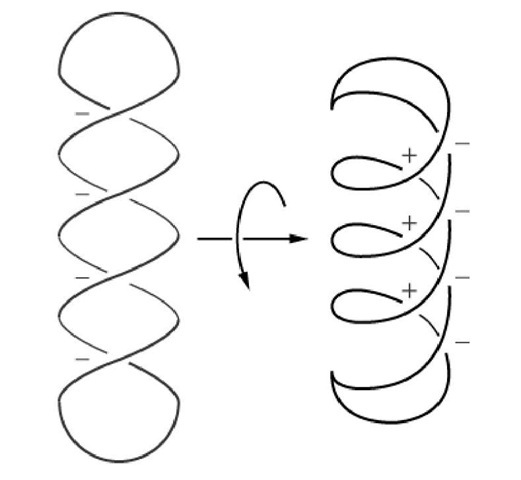
The writhing number, Wr, is obtained by averaging the projected writhing number over all possible projected views. The values of the directed writhing numbers, and hence of Wr, are changed by deformation of the axis. As an example, DNA supercoiled into a regular plectonemic superhelix is shown schematically in Figure 2. In most views, the crossings are all negative and equal in number to the number of supercoils. These have a projected writhe of -n. In some projections, however, positive crossings are also observed. These have a projected writhe more positive than -n. The writhe is the sum of all projected writhes, so it is clear that | Wr| < n. Finally, Wr changes by 2 if the axis is passed through itself once, as happens by treatment with a type II DNA topoisomerase. This is because such a passage converts a +1 crossing to a -1 crossing, a change of -2, or a -1 crossing to a +1 crossing, a change of +2.

Figure 2. Analysis of the projected writhe for an interwound DNA superhelix. The solid curve represents the axis of a cdDNA wound into an unbranched, interwound superhelix. Two views of the same structure are depicted. The view on the left shows only the nodes with negative index numbers, and Wrp = -4. These result from the crossing of distant DNA segments. The view on the right results from rotation about the horizontal axis so that the top of the molecule is tipped toward the observer. This view contains the same negative contributions but contains additional nodes that have positive index contributions, resulting from the crossing of nearby DNA segments. The value of Wrp for this view is thus -1. The Wr is the average of the Wrp values of all views; hence | Wr| is less than the number of supercoils.

1.2. Application of the Gauss Integral

If the trajectory of the DNA axis is known, the writhe may alternatively be calculated from the Gauss integral in a manner analogous to the calculation of Lk (1) (see Linking Number Of DNA):

where T1 and T2 are the unit tangent vectors to the axis curve at any two locations, X1 and X2; r is the distance between the points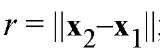; and e; is the unit vector.

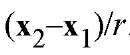1.3. Use of the Surface Linking Number

The third and easiest way to calculate the writhe takes advantage of the fundamental relationship for a closed circular DNA (2), in the form Wr = Lk – Tw. Although this method is indirect, it is considerably easier than the direct methods because both Lk and Tw are much more readily obtained than Wr itself. Even more straightforward is the combination of the fundamental relationship with considerations of surface linking (see Surface Wrapping Of DNA). The fundamental relationship then becomes

The surface linking number, SLk, is simply related to the geometry of the real or virtual surface about which the DNA winds. For the two most commonly encountered cases, SLk = 0 for superhelical DNA having the form of any plectonemic superhelix, no matter how distorted; SLk = ±n for any toroidal superhelix, where the sign is positive for right-handed winding and negative for left-handed winding. Equation (2) then becomes Wr = -STw for a plectonemic superhelix and Wr = ±n-STw for a toroidal superhelix.

The calculation of the writhe therefore reduces to a problem in the calculation of the surface twist. The calculation of STw requires knowledge of the shape of the surface and of the associated path of the DNA axis. If the surface is a protein or other real object, the required information can be obtained, at least in principle, by X-ray diffraction. In the case of a free cdDNA, the axis can sometimes be considered to wrap on a virtual surface. The two most commonly encountered surfaces of this type are the capped cylinder (for plectonemic supercoiling) and the circular torus (for toroidal supercoiling). These are illustrated in Figure 3. For the plectonemic superhelix, STw = n sin(a) for DNA whose axis winds as a regular right-handed superhelix of n turns and superhelix pitch angle a. It follows immediately that Wr = -n sin(a) for a right-handed plectonemic superhelix ( DLk < 0), and Wr = +n sin(a) for a left-handed plectonemic superhelix ( DLk > 0).

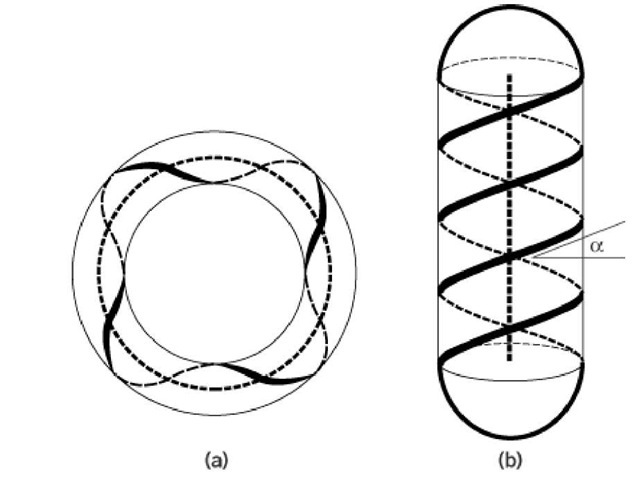
Figure 3. Two types of geometry used in the calculation of the writhe by means of the surface linking number (see Surface Wrapping Of DNA) and surface twist (see Twist, DNA). (a) Toroidal superhelical DNA wrapped on the surface of a virtual torus. The DNA axis wraps +4 times in a right-handed sense on the surface of a torus. SLk = +4. (b) Plectonemic interwound DNA, wrapped on the surface of a virtual capped cylinder. The DNA wraps +2 times up and +2 times down a virtual cylinder, with circular closure at the caps. SLk = 0. The superhelix pitch angle is a.

If the DNA is wound in a regular right-handed toroidal superhelix, SLk = +n. The calculation of STw in this case is more involved than for the plectonemic superhelix and requires knowledge of the dimensions of the virtual toroidal surface on which the DNA is wrapped. If the DNA axis wraps n times around a circular torus of major radius R (distance from the center of symmetry to the central axis of the torus) and minor radius r (radius of the torus), then STw is given by an elliptical integral that must be solved numerically (3). If the torus is highly extended relative to its width, so that, the result is approximately.In the limiting case where r/R o 0, STw is the same as for the plectonemic superhelix. In the other limiting case that r/R o 1, numerical solutions to the elliptical integral must be obtained.

2. Absolute Writhe

The absolute writhe, AWr, is formally similar to the writhe except that the absolute value of the writhe integrand, instead of the usual signed one, is used in the Gauss integral (3). Although it not part of the basic relationship for a topological domain, Lk = Tw + Wr, AWr has the advantage that it is zero if and only if the curve is planar. Indeed, the closer the absolute writhe is to zero the more nearly planar is the curve. This contrasts with Wr, which may be zero even though the curve lies out of plane. For example, any curve that lies on the surface of a sphere has Wr = 0. Such a curve certainly does not have to be planar.

The difference between Wr and AWr may also be understood using the process of projections. If a closed space curve is viewed from a distant point, apparent crossings may be seen by the observer. To each of these crossings is assigned a value of+1 or -1, depending on the orientation of the tangents to the crossing segments. The projected writhe is the algebraic sum of these crossing numbers, and the writhe is the average of all projected writhing numbers over all possible projections. The absolute writhe is defined similarly, but with one major difference: instead of attaching a sign to any crossing, the absolute value of the number of crossings is counted. This number is called the projected absolute writhe. The absolute writhe is the average of all absolute projected writhing numbers over all possible projections. Thus, for a very tightly wound, almost planar figure eight, the writhe may be +1 or -1 depending on the overlay of the crossing segments; but the absolute writhe is always +1.In terms of the Gauss integral, AWr is calculated similarly to
Wr: