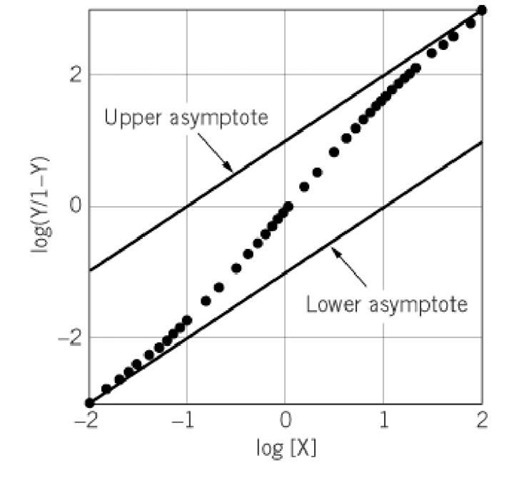
The Hill coefficient is used to provide a quantitative measure of cooperativity of ligand binding. It is usually estimated graphically from a Hill plot. A hypothetical example of a Hill plot is shown in Figure 1. To construct a Hill plot, y, the fractional saturation of the binding sites by a ligand X, is determined experimentally. The data are plotted as log (y/ 1-y) versus log [X]. The Hill coefficient, n H, is given by the slope of this plot at log (y/1-y) = 0—that is, aty = 0.5 or 50% saturation of the X binding sites.
Figure 1. Hill plot. A hypothetical Hill plot for positively cooperative binding of ligand X to a macromolecule with two binding sites for X is shown. The data are presented as points, and the limiting asymptotes with slope 1 at high and low extents of ligand binding are shown as lines. The intrinsic stepwise binding constants, K1 and K2, given by the intercepts at
, are 0.1 and 10, respectively. The Hill coefficient is 1.8.
The Hill plot was initially developed by A. V. Hill in the context of proposing a mechanism for the positive cooperativity of oxygen binding to hemoglobin (1). The central concept of his proposal was recognition that cooperativity in ligand binding requires interactions between multiple binding sites. In the limit that the cooperativity between n binding sites is very strong, then only unliganded and fully n-liganded species of the protein exist.
Analysis of the properties of Equation 4 as a function of [X] shows that the slope approaches +1 at both small and large values of y (2-4). These are shown as the lines in Figure 1 that are labeled lower asymptote and upper asymptote, respectively. As described below, in principle these asymptotes provide information about ligand binding. However, accurate determinations of the asymptotes in practice are difficult because they require measurements at very low and very high extents of ligand binding. For this reason, most uses of the Hill plot focus on the slope at 50% saturation with ligand X, the Hill coefficient.
The Hill coefficient can usually be determined with good precision for cooperative binding systems, and it provides an accurate phenomenological description of the cooperativity. For systems with two interacting binding sites for X (eg, dimeric proteins), it may be possible to determine apparent dissociation constants for each site from the Hill plot (see text below). For larger numbers of interacting binding sites, it may be possible to determine the dissociation constants for the first and last ligands bound and the interaction energy between these sites. However, determinations of dissociation constants for other ligand bindings steps are not in general possible. (See Ref. 3 for discussion relative to oxygen binding to hemoglobin.)
To understand the relations between cooperative ligand binding and the Hill coefficient, it is instructive to consider the case of a symmetrical dimer with one binding site for ligand X on each subunit. The stepwise occupancy of the binding sites can be written
where K ^ and K2 are intrinsic stepwise association constants defined by the equations
The Hill coefficient at y = 0.5 is given by
For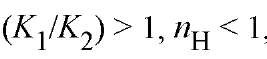
, indicating negative cooperativity. For
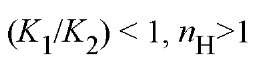, indicating positive cooperativity. The value of n^ cannot exceed 2. The intercepts of the asymptotes in Figure 1, when log [X] = 0 are log K ^ (lower) and log K 2 (upper). Thus they provide values for the intrinsic stepwise binding constants for the initial and final ligand binding steps. Although this is a general result, experimental determination of the asymptotes is in practice difficult. An analogous treatment
Equation 3 can be converted into a form useful for graphical analysis by taking the ratio of bound sites to free sites, y/ (1-y), and taking the logarithm
of cooperativity in the kinetic behavior of a symmetric dimeric enzyme using Weber’s approach of coupling free energies (4) has been presented and shows the relations between the magnitude of the coupling free energies and the value of the Hill coefficient (5). A treatment of the Hill coefficient in the context of the concerted allosteric model is presented on page 135 of Ref. 3 .
