6.7.
Interferometers are optical instruments used for measuring flatness and determining
the length of slip gauges by direct reference to the wavelength of light. The interferometer
incorporates the extension of the application of the optical flat. It overcomes some of the
disadvantages of the optical flats used in ordinary daylight or diffused source of monochromatic
light by having some refined arrangements. In interferometers the lay of the optical flat can
be controlled and the fringes can be oriented to the best advantage. Also there is arrangement
to view the fringes directly from top and above the fringes thus avoiding any distortion due to
incorrect viewing.
6.7.1.
Michelson Interferometer.
This is the oldest type of interferometer, which has
subsequently been modified in several respects and lot of sophistication introduced. However,
Michelson using this interferometer, established exact relationship between meter and red
wavelengths of cadmium lamp ; so understanding of its working will be of interest to all.
The basic Michelson interferometer consists of a monochromatic light source, a beam
splitter and two mirrors. It relies on the principle of constructive and destructive interference
as one mirror remains fixed and the other is moved.
In schematic form, Michelson interferometer is shown in Fig. 6.16, which utilises
monochromatic (or single wavelength) light from an extended source. This light falls on a beam
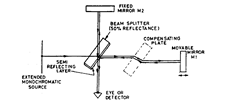
Fig. 6.16. Michelson Interferometer.
splitter (which is a plain parallel plate having a semi-transparent layer of silver at its back)
which splits the light into two rays of equal intensity at right angles. One ray is transmitted
to Mirror M\ and other is reflected through beam splitter to Mirror M2. From both these
mirrors, the rays are reflected back and these reunite at the semi-reflecting surface from where
they are transmitted to the eye as shown in Fig. 6.16.
Mirror Af2 is fixed and the reflected ray from Mi serves as reference beam. Mirror M\
is movable, i.e. it is attached to the object whose dimension is to be measured.
If both mirrors are at same distance from beam splitter, then light will arrive in phase
and observer will see bright spot due to constructive interference. If movable mirror shifts by
quarter wavelength, then beam will return to observer 180° out of phase and darkness will be
observed due to destructive interference.
Each half wavelength of mirror travel produces a change in the measured optical path
of one wavelength and the reflected beam from the moving mirror shifts through 360° phase
change. When the reference beam reflected from the fixed mirror and the beam reflected from
the moving mirror rejoin at the beam splitter, they alternately reinforce and cancel each other
as the mirror moves. Thus each cycle of intensity at the eye represents A/2 of mirror travel.
It may be noted that when monochromatic light source is used then fringes can be seen
over a range of path difference that may vary from a few to a million wavelengths, depending
on the source. However, when white light is used, then fringes can be seen only if both ray
paths are exactly equal to a few wavelengths in total length in glass and air. The lengths
themselves are not important, but only their differences affect fringe formation. So when white
light source is used then a compensator plate is introduced in the path of mirror Mi so that
exactly the same amount of glass is introduced in each of the paths. (In the path of mirror M2,
the glass was coming due to rays passing through beam splitter back surface). The various
sophistications which have undergone to improve the Michelson’s basic apparatus are :
(i) Use of laser as the light source, which means that the measurements can be made
over longer distances ; and also the beam laser compared to other monochromatic sources has
exact and pure wavelength thus enabling highly accurate measurements.
(ii) Mirrors are replaced by cube-corner reflectors (retro-reflectors) which reflect light
parallel to its angle of incidence regardless of retroreflector alignment accuracy.
(Hi) Instead of observing the interference phenomenon by eye, photocells are employed
which convert light-intensity variations in voltage pulses which are processed by electronic
instruments to give the amount and direction of position change.
6.7.2. Single Frequency DC Interferometer System. It is much improved system
over the Michelson simple interferometer. It uses a single frequency circular polarised laser
beam. On reaching the polarising beam splitter, the beam splits into two components, the
reflected beam being vertically polarised light and the transmitted beam being horizontally
polarised light. These two beams referred to as reference arm and measurement arm respec-
tively travel to their retroreflectors and are then reflected back towards the beam splitter.
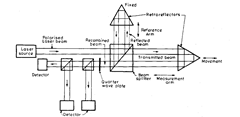
Fig. 6.17. Single frequency DC interferometer.
The recombined beam at beam splitter consists of two superimposed beams of different
polarisation ; one component vertically polarised having travelled around reference arm and
other component horizontally polarised having travelled around the measurement arm. These
two beams being differently polarised do not interfere. The recombined beam then passes
through a quarter waveplate which causes the two beams to interfere with one another to
produce a beam of plane polarised light. The angular orientation of the plane of this polarised
light depends on the phase difference between the light in the two returned beams.
The direction of plane of polarisation spin is dependent on the direction of movement of
the moving retroreflector. The beam after quarter waveplate is split into three polarisation
sensitive detectors. As the plane of polarised light spins, each detector produces a sinusoidal
output wavefrom. The polarisation sensitivity of the detectors can be set so that their outputs
have relative phases of 0°, 90°, and 180°. The outputs of three detectors can be used to
distinguish the direction of movement and also the distance moved by the moving retroreflector
attached to the surface whose displacement is to be measured.
For linear measurements (positional accuracy or velocity), the retroreflector is attached
to the body moving along the linear axis. For angular measurement. For pitch and yaw), the
angular beam splitter is placed in the path between the laser head and the angular reflector.
In this way it is possible to measure flatness, straightness, rotatory axis calibration. Arrange-
ments also need to be made for environmental compensation because the refractive index of
the air varies with temperature, pressure and humidity. Heterodyne interferometer, an a.c.
device avoids all the problems encountered in above d.c. device, i.e. effect of intensity level
change of source, fringe contrast changes and d.c. level shifts which can cause fringe miscounting.
Interferometry is now an established and well developed technique for high accuracy
and high resolution measurement.
6.7.3.
Twyman-Green Specialisation of Michelson Interferometer.
In the Michel-
son interferometer shown in Fig. 6.18, the rays actually describe a cone, giving rise to various
types of fringe patterns which may be hard to interpret.
Twyman-Green modified Michelson interferometer utilises a pin-hole source diaphragm
and collimating lenses. In this way, all rays are rendered parallel to the central rays and thus
all rays describe the same
path. All modern two-beam in-
terferometers are based on
this arrangement. The mir-
rors Mi and M2 are arranged
perpendicular to the optical
axis. If mirror Mi is kept fixed,
and Af2 is moved slowly exact-
ly parallel to itself, the ob-
server will note periodic
changes in the intensity of the
field being viewed, from bright
to dark for every X/2 move-
ment of the mirror. In fact in-
tensity variation is found to be
sinusoidal. It may also be
noted that if one of the mirrors
is even slightly inclined to the
optical axis then parallel fringes will be seen moving parallel to themselves by just one fringe
for every X/2 (half the wavelength of the light source used) mirror motion. Usually it is quite
difficult to count such fringes by eye. However, photo detectors connected to high speed
counters can do this job very accurately (accuracy of one part in million being obtainable). It
is possible to calibrate the output of counter directly in terms of the linear movement of the
mirror M2, but several conditions must be met to achieve these results.
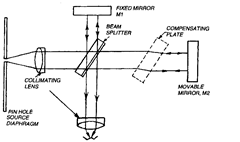
Fig. 6.18. Twyman-Green specialisation of Michelson interferometer.
A simple arrangement of
fringe counting system based on
Roster’s prism is shown in Fig. 6.19.
With the use of Roster’s prism, the
two interfering paths can be ar-
ranged parallel instead of at right
angles. At big advantage of using
Roster’s prism is that if slight vibra-
tions exist, then vibration tends to
affect the arms equally and the an-
noying effect of vibration is nul-
lified. In order to be able to count the
fringes, the following must be taken
care of:
(i) It has been indicated that
mirror should travel exactly paral-
lel to itself and no machines have
ways sufficiently straight to main-
tain uniform fringe fields. The recent trend is to use corner-cube reflectors which are not at all
sensitive to their own orientation and return the reflected ray exactly parallel to the indicident
beam.
(ii) It is observed that the wavelength of light source is modified by the refractive index
of air which is dependent on pressure, temperature and humidity of air (wavelength is fixed
only in vacuum). The slight changes in wavelength may be immaterial in case of flatness or
from measuring systems, but not in fringe counting and gauge block interferometers. So
pressure, temperature and humidity should be measured and correction factors applied for. If
optical paths are longer then the air currents between optical elements exert more and more
influence ; and the system should, therefore, be properly shielded with insulating, and
radiation reflecting enclosures.
(iii) It has already been indicated that the signal strength becomes poor if the path
difference between the rays corresponding to two mirror systems is high. Thus it limits the
range of movement of movable mirror because its movement means change in path length. It
is found that using cooled mercury 198 lamps, speeds of 12.5 mm/sec. are possible when path
lengths are nearly equal, but the traversing speed has to be reduced to 0.0025 mm/sec, when
path difference is about 250 mm due to poor signal to noise ratio.
Two methods are possible to improve
the situation, (a) Use laser source (A.C. laser
interferometer described later). (6) Couple a
suitably designed Fabry-Perot etalon with a
Twyman-Green interferometer ; and then it
is possible to attain 6 m path difference with
good contrast. The use of Fabry-Perot etalon
in shown in Fig. 6.20. The etalons are made
up of two optical flats (flat to 1/20 fringe or
better) and coated with a high efficiency
semitransparent film on the two facing sur-
faces (as shown in Fig. 6.20). These flats are
kept exactly parallel by means of a carefully
designed spacer. In this interferometer
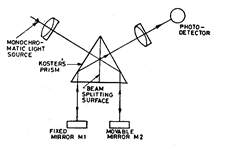
Fig. 6.19. Fringe counting Interferometer
based on Roster’s Prism.
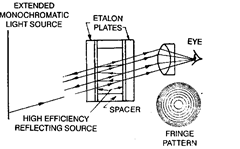
Fig. 6.20. Fabry-Perot Interferometer.
observer will see a series of very sharply defined bright circles resulting from interference
between rays that are multiply reflected between the two working faces of the etalon.
(iv) These high sensitivity interferometers are highly susceptible to vibration. The
presence of vibration may either wash out the fringes completely or may be very annoying for
the observer. As already indicated, the use of Roster’s prism can reduce the problem of
vibration to great extent.
(v) In order to be able to count the fringes corresponding to both forward and backward
movements, two detectors, one focussing the dark fringe and other focussing the adjoining
bright fringe, must be arranged; i.e. two detectors should be aligned with respect to the fringes,
one located 90 fringe phase degree with respect to the other. If fringe position is to be detected
to less than 1/4 fringe, then three photodetectors must be arranged to look at fringe sections
120° out of phase with each other.
6.7.4.
N.P.L. Flatness Interferometer.
This instrument, as the name suggests, is
mainly used for checking the flatness of flat surfaces. This interferometer was designed by
National Physical Laboratory and is commercially manufactured by Hilger and Watts Ltd.
The flatness of any surface is judged by comparing with an optically flat surface which is
generally the base plate of the instrument. This instrument essentially consists of a mercury
vapour lamp (Fig. 6.21). As we are interested in having single monochromatic source of light,
the radiations of the mercury lamp are passed through a green filter. The wavelength of the
resulting monochromatic radiation is of the order or 0.0005 mm. This radiation is then brought
to focus on pinhole in order to obtain an intense point source of light. A mirror is used in order
to deflect the light beam through 90°. The pinhole is placed in the focal plane of a collimating
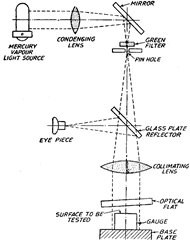
Fig. 6.21. NPL flatness interferometer.
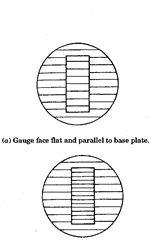
yo) Gauge face flat but not parallel to base plate.
Fig. 6.22
lens, thus the radiations out of the lens will be parallel beam of light. This beam is directed on
the gauge to be tested via an optical flat. The fringes formed are viewed directly above by means
of a thick glass plate semi-reflector set at 45° to the optical axis.
The gauge to be tested is wrung on the base plate whose surface is finished to a degree
comparable to that of the highest quality gauge face. As the optical flat is placed above it in a
little tilted position, interference fringes are formed; one between rays reflected from the under
surface of the optical flat and those reflected from the surface of the gauge, and the other
between rays reflected from the under surface of the optical flat and those reflected from the
base plate.
If the gauge face is flat and parallel to the base plate, then the optical flat being equally
inclined on both the surfaces the fringe pattern from both the gauge face and the base plate
will consist of straight, parallel and equally spaced fringes as shown in Fig. 6.22 (a). When the
gauge is flat but not parallel to the base plate, then straight and parallel fringes of different
pitch above the gauge face as compared with those of the base plate are seen [Fig. 6.22 (b)].
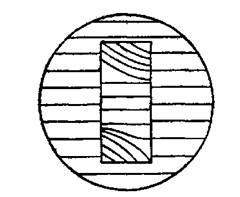
Fig. 6.23. Surface of gauge
is inclined to base plate.
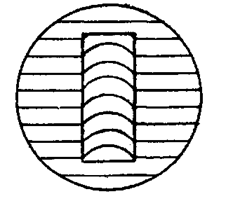
Fig. 6.24. Gauge surface
convex/concave.
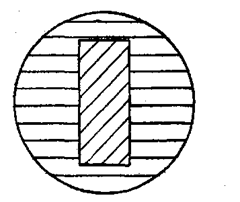
Fig. 6.25. Slight rounding off
at corners.
In such case, to determine the amount of unparallelism, provision is mkde to rotate the
base plate by 180° and this method is covered in detail after discussing the various other
possible cases.
In case taper is present in some other direction, i.e. surface of the gauge is flat but its
surface is inclined to the base plate at some other angle, then fringe pattern obtained is as
shown in Fig. 6.23. Here the error is indicated by the amount by which the fringes are out of
parallel with those on the base plate. When the gauge surface is convex or concave then fringe
pattern as shown in Fig. 6.24 is obtained, i.e. the fringes on the gauge are curved lines.
Slight rounding off at the corners of
an otherwise generally flat and parallel sur-
face will give a fringe pattern as shown in
Fig. 6.25 having closely curved lines at the
ends, and straight and parallel fringes of
equal pitch in the middle.
6.7.5.
Quantitative Estimate of Error in Parallelism.
The base plate on
which the gauge is placed, is of rotary type
and can be rotated at any angle. The under-
side of the gauge is lapped truly parallel
with the working surface of the base plate.
Now if a non-parallel gauge is viewed, the
angle which it makes with the optical flat
will be as shown in Fig. 6.26. In this posi-
tion, face AB is nearly parallel with the
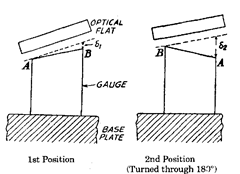
Fig. 6.26. Determining error in parallelism.
optical flat and distance bi can be estimated by counting the number of fringes formed or the
surface of gauge. If the table is turned through 180°, the surface BA will then be less parallel
with the optical flat and a greater number of fringes will be observed. Let the number of fringes
in first case be ATi and in second case AT2.

6.7.6.
The Fitter—N.P.L. Gauge Interferometer.
This is also called the gauge length
interferometer and used for determining actual dimensions or absolute length of the gauges.
As the mechanical sub-division of end standards length tends to be laborious when small
lengths are considered, and due to liability of error in that method, direct measurement
interferometer based on the design of N.P.L. is most commonly used.
Since this involves very precision work, it is important to see that the physical conditions
surrounding the measuring equipment are standardised and controlled. The standard condi-
tions being temperature of 20°C, barometric pressure of 760 mm of mercury with water vapour
at a pressure of 7 mm and containing 0.33% by volume of carbon dioxide. In case conditions
are different, then correction factors have to be applied.
The diagrammatic arrangement of the instrument is shown in Fig. 6.27. S is suitable
source of light and light form it is brought to focus on the illuminating aperture in the plate
by passing it through a condensing lens. This plate is placed at the focal plane of a collimating
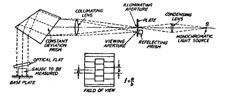
Fig. 6.27. Pitter—NPL gauge interferometer.
lens. Thus light from this plate acts as a point source of light and after collimating lens, rays
of light in the form of parallel beam of light move into a constant deviation prism. The constant
deviation prism disperses the light into its constituent colours. The beams of different colours
are thus reflected downwards by the prism in slightly different directions. In case of cadmium
source of light, the various colours of beam available are red, green, blue and violet. Any one
of these coloured beams can be directed vertically downward on the gauge and the base plate
through the optical flat by slightly rotating the constant deviation prism about a certain axis.
The rays reflected at the gauge face and at the face of the base plate return along the same
path approximately as the incident rays, but their axis is tilted slightly due to inclination of
optical flat and thus brought to focus at some other point on the plate, where they are incident
on a reflecting prism. Reflecting prism then reflects the
rays into the eyepiece at normal to these rays.
The fringe pattern obtained is shown in the field
of view in Fig. 6.27. Actually two interference systems
are produced. One set of fringes is due to the upper
surface of the gauge and the other is due to the base
plate’s reflecting surface. It is essential that the gauges
being calibrated by this method possess a very high
degree of flatness and parallelism. Only then the fringe
pattern from the gauge and the base plate will consist
of straight, parallel and equally spaced fringes of the
same frequency. Generally two fringe patterns cannot
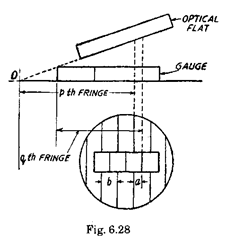
be in phase and will be displaced as shown in Fig. 6.28.
The amount of this displacement varies for each colour
and, therefore, wavelength of light used. The displace-
ment observed a, is expressed as a fraction of the fringe spacing b, i.e. ‘f = alb. In order to
determine the length of the gauge an estimation of f is made for each of the four radiations
from the cadmium lamp.
As the two surfaces, i.e. surface of the gauge and of the base plate, are perfectly flat and
parallel, the wedge shaped air film is of same angle in both the cases. Let the lower surface of
the optical flat be produced to meet the base plate surface line produced at O. Let anywhere
in the middle of the fringes system, a pair of fringes be chosen. Let pth. be the fringe on base
plate and q’th on the gauge.
![]()
where /”is the fraction alb and N is the difference of the fringes p and q. Obviously the value
of N will be very large and also complete number as p and q are full integers.
Before proceeding to estimate length upto fifth and sixth decimal place, it is essential
that length of the gauge be determined accurately as far as possible by other methods.
Let the observed fractions for three different wavelengths be flt f2 and and the
corresponding integers, i.e. full number of fringes be N\, N2, N3 respectively for lights of
wavelengths \i, ^.3, respectively.
Since the height of the gauge is same,
![]()
The nominal height of the gauge is known to us as told previously. For nominal height,
the fractions will be different and they can also be calculated by knowing the wavelengths of
lights.
e.g. for red light, wavelength is 25.348478 n in.
and for green light, wavelength is 20.023055 \JL in.
and for violet light, wavelength is 18.418017 \i in.
Thus if nominal length be 0.3″, then by calculation, the fractions will be 0.06, 0.46, 0.46
respectively. Let these fractions obtained by calculation be denoted by/i’, f2′, fa and the number
of whole half wavelengths in nominal length be ‘, N?’, N* respectively.
![]()
Now the difference between the actual length of the gauge arid the nominal length will
be
![]()
It is very obvious that in the above expression, iVj -iVy, N2-N2′,N3-N3 will be a whole
number as N, N’ themselves are whole numbers and also it will be relatively small number.
.-. Equation (1) can be solved by hit and trial by substituting the values of Ni – Ni, N2
-N2′, N3 – N3 as 1, 2, 3, etc. [ku h^, k3, fu f2, f3; f{, f2, f3, etc., in Eq. (1) are known]. Once this
equation is solved, then length of gauge can be calculated. However this is a laborious job to
solve this equation by hit and trial method. In order to make calculations easy, a special slide
rule is made in which there are four scales and the wavelengths of red, green and violet
radiations are set out to scale from a common zero. The lower scale has values corresponding
to micro-inches. One cursor having one straight vertical line is also incorporated.
To solve equation (1) by this slide rule, since the values of fractions /i — fx, f2 -f2′,f3 -
f3′ are known and it is known that values of Ni – N{ etc., will be whole integer we try to locate
the vertical line of cursor at such a place where the three fractions coincide approximately and
the error between nominal value and actual value will be directly read from bottom line. (Also
refer solved questions at the end of this chapter for further clarity).
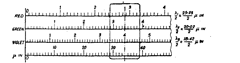
Fig. 6.29. Special Slide Rule for use with N.P.L. gauge Interferometer.
6.7.7.
Total Phase Correction.
When an incident ray is reflected from optically
finished glass or quartz, there is no
(zero) phase shift. But when it is
reflected from steel gauge block, then
incident light undergoes a phase change
and appears to “penetrate” the surface,
reflecting from a point below what might
be called its mechanical surface (Refer
Fig. 6.30). The correction factor varies
from one material to another and it also
varies with surface finish. In perfectly
lapped steel, the phase change correc-
tion amounts to approximately 0.00002
mm.
Depending on surface finish, the
total phase change correction may
amount to 0.00007 mm for gauge blocks.
Further wringing film thickness
of the order of 0.000006 mm also needs
to be accounted for. An improper wring
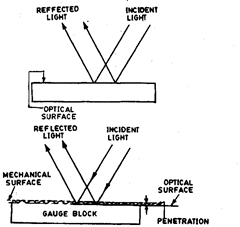
Fig. 6.30. Phase correction.
may easily result in a value many times more than this amount. The thickness of film also
depends on the type of materials in contact, their flatness and surface finish.
