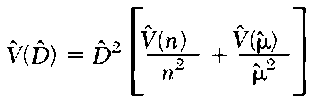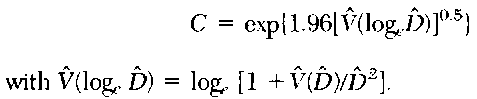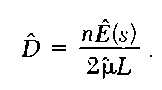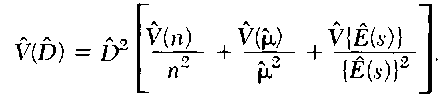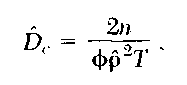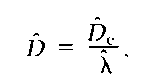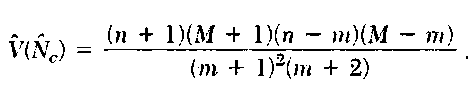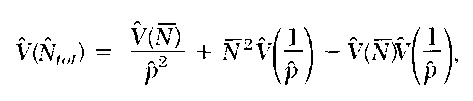Abundance estimation covers the range of techniques by which the size of a population of marine mammals can be estimated. Such population size estimates are often referred to as “absolute” abundance estimates. When it is difficult to estimate absolute abundance with an acceptably low bias, relative abundance indices are often used instead. These are indices that are believed to be proportional to population size, apart from stochastic variation, allowing trends in the population in space and/or time to be assessed. The main techniques for abundance estimation (relative or absolute) are distance sampling, inark-recapture, migration counts, and colony counts.
I. Distance Sampling
Distance sampling (Buckland et al., 1993) is the most widely used technique for estimating the abundance of animal populations. Because it is particularly suited to populations of animals that are readily detectable (at least at close quarters) and sparsely distributed over a large area, it is unsurprising that the methods are widely used by marine maininalogists. Indeed, most of the innovative developments in distance sampling in the last two decades have arisen through applications of the methodology to cetaceans. Distance sampling has also been applied on several populations of ice seals.
The two primary methods of distance sampling are line transect sampling and point transect sampling. The latter method has never to our knowledge been applied to marine mammal populations, and we therefore concentrate mostly on line transect sampling. Another distance sampling method is cue counting, which was developed specifically for populations of large whales, and the theory for which is closely similar to that for point transects. Distance sampling data may be analyzed using software Distance (Thomas et al., 1998).
A. Line Transect Sampling
1. Survey Design In line transect sampling, the survey design comprises a set of straight lines, spanning the full study area for which an abundance estimate is required. For marine mammal smveys, the lines are covered by a team of observers on a ship or boat or by one or more observers in an aircraft. The methodology requires that lines are randomly placed in the study area or that a grid of systematically spaced (i.e., equally spaced) lines is randomly located in the area. Because efficiency is improved if lines are placed perpendicular to density contours, a common design for inshore surveys is to have a series of parallel lines, randomly spaced or more usually systematically spaced, as far as possible perpendicular to the coastline. The study area is often divided into geographic blocks or strata, allowing different orientations of the grid of lines in different strata and allowing effort to be greater in high-density strata. For shipboard surveys especially, systematic zig-zag designs are often used because there is then no loss of expensive ship time in traversing off-effort (i.e., not searching for marine mammals) from one line to the next. The ship can then be continuously searching for marine mammals during daylight hours.
2. Assumptions The following three assumptions should hold:
1. Animals on or very close to the line are certain to be detected (but see later).
2. Animals are detected before they respond to the presence of the observer, and nonresponsive movement is slow relative to the speed of the observer.
3. Distances are measured accurately (for ungrouped distance data), or objects are correctly allocated to distance interval (for grouped data).
Bias from nonresponsive movement is generally negligible, provided that the average speed of the animals is less than one-half of the speed of the observer. A fourth assumption is made in many derivations of estimators and variances: whether an object detected is independent of whether any other object is detected. Point estimates are robust to the assumption of independence, and robust variance estimates are obtained by taking the line to be the sampling unit, either by bootstrapping lines or by calculating a weighted sample variance of encounter rates by line.
We do not need to assume that animals are randomly distributed throughout the survey area, provided that lines are placed randomly with respect to the animals. This ensures that objects in the surveyed strip are uniformly distributed with distance from the line.
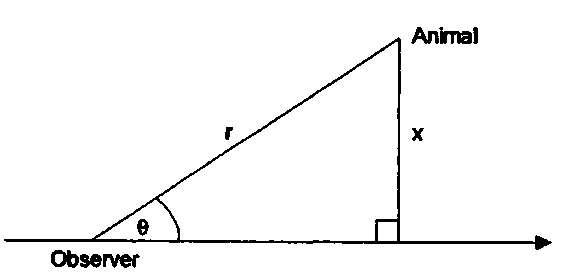
3. Estimation Perpendicular distances x are measured from the line to each detected animal. (We will consider the case that animals occur in groups later.) In practice, for shipboard surveys, detection distances r and detection angles 0 are usually recorded, from which perpendicular distances are calculated as x = r sin(0) (Fig. 1). Suppose there are k lines of lengths /], . . . , (with Xlj = L), and ri animals are detected, at perpendicular distances A],.. ., x„. Suppose that animals further than some distance iv from the line are not recorded. Then the surveyed area is a = 2wL, within which n animals are detected. However, not all animals within the surveyed area are detected. Let the effective half-width of the strip be (jl < it’ (so that the proportion of animals within the surveyed strip that are detected is \jJw). Then animal density (number of animals per unit area) is estimated by
Abundance is estimated as N = AD, where A is the size of the study area. We therefore need an estimate ji of |x. The software Distance provides comprehensive options for these analyses.
4. Variance and Interval Estimation The variance of D may be approximated using the delta method, assuming no correlation between n and p,:
The variance of n is generally estimated from the sample variance in encounter rates, n/lj, weighted by line lengths /,. When p, is estimated by maximum likelihood, its variance is estimated from the information matrix.
Figure 1 The observer records an animal at detection distance r and detection angle 0, from which the perpendicular distance is calculated as x = r sin(Q).
If we assume that D is log-normally distributed, approximate 95% confidence limits are given by (D/C, DC) where
Often, bootstrap variance and interval estimation are preferred. Resamples are usually generated by sampling with replacement from the lines so that independence between the lines is assumed, but independence between detections on the same line is not.
5. Estimation When Animals Occur in Clusters Animals often occur in groups, which we term “clusters.” If one animal in a cluster is detected, it is assumed that the whole cluster is detected, and the position of the cluster is recorded. Equation (1) then gives an estimate of the density of clusters. To obtain the estimated density of individuals, we must multiply by an estimate of mean cluster size in the population, E(s):
The corresponding variance estimate is
Because the probability of detection is often a function of cluster size, the sample of cluster sizes exhibits size bias. In the absence of size bias, we can take E(s) = s, the mean size of detected clusters. Several methods exist for estimating E(s) in the presence of size bias (Buckland et al, 1993).
The just-described methods assume that once a cluster of animals is detected, it is possible to record the size of that cluster accurately. For shipboard and aerial surveys, this often dictates that at least part of the survey is conducted in “closing mode.” After detection, search effort ceases, and the vessel closes with the detected cluster, to allow more accurate estimation of cluster size. This strategy also eases the difficulties of species identification. If “passing mode” is adopted, then underestimation of the size of more distant clusters might be anticipated. Regression methods for correcting size bias also correct for this bias, provided that the sizes of clusters on or close to the transect line are estimated without bias. Where cluster size estimation is problematic, observer training is usually necessary to ensure that bias is not large.
6. Estimation When Detection on the Line Is Not Certain The standard line transect method assumes that animals on the line are certain to be detected. Double-platform methods in which observers search simultaneously from two platforms are therefore becoming commonplace. This allows extension of the standard methods to the case that animals on the line are not certain to be detected and also, given appropriate field methods, allows adjustment for responsive movement of animals prior to detection. Several researchers have made advances in developing methodology for analyzing such data, notably Borchers et al. (1998). Their method uses Horvitz-Thompson-type estimators and also yields a unified approach to the analysis of line transect data in which animal density is estimated in a single step, which contrasts with the conventional strategy of independently estimating the three parameters: encounter rate, effective strip width, and mean cluster size. Double-platform surveys are used widely in cetacean surveys and have also been used for estimating the abundance of polar bears (Uisus imritiimis).
7. Current Areas of Research Active research topics likely to become available shortly in software Distance include spatial modeling of line transect data; integrated analysis of double-platform data; general methods for incorporating covariates in analyses; automated survey design algorithms; and adaptive line transect sampling.
B. Strip Transect Sampling
Strip transect sampling is a special case of line transect sampling in which it is assumed that all animals out to the truncation distance w are detected. This simplifies analysis, and distances of detected animals from the line need not be measured, except to ensure that they are within distance it’ of the line. However, the method is seldom efficient for marine mammals; if the strip is narrow enough to ensure that all animals out to are detected, then many animals are detected beyond tv, and these observations must be ignored. Abundance of sirenian populations has traditionally been obtained by strip transect methods.
C. Cue Counting
In cue counting, observers on a ship or in an aircraft cover a sector ahead of their observation platform and record all cues detected within the sector and the distances of the cues from the platform. In principle, the method can be used for any marine mammal, but in practice, it has been used primarily for large whales, for which the cue is the blow. The same design considerations apply as for line transect sampling, although the analysis is essentially the same as for point transect sampling.
If cues are well defined (as blows of large whales are), then cue counting has the advantage over line transect sampling that the recording unit is the individual cue. Observers need not identify whether different cues are from different animals or how many animals are in a cluster. It also does not matter if some whales stay down so long that they will be undetectable even if they are on the transect line, provided that all cues within the recording sector and very close to the observation platform are detected. Another advantage is that the method requires observer-to-animal distances, which are easier to estimate than perpendicular distances of animals from the line. The main disadvantage is that the method yields estimates of cue density per unit time, which can only be converted into whale density by estimating the cue rate from additional costlv surveys. The estimated cue rate is prone to bias, both because animals may behave differently when a survey ship is close by and because it is easier to monitor animals that cue frequently, thus biasing the cue rate upward. Additionally, if animals cue more frequently when a ship is bearing down on them, an excess of short distances will be observed in the distance data, biasing the estimation of cue density.
The number of cues per unit area per unit time is estimated by
where n is the number of cues detected in time T, <)> is the angle of the sector in radians, and p is the estimated effective radius of detection. Estimated density is then
where X is the estimated number of cues per animal per unit time (the cue rate). As before, abundance is estimated as N = AD. where A is the size of the study area.
Because cues may be from the same whale, or the same pod of whales, tliev cannot be assumed independent. However, this is not a problem given the robust variance estimation methods provided by software Distance.
If cues immediately ahead of the vessel might be missed, double-platform methods similar to those for line transect sampling may be used. This has the advantage over those analyses in that it is easier to identify whether a single cue is seen from both platforms, e.g.. by recording exact times of cues, than to identify whether a single animal or animal cluster is seen by both platforms, as the two platforms may see different cues fiom the same animal.
II. Mark-Recapture
Mark-recapture tends to be more labor-intensive and more sensitive to failures of assumptions than distance sampling. However, it is applicable to some species that are not amenable to distance sampling methods and can \ield estimates of survival and recruitment rates, which distance sampling cannot do. Mark-recapture methods can be useful for populations that aggregate at some location each year, whereas distance sampling methods are more effective on dispersed populations. They should therefore be seen as different tools for different purposes. Among marine mammals, mark-recapture has been used most often to estimate the abundance of pinnipeds, usual!}’ for the estimation of voung of the year. Polar bears have also been the subject of mark-recapture studies. Perhaps the most comprehensive software currently available for analyzing mark-recapture data is MARK (White, 1999).
A. Estimation from a Tagged Subset of Animals
1. The Petersen Estimator In its simplest form, mark-recapture consists of marking a sample of M animals from a population of unknown size N, returning the animals to the population and then removing, capturing, or observing a sample of n animals. Suppose that, of these n animals, m were marked. We assume that the proportion of marked animals in the second sample is a valid estimate of the proportion of marked animals in the population, giving the following “Petersen” estimate of population size: N = nM/m.
2. Chapman’s Modified Estimator Inference for this model is complicated by the fact that the variance of N is infinite unless n + M > N, in which case in cannot be zero. Chapman’s estimator Nc = (n + 1 )(M + l)/(m + ]) — 1 has a lower bias (and no bias for n + M > N), provided that the assumptions of the estimator are satisfied. It has variance
Many variations on this theme have been developed, including extensions to multiple samples, extensions to open populations, “single release” methods, and “single recapture” methods (particularly suited for when the mark is recovered from a dead animal). We make no attempt to cover these methods here, but refer the reader to Seber (1982).
3. Assumptions The assumptions required for N to be a reasonable estimate of population size are that the population of interest is closed over the survey period and that animals are marked and resighted or recaptured at random. In using the ordinary Petersen estimate, it is also assumed that marks are not lost during the survey period and that marking does not affect the probability of resighting or recapturing the animal. Methods have been developed to circumvent these assumptions and the literature for this topic is rich (e.g., Otis et al., 1978; Pollock, 1990). For most wildlife populations, probabilities of recapture or resighting tend to vary among animals for a variety of reasons. This heterogeneity can be problematic to model and can lead to a large bias in abundance estimates, so that the design of a mark-recapture survey should be carefully addressed to minimize heterogeneity.
4. Estimation of Pinniped Numbers by Mark-Recapture Mark-recapture techniques have been successfully used to estimate the abundance of young of the year for several species of fur seals. Chapman and Johnson (1968) described the first successful application of this technique for the population of north-em fur seals (Callorhinus ursinus) oil the Pribilof Islands. They marked seals by shearing some hair from their heads and later went back to the colony and counted numbers of marked and unmarked animals within groups of animals. They calculated a Petersen estimate of abundance, which they verified on small colonies where direct counts of young of the year could be made. Resighting was replicated on each colony and several procedures for estimating the variance of the total population size were investigated. These included (1) an empirical estimate calculated as the variance of the mean of replicated estimates for each colony, and the variance of the total calculated by summing the individual colony variances, and (2) a variance for each replicated colony estimate assuming the hypergeometric distribution, with the variance of the mean count for each colony estimated from the variances of the individual counts. They also discussed the use of interpenetrating subsamples to estimate the variance. This procedure is similar in flavor and intent to the bootstrap procedure.
5. Mark-Recovery Methods Before the development of line transect methods for estimating the size of populations of large baleen whales, inark-recovery studies were carried out in which “Discovery” marks were fired into whales, a proportion of which would later be recovered by whalers. Disadvantages of this approach included a requirement for very large sample sizes to ensure an adequate number of recaptures; a long delay before sufficient data accumulated to allow abundance to be estimated; and strong sensitivity of abundance estimates to failures of assumptions. The methods were largely unsuccessful. For a review of the mark-recapture models that are potentially relevant to such data, and of the numerous sources of potential bias in the abundance estimates, see Buckland and Duff (1989). Before the development of mark-recapture or mark-re-siglit techniques for northern fur seal pups, there were many attempts to estimate the population size by tagging pups at birth and recovering the tags in a commercial harvest. This application failed for similar reasons that the use of Discovery tags failed to properly estimate the size of cetacean populations.
B. Use of Natural Markings
Studies that use natural markings to identify individual animals in a population have become widespread in recent years. These usually rely on photo identification of individuals. A significant milestone in the use of such methods was Hammond and colleagues (1990), which comprises an edited collection of papers from a workshop on the topic. While the technique is undoubtedly of great value, it is important to be aware of its limitations.
Natural markings data can be very effective for estimating survival rates of marine mammals. Abundance estimation is more problematic, as this involves extrapolation from the identified subpopulation. If a high proportion of the population (>80%) can be identified, then abundance estimates are likely to have small bias, especially as there is a tendency to underestimate population size. It is possible to achieve such high rates, e.g., for small coastal populations of bottlenose dolphins (Tursiops truncatus) and pinniped colonies, provided individuals have distinct markings. The method is then useful because it allows enumeration of almost the whole population without fear of double counting individuals or of seriously underestimating population size. When smaller proportions of animals are identified, estimates of population size can be badly compromised for a variety of reasons. Severe heterogeneity in the “capture” probabilities is common, e.g., because some natural markings are identified much more readily than others or because some individuals are more approachable than others. It is notoriously difficult to model such mark-recapture data reliably. Another problem is that the population being estimated is not always well defined, with some animals from elsewhere temporarily entering the population and others temporarily absent. A severe problem for large populations, in which only a small proportion can be identified, is that false positives in the matching procedure, even if they occur only rarely, can lead to a substantia] underestimation of population size. Genetic fingerprinting, if feasible, can reduce this problem substantially.
Natural markings studies are invaluable for estimating survival and birth rates, for migration routes, and for detailed studies, including abundance estimation, of a small population. However, they are rarely a cost-effective or reliable method for estimating the size of large populations of marine in animals. Given the current research interest in this topic, especially for estimating abundance of feeding or breeding aggregations of humpback (Megaptera novaeangliae), blue (Balaenoptera musculus), and right whales (Eubalaena spp.), further advances can be anticipated that will widen the applicability of the methods.
III. Migration Counts
Many populations of large whales conveniently file past coastal watch points on migration, allowing observers to count a large proportion of the population. This count can then be corrected for animals passing outside watch periods to estimate population size. In practice, further corrections are needed, e.g., to adjust for pods that pass undetected during watch periods, for biased estimation of pod size, for different rates of passage between day and night, and for a component of the population that fails to pass the watch point. Despite the need for various correction terms, migration count data yield very precise estimates of abundance with low bias, provided that the more significant correction factors are estimated reliably. This is unsurprising given that typically 30^10% of the population might be seen by the observers, a much higher fraction than is normal in a distance sampling survey.
The methods usually used for modeling migration counts were developed for the analysis of surveys of the California gray whale (Eschrichtins robustus). To estimate numbers of undetected pods passing during watch periods, two count stations operate independently, and these double-count data are modeled using logistic regression. A polynomial model is used to estimate the rate of passage as it varies through the season, from which numbers of whales passing outside watch periods are estimated. A Bayesian approach is used for analyzing similar data on bowhead whales (Balaena mysticetus).
IV. Colony Counts
Many populations of pinnipeds gather for breeding and pupping at certain times of the year. Researchers often make counts of these populations from cliffs above the colonies, from planes flying overhead, or sometimes from ships passing the colony. Often photographs are taken of the colonies. These are brought back to the laboratory for analysis and form a permanent record of the population. In most pinniped populations, it cannot be assumed that all the animals are on shore at any given time, although in fur seal populations, there is a time window in which almost all of the young of the year and breeding males are present, and in certain phocid populations all the young of the year and breeding females are present. Thus, colony counts alone cannot be used to determine absolute abundance of the population size, except for certain classes of animals, and this depends on the reproductiv e patterns of the population of interest, which must be taken into account when the survey is designed. Serial colony counts can be used to determine the rate of increase of the population if the same proportion of animals is present each year at the colony when the counts are made. This assumption is most likely valid for young of the year. For other segments of the population, this assumption fails if the timing of reproduction changes or if conditions at sea change so that animals need to spend a different amount of time at sea feeding and consequently a different amount of time at the colony.
The size of the harbor seal (Phoca vitulina) population in the state of Washington is estimated by combining colony counts made during aerial surveys and mark-recapture to account for animals not present during the aerial surveys. Transponder tags with unique frequencies are attached to animals before the surveys. During the flyovers, animals 011 shore are counted and radio searches are made to determine the proportion of animals that is ashore. The total population is estimated as Ntot = N/p where N is the average count of animals on shore andp is the estimated fraction of marked animals 011 shore. The variance of N,„, is estimated as
where V(N) = s2/n , with s2 equal to the sample variance of the n counts, and V(l/p) = V(p)/p4 = (1 – p)!Mp3 , with M equal to the number of marked animals.
A corrected count method is also used to estimate numbers of southern elephant seal (Mirounga leonina) and fur seal pups (Arctocephnlus gnzelln) on South Georgia. In those surveys, counts of adult females are made from shore or ship along the whole coastline during the pupping season. The counts made at any particular site are then used to estimate the total production for that site based 011 the adult female haul-out curves and pregnancy/pupping rate estimates from sites that are monitored regularly (twice daily in the case of fur seals) through the breeding season. Similarly, the abundance of northern fur seal pups on the Pribilof Islands is sometimes estimated from inark-recapture estimates 011 sample colonies coupled with counts of breeding males on all colonies (York and Kozloff, 1987). The ratio of pups to breeding males, estimated on the sampled rookeries, is multiplied by the total count of breeding males 011 all colonies.
The sizes of colonies of pinnipeds can also be determined using estimates of the area of all colonies coupled with estimates of the density of animals 011 those colonies. Although this method is often used to estimate the sizes of bird colonies, it has only been used occasionally to estimate pinniped population sizes. The estimates of the areas of the colonies were made from maps of the colonies. Counts 01″ corrected counts, or mark-recapture estimates of the population of interest, are determined 011 a subsample of colonies. It is assumed that the density of animals in the sampled colonies is representative of the density 011 all colonies and that the total population is estimated by multiplying the total area by the estimated density. Researchers attempted to use this method to estimate the size of the Pribilof northern fur seal population in the late 1940s. At that time, it was thought that the variability of the estimates was too large and efforts were begun to design inark-recapture studies.
Counts, or more often corrected counts, are also sometimes attempted on other marine mammals. For example, because sea otters (Enhydrn lutris) are difficult to survey by other means, they tend to be counted from a boat. Such counts typically underestimate population size, sometimes substantially so (Udevitz et al, 1995).