Uncertainty in Remote Sensing and GIS : Fundamentals Part 2

Accuracy Assessment

The methods discussed so far for predicting the prediction error (e.g. SE of the mean) have been model-based. Thus, they depend on model choice (the particular model chosen and fitted). Approaches for assessing the accuracy of predictions based primarily on data and, in particular, an ‘independent’ testing data set (i.e. data not used to fit the model and estimate its parameters) are now considered.

Retrieval, verification and validation

Before examining accuracy assessment it is important to highlight the misuse of some terms. First, it is common, particularly in the literature relating to physical modelling, to read of parameters being ‘retrieved’. This term is misleading (implying that a parameter is known a priori and that it has somehow been lost and must be ‘fetched’ or ‘brought back’). Parameters are estimated. Second, it is common in the context of accuracy assessment to read the words ‘verify’ and ‘validate’. To verify means to show to be true (i.e. without error). This is rarely the case with modelling in statistics and even in physical modelling (strictly, verification is scientifically impossible). No one model is the ‘correct’ model. Rather, all models compete in terms of various criteria. One model may be the preferred model in terms of some criterion, but nothing more. For example, if we define the RMSE as a criterion on which models are to be judged, then it should be possible to select a model that has the smallest RMSE. However, this does not imply that the selected model (e.g. simple regression) is in any sense ‘true’.

To validate has a similar, although somewhat less strict meaning (it is possible for something to be valid without being ‘true’). Its use is widespread (e.g. in relation to remote sensing, researchers often refer to ‘validation data’ and physical models are often ‘validated’ against real data). This use of the word validation is often inappropriate. For example, we do not show a classification to be valid. Rather, we assess its accuracy. In these circumstances, the correct term is ‘accuracy assessment’, and that is the subject to which we now return.

Once a model has been fitted and used to predict unknown values, it is important that an accuracy assessment is executed, and there are various ways that this can be achieved. The following sections describe some of the alternatives.

Cross-validation

A popular method of assessing accuracy that requires no independent data set is known as cross-validation. This involves fitting a model to all available data and then predicting each value in turn using all other data (that is, omitting the value to be predicted). The advantage of this approach is that all available data are used in model fitting (training). The main disadvantage is that the assessment is biased in favour of the model. That is, cross-validation may predict too high an accuracy because there is an inherent circularity in using the same data to fit and test the model.

Independent data for accuracy assessment

An alternative, and far preferable (if it can be afforded), approach is to use an independent data set (i.e. one not used in model fitting) to assess accuracy. In general terms, this data set should have some important properties. For example, the data should be representative of either the data to which the model was fitted (to provide a fair test of the model) or the data that actually need to be predicted (to assess the prediction). For continuous variables, given an independent testing data set, the full error cdf can be fitted and the parameters of that distribution estimated. Also, summary statistics such as the mean error (bias) and RMSE (accuracy) can be estimated readily. Further, the ‘known’ values may be plotted against the predicted values and the linear model used to estimate the correlation coefficient and other summaries of the bivariate distribution. The correlation coefficient, in this context, measures the association (i.e. precision)

whereis the covariance between y and z defined as

and sy and Sy are the standard deviations of y and y.

For categorical data, the accuracy assessment is based usually on a confusion matrix (or contingency table) from which a variety of summary statistics may be derived. These include the overall accuracy, the users’ and producers’ accuracies and the kappa coefficient, which attempts to compensate for chance agreement (Con-galton, 1991; Janssen and van der Wel, 1994).

Spatially distributed error

An accuracy assessment based on an independent data set may provide a spatially distributed set of errors (i.e. an error for every location that is predicted and for which independent testing data are available). These errors can be analysed statistically without the locational information. However, increasingly researchers are interested in the spatial information associated with error. For example, spatially, one might be interested in the local pattern of over- or under-prediction: the map of errors might highlight areas of over-prediction (positive errors) and under-prediction (negative errors). It has been found that in many cases such spatially distributed errors (or differences) are spatially autocorrelated (e.g. Fisher, 1998). That is, errors that are proximate in space are more likely to take similar values than errors that are mutually distant. In many cases, the investigator will be interested in spatial autocorrelation (e.g. the autocorrelation function could be estimated). Spatially autocorrelated error, which implies local bias, has important implications for spatial analysis.

Repeated measurement

Often, the objective is not to measure the accuracy of prediction, but rather to assess the precision associated with a given measurement process. A valid question is ‘how might one predict the errorgiven onlyOne possible solution is to measure repeatedly at the same locationwith the mean of the set of values predicting the true value, and the distribution of values conveying information on the magnitude of the likely error. For a single locationa sample of i = 1, 2, …, n = 100 valuescould be obtained. For example, suppose the objective was to quantify the precision in measurements of red reflectance from a heathland canopy made using a spectroradiometer (Figure 1.4). Repeated measurement at the same location would provide information on the spread of values around the prediction of the mean and, thereby, the variance associated with measurement.

The remainder of this topic is devoted to providing a gentle introduction to several important issues that are investigated in some depth within this topic.

Further Issues I: Spatial Resolution

Spatial resolution is a fundamental property of the sampling framework for both remote sensing and geographical information science. It provides a limit to the scale (or spatial frequency, in Fourier terms) of spatial variation that is detectable.

Figure 1.4 Repeated measurement of a heathland canopy (z) at a single locationusing a Spectron spectroradiometer.

It is the interplay between the scale(s) of spatial variation in the property of interest and the spatial resolution that determines the spatial nature of the variable observed. Importantly, all data (whether a remotely sensed image or data in a GIS) are a function of two things: reality and the sampling framework.One of the most important parameters of the sampling framework (amongst the sampling scheme, the sample size, sampling density) is the support. The support is the size, geometry and orientation of the space on which each observation or prediction is made. The support is a first-order property since it relates to individual observations. The spatial resolution, on the other hand, is second order because it relates to an ensemble of observations.

Scaling-up and scaling-down

The above link between spatial resolution and observed spatial variation makes the comparison of data obtained with different spatial resolutions a major problem for geographical information science. Before sensible comparison can be made it is important to ensure that the data are represented with the same sampling framework (e.g. two co-located raster grids with equal pixel size). In remote sensing, such comparison is often necessary to relate ground data (made typically with a small support) to image pixels that are relatively large (e.g. support of 30 m by 30m for a Landsat Thematic Mapper (TM)). The question is ‘how should the ground data be ”scaled-up” to match the support of the image pixels?’. In a GIS, where several variables may need to be compared (e.g. overlay for habitat suitability analysis) the problem may be compounded by a lack of information on the level of generalization in each variable (or data layer).

Much of the literature related to scaling-up and scaling-down actually relates to spatial resolution. The topic by Dungan describes the problems associated with scaling variables. In particular, where (i) non-linear transforms of variables are to be made along with (ii) a change of spatial resolution, the order in which the two operations (i.e. non-linear transform and spatial averaging) are undertaken will affect the final prediction. The two options lead to different results. Interestingly, there is not much guidance on what is the most appropriate order for the two operations (for some advice, see Bierkens et al., 2000).

Spatial resolution and classification accuracy

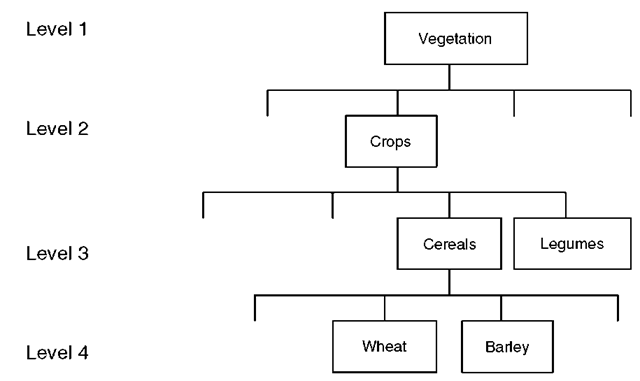
A reported, but surprising, phenomenon is that classification accuracy is often inversely related to spatial resolution (Townshend, 1981). Thus, a decrease in pixel size can result in a decrease in classification accuracy. However, there are two important points that mitigate against this result. The first is that the relation holds only for (i) a given level of spatial generalization and (ii) a given level of generalization in the possible hierarchical classification scheme (see Figure 1.5). Thus, the classification of patches within an agricultural field of barley into bare soil (which are in fact bare soil) will be regarded as misclassification if the investigator wishes the whole field to be classified as barley. This is a direct result of the level of spatial generalization. Further, if bare soil is not one of the land cover classes to be predicted then misclassification may again occur (as a result of, arguably, too general a classification scheme; see Figure 1.5).

Figure 1.5 Different levels of generalization in a classification hierarchy. Given a classification scheme at level 4, the separation of a field of barley into barley and bare soil may result in misclassification either (i) because the investigator wishes the whole field to be classified as barley or (ii) because the classification scheme does not permit it (e.g. there is no bare soil class)

The second, and more fundamental, point is that accuracy is only at most half of the picture. Of greater importance is information. As spatial resolution increases (pixels become smaller), so the amount of spatial variation, and thereby, the amount of information revealed increases.Thus, to compare the accuracy of classification for different spatial resolutions without reference to their information content amounts to an unfair comparison. As an example, consider the classification of land cover (into classes such as asphalt, grassland and woodland) based on Landsat TM imagery (pixels of 30m by 30m) and IKONOS multispectral imagery (pixels of 4m by 4m). The classification accuracy might be greater for the Landsat TM imagery, but only on a per-30m pixel basis. What if the information required was a map of the locations of small buildings (around 10 m by 10 m) within the region? The Landsat TM imagery would completely fail to provide this level of information. What is the point of predicting more accurately if the spatial information provided is inadequate?

For example, these are the sort of issues that providers of remotely sensed information have to face. The topic by Smith and Fuller describes the problems surrounding defining the spatial resolution of the Land Cover Map of Great Britain 2000 and, in particular, the decision to map using parcel-based units rather than pixel units. The topic by Manslow and Nixon goes beyond issues of spatial resolution by considering the effects of the point-spread function of the sensor on land cover classification. Further, Jakomulska and Radomski describe the issues involved in choosing an appropriate window size for texture-based classification of land cover using remote sensing.

Further Issues II: Soft Classification

It has been assumed so far that remote sensing classification is ‘hard’ in the sense that each pixel is allocated to a single class (e.g. woodland). However, in most circumstances soft classification, in which pixels are allocated to many classes in proportion to the area of the pixel that each class represents, provides a more informative, and potentially more accurate, alternative. For example, where the spatial resolution is coarse relative to the spatial frequency of land cover, many pixels will represent more than one land cover class (referred to as mixed pixels). It makes little sense to allocate a mixed pixel to a single class. Even where the spatial resolution is fine relative to the spatial frequency of land cover, soft classification may be more informative than hard classification at the boundaries between land cover objects (where mixed pixels inevitably occur). Thus, since the mid-1980s (Adams et al., 1985), soft classification has seen increasingly widespread use.

Despite the clear advantages of soft classification of land cover (land cover proportions are predicted), usually no information is provided about where within each pixel the land cover actually exists. That is, land cover is not mapped within each pixel.These, and related techniques, allow the prediction of land cover (and potentially other variables) at a finer spatial resolution than that of the original data.

Further Issues III: Conditional Simulation

Warr et al.use conditional simulation to solve the problem of predicting soil horizon lateral extent. In this section, conditional simulation is introduced as a valuable tool for spatial uncertainty assessment.

A problem with kriging is that the predicted variable is likely to be smoothed in relation to the original sample data. That is, some of the variance in the original variable may have been lost through kriging. Most importantly, the variogram of the predictions is likely to be different to that of the original variable meaning that the kriged predictions (map) could not exist in reality (‘not a possible reality’) (Journel, 1996). A solution is provided by conditional simulation which seeks to predict unknown values while maintaining, in the predicted variable, the original variogram (seeDungan, 1998, for a comparison of kriging and conditional simulation in remote sensing). A simple technique for achieving a conditional simulation is known as sequential Gaussian simulation (sGs). Given the multi-Gaussian case (i.e. that a multi-Gaussian model is sufficiently appropriate for the data) the kriging variance is sufficient (note that kriging ensures unbiasedness) to characterize fully the conditional cdf (ccdf) of the prediction. All nodes to be simulated are visited in (usually random) order. The ccdf of any location to be simulated is conditional on all data and previously simulated nodes such that any draw from the generated set of ccdfs will reproduce the original variogram.

Interestingly, while the variogram (i.e. the spatial character) is reproduced, the prediction variance of any simulation is double that for kriging. Thus, conditional simulation represents the decision to put greater emphasis (and less uncertainty) on the reproduction of spatial character and less emphasis (and greater uncertainty) on prediction.

Further Issues IV: Non-stationarity

Lloyd  provides an example of a non-stationary modelling approach in geostatistics. Many of the models that are applied in remote sensing and geographical information science are stationary in a spatial sense. Stationarity means that a single model is fitted to all data and is applied equally over the whole geographic space of interest. For example, to predict LAI from NDVI a regression model might be fitted to coincident data (i.e. where both variables are known) and applied to predict LAI for pixels where only NDVI is known. The regression model and its coefficients are constant across space meaning that the model is stationary. The same is true of geostatistics where a variogram is estimated from all available data and the single fitted model (McBratney and Webster, 1986) used to predict unobserved locations.

An interesting and potentially efficient alternative is to allow the parameters of the model to vary with space (non-stationary approach). Such non-stationary modelling has the potential for greater prediction precision because the model is more tuned to local circumstances, although clearly a greater number of data (and parameters) is required to allow reliable local fitting. In some cases, for example, geographically weighted regression (Fotheringham et al., 2000), the spatial distribution of the estimated parameters is as much the interest as the predicted variable.

Conclusions

Uncertainty is a complex and multi-faceted issue that is at the core of (spatial) statistics, is of widely recognized importance in geographical information science and is of increasing importance in remote sensing. It is fundamentally important to agree terms and their definitions to facilitate the communication of desired meanings. While it is impossibly difficult to hold constant any language, particularly one in rapidly changing fields such as remote sensing and geographical information science, we believe that it is an important and valid objective that the meanings of terms should be shared by all at any one point in time. The view taken in this topic is that the remote sensing and geographical information science communities should, where relevant, adopt the terminology used within statistics (e.g. Cressie, 1991), and otherwise should adopt terms that convey clearly the author’s meaning.