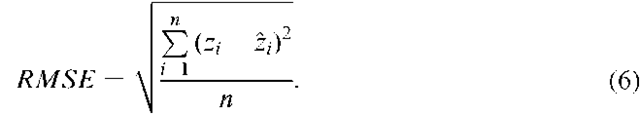Introduction
Uncertainty has been an important topic in geographical information science for over a decade (e.g. Goodchild and Gopal, 1989; Veregin, 1996; Kiiveri, 1997; Heu-velink, 1998; Zhang and Goodchild, 2002). This focus has led researchers to recommend over many years that the spatial output of a geographical information system (GIS) should be (at least) twofold: (i) a map of the variable of interest and (ii) some assessment of uncertainty in that map. Uncertainty has also been the subject of much research in remote sensing,with the main focus of such work being the assessment (and increase) of prediction or classification accuracy. However, uncertainty in remote sensing seems to have been a less explicit focus of research effort than uncertainty in GIS, with perhaps fewer calls for the production of maps depicting uncertainty.
This topic aims to (i) discuss the nature of uncertainty; its interpretation, assessment and implications, (ii) assemble a range of up-to-date research on uncertainty in remote sensing and geographical information science to show the current status of the field and (iii) indicate future directions for research. We seek, in this introductory topic, to define uncertainty and related terms. Such early definition of terms should help to (i) provide a common platform upon which each individual topic can build, thus, promoting coherence and (ii) avoid duplication of basic material, thus, promoting efficiency in this topic. We have done this also in the hope that others will adopt and use the definitions provided here to avoid confusion in publications in the future. We start with uncertainty itself.
Uncertainty arises from many sources ranging from ignorance (e.g. in understanding), through measurement to prediction. The Oxford English Dictionary gives the following definition of the word uncertain: ‘not known or not knowing certainly; not to be depended on; changeable’. Uncertainty (the noun) is, thus, a general concept and one that actually conveys little information. For example, if someone is uncertain, we know that they are not 100% sure, but we do not know more than that, for example, how uncertain they are or should be. If uncertainty is our general interest then clearly we shall need a vocabulary that provides greater information and meaning, and facilitates greater communication of that information. The vocabulary that we use in this topic involves clearly defined terms such as error, accuracy, bias and precision. Before defining such terms, two distinctions need to be made.
First, and paradoxically, to be uncertain one has to know something (Hoffman-Riem and Wynne, 2002). It is impossible to ascribe an uncertainty to something of which you are completely ignorant. This interesting paradox is explored by Curran in the Preface to this topic. Essentially, it is possible to distinguish that which is known (and to which an uncertainty can be ascribed) and that which is simply not known. In this topic, we deal with uncertainty and, therefore, that which is known (but not perfectly).
Second, dealing solely with that which is known, it is possible to divide uncertainty into ambiguity and vagueness (Klir and Folger, 1988). Ambiguity is the uncertainty associated with crisp sets. For example, in remote sensing, land cover is often mapped using hard classification (in which each pixel in an image is allocated to one of several classes). Each hard allocation is made with some ambiguity. This ambiguity is most often (and most usefully) expressed as a probability. Vagueness relates to sets that are not crisp, but rather are fuzzy or rough. For example, in remote sensing, land cover often varies continuously from place to place (e.g. ecotones, transition zones). In these circumstances, the classes should be defined as fuzzy, not crisp.
Error
An error![]() at location :
at location :![]() may be defined as the difference between the true value
may be defined as the difference between the true value ![]() and the prediction
and the prediction![]()
such that
Thus, errors relate to individual measured or predicted values (equations 1 and 2) and are essentially data-based. There is no statistical model involved. Thus, if we measure the soil pH at a point in two-dimensional space and obtain a value![]() of 5.6, where the true value
of 5.6, where the true value![]() is 5.62, the error
is 5.62, the error![]() is – 0.02.
is – 0.02.
Further, error has a very different meaning to uncertainty. In the example above, consider that both the predicted value (5.6) and the error (-0.02) are known perfectly. Then, an error exists, but there is no uncertainty. Uncertainty relates to what is ‘not known or not known certainly’. Thus, uncertainty is associated with (statistical) inference and, in particular, (statistical) prediction. Such statistical prediction is most often of the unknown true value, but it can equally be of the unknown error. Attention is now turned to three properties that do relate information on uncertainty: accuracy, bias and precision.
Accuracy, Bias and Precision
Accuracy may be defined in terms of two further terms: bias and precision (Figure 1.1). Accuracy, bias and precision are frequently misused terms. For example, researchers often use precision to mean accuracy and vice versa. Therefore, it is important to define these terms clearly. Let us, first, deal with bias and precision, before discussing accuracy.
Bias
Unlike error, bias is model-based in that it depends on a statistical model fitted to an ensemble of data values. Bias is most often predicted by the mean error, perhaps the simplest measure of agreement between a set of known values![]() and a set of predicted values
and a set of predicted values![]()
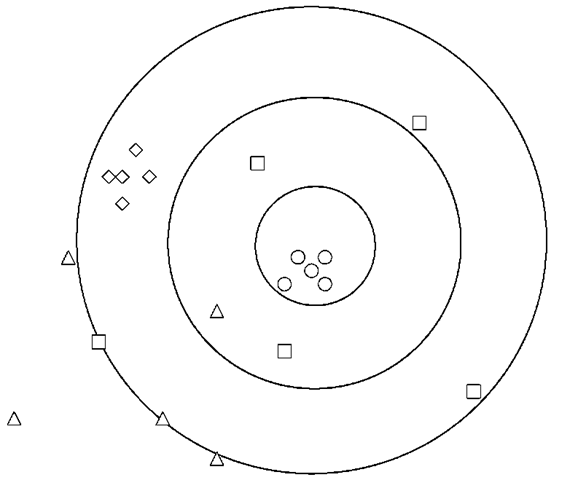
Figure 1.1 Bull’s eye target, represented by the set of concentric rings, with four sets of predictions, only one of which is accurate: (triangles) biased and imprecise, therefore, inaccurate; (squares) unbiased but imprecise, therefore, inaccurate; (diamonds) biased but precise, therefore, inaccurate; (circles) unbiased and precise, therefore, accurate.
Thus, bias is an expectation of over- or under-prediction based on some statistical model. The larger the (systematic) errors, the greater the bias.
Take a single measured value with a given error (equation 2). Suppose that the error is + 0.1 units. True, the measurement has over-predicted the true value. However, this does not imply bias: nor can bias be inferred from a single over-prediction. In simple terms, bias is what we might expect for a long run of measurements, or in the long term. Therefore, bias is a statistical expectation and to predict it, generally, we need an ensemble of values. If for a large sample the true value was consistently over-predicted we could infer that the measurement process was biased. Such inference is based on a statistical model.
Precision
Like bias, precision is model-based in that it depends on a statistical model fitted to an ensemble of values. Precision is most often predicted using some measure of the spread of errors around the mean error, for example, the standard deviation of the error, often termed the prediction error (where the prediction error is the square root of the prediction variance).
The standard deviation of the error can be predicted directly from the errors themselves if they are known
Thus, (im)precision is an expectation of the spread of errors. The smaller the (random) errors, the greater the precision. Such statistical inference is, again, model-based.
Accuracy
Accuracy is the sum of unbias (i.e. the opposite of bias) and precision:
Accuracy = Unbias + Precision (5)
This simple equation defining accuracy in terms of unbias and precision is fundamentally important in research into uncertainty.
Where an independent data set is used to assess uncertainty, accuracy may be predicted directly. In particular, the root mean square error (RMSE) which is sensitive to both systematic and random errors, can be used to predict accuracy
Accuracy, like bias and precision, depends on a statistical model. It is an expectation of the overall error.
It is important to distinguish between error and accuracy. Essentially, error relates to a single value and is data-based. Accuracy relates to the average (and, thereby, statistical expectation) of an ensemble of values: it is model-based. An actual observed error depends on no such underlying model. This distinction between model and data is fundamental to statistical analysis.
Model-based Prediction and Estimation
In this topic, and more generally in the literature relating to remote sensing and geographical information science, it is acknowledged that many authors use both estimation and prediction in relation to variables. However, in this topic, a distinction is made between the terms prediction and estimation. Prediction is used in relation to variables and estimation is used in relation to parameters. This is the scheme adopted by most statisticians and we shall adopt it here in the hope of promoting consistency in the use of terms.
Variables and parameters
Variables are simply measured or predicted properties such as leaf area index (LAI) and the normalized difference vegetation index (NDVI). Parameters are either constants (in a classical statistical framework) or vary (in a Bayesian framework), but in both cases define models. For example, two parameters in a simple regression model are the slope, fi, and intercept, a. In the classical framework, once a regression model is fitted to data, a and b, which estimate a and fl, are fixed and are referred to as model coefficients (i.e. estimated parameters). However, it is possible to treat parameters as varying. For example, within a Bayesian framework, parameters vary and their statistical distributions (i.e. their cumulative distribution functions, cdfs) are estimated. Thus, in the Bayesian framework, the distinction between estimation (of parameters) and prediction (of variables) disappears.
It is very difficult to achieve standardization on the use of the terms prediction and estimation. For example, authors often use estimate in place of predict. Such interchange of terms has been tolerated in this topic.
Prediction variance
Much effort has been directed at designing techniques for predicting efficiently, that is, with the greatest possible accuracy (unbiased prediction with minimum prediction variance). An equally large effort has been directed at predicting the prediction variance and other characteristics of the error cdf. Let us concentrate on the prediction of continuous variables. In particular, consider the prediction of the mean of some variable, to illustrate the basic concept of prediction variance.
Given a sample![]() for all i = 1, 2, 3, …, n of some variable z, the unknown mean ^ may be predicted using
for all i = 1, 2, 3, …, n of some variable z, the unknown mean ^ may be predicted using
The above model (equation 7) has been fitted to the available sample data, and the model used to predict the unknown mean.
From central limit theorem, for large sample size n the conditional cdf (i.e. the distribution of the error) should be approximately Gaussian (or normal) (see Figure 1.2) meaning that it is possible to predict the prediction error (and, therefore, imprecision) using the standard error, SE
Figure 1.2 Schematic representation of probability density function for prediction of the mean ^, with given standard error (SE)
where,
where, s is the standard deviation of the variable z and n is the number of data used to predict, in this case, the mean value (Figure 1.2). The prediction variance is simply the square of the standard error. As stated above, the standard error, and the prediction variance, are measures of precision. More strictly, in statistical terms, precision may be defined as the inverse of the prediction variance, although the term precision is more often used (and is used in this topic) less formally.
For a Gaussian model (i.e. a normal distribution), the mean and variance are the only two parameters. Therefore, given:
1. unbiasedness (i.e. the predicted mean tends towards the true mean as the sample size increases, such that the error can be assumed to be random) and
2. that the conditional cdf (i.e. the error distribution) is known to be Gaussian (e.g. via central limit theorem above)
then
3. the prediction variance (equivalent to the square of the standard error) is sufficient to predict the full distribution of the error.
For most statistical analyses, it is this error distribution (i.e. the full conditional cdf) that is the focus of attention.
It is useful to note that generally most statistical models can be used to infer precision, but not bias (and, therefore, not accuracy). For the example above involving predicting the mean, the SE conveys information only on precision. Nothing can be said about bias (or, therefore, accuracy) because we do not have any information by which to judge the predicted mean relative to the true mean (we can only look at the spread of values relative to the predicted mean). Statistical models are often constructed for unbiased prediction, meaning that the prediction error (or its square, the prediction variance), which measures imprecision (not bias), is sufficient to assess accuracy.
The example above involving predicting the regional mean can be extended to other standard statistical predictors. For example, linear regression (prediction of continuous variables) and maximum likelihood classification, MLC (prediction of categorical variables) are now common in remote sensing and geographical information science (Thomas et al., 1987; Tso and Mather, 2001). In both cases (i.e. regression or classification), the objective is prediction (of a continuous or categorical variable), but the model can be used to predict also the prediction error. The model must, first, be fitted to ‘training’ data. In regression, for example, the regression model is fitted to the scatterplot of the predicted variable y on the explanatory variable z (or more generally, z) in the sense that the sum of the squared differences between the line and the data (in the y-axis direction) is minimized (the least-squares regression estimator). For MLC, the multivariate Gaussian distribution is fitted to clusters of pixels representing each class in spectral feature space. Once the model has been fitted it may be used to predict unknown values given z (simple regression) or unknown classes given the multispectral values z (classification). However, the (Gaussian) model may be used (in both cases) to predict the prediction error. As with the SE, the prediction error is based on the variance in the original data that the models are fitted to.
There is not space here to elaborate further on standard statistical predictors. However, several of the topics in this topic deal with the geostatistical analysis of spatial data.Therefore, a brief introduction to geostatistical prediction is provided here for the reader who may be unfamiliar with the field.
Spatial prediction
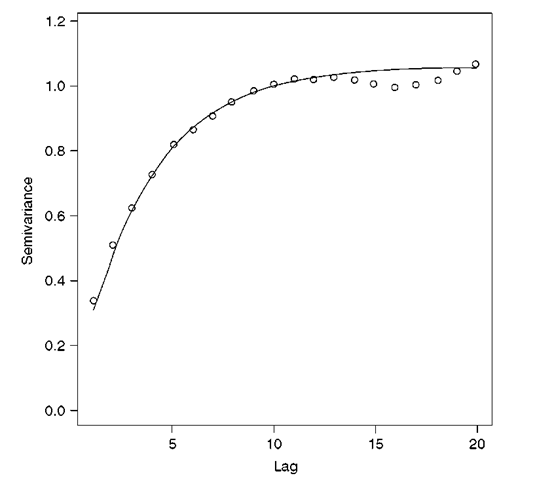
In geostatistics, the variogram is a central tool. Generally, the experimental vario-gram is predicted from sample data and a continuous mathematical model is fitted to it (Figure 1.3). This variogram model can then be used in the geostatistical technique for spatial prediction known as kriging (i.e. best linear unbiased prediction, BLUP). The variogram can, alternatively, be used in conditional simulation (Journel, 1996) or for a range of related objectives (e.g. optimal sampling design, van Groenigen et al., 1997; van Groenigen and Stein, 1998; van Groenigen, 1999).
Kriging is often used within a GIS framework to predict unknown values spatially from sample data; that is, to interpolate. Kriging has several important properties that distinguish it from other interpolators such as inverse distance weighting. In particular, since kriging is a least-squares regression-type predictor (Goovaerts, 1997; Deutsch and Journel, 1998; Chiles and Delfiner, 1999), it is able to predict with minimum prediction variance (referred to as kriging variance). Kriging predicts this kriging variance as a byproduct of the least-squares fitting (i.e. the regression). The kriging variance for a given predicted value, therefore, plays the same role as the square of the standard error for the predicted mean of a sample. However, the kriging variance is predicted for all locations (usually constituting a map). Thus, kriging is able to provide both (i) a map of the predicted values and (ii) a map of prediction variance: exactly what is required by users of GIS. A caveat is that the prediction variance is only minimum for the selected linear model (i.e. it is model-based).
A problem with the kriging variance is that it depends only on the variogram and the spatial configuration of the sample in relation to the prediction: it is not dependent on real local data values. However, for situations where local spatial variation is similar from place to place, the kriging variance provides a valuable tool for optimizing sampling design (Burgess et al., 1981). For example, for a fixed variogram, the sample configuration can be optimized for a given criterion without actual sample or
Figure 1.3 Exponential variogram model (line) fitted to an experimental variogram (symbols). The experimental variogram was obtained from an unconditional simulation of a random function model parameterized with an exponential covariance. The estimated exponential model parameters are as follows: non-linear parameter, r-\, is 3.5 pixels; sill variance, c-\, is 1.06 units. The model was fitted without a nugget variance, c0
A note on confidence intervals
Knowledge of the standard error allows the researcher to make statements about the limits within which the true value is expected to lie. In particular, the true value is expected to lie within ± 1 SE with a 68% confidence, within ± 2 SE with a 95% confidence and within ± 3 SE with (approximately) a 99% confidence.
There has been a move within statistics in recent years away from the use of confidence intervals. This is partly because confidence intervals are chosen arbitrarily. The problem arises mostly in relation to statistical significance testing. For example, in the case of the simple t-test for a significant difference between the means of two data sets the result of the test (is there a significant difference?) depends entirely on the (essentially arbitrary) choice of confidence level. A confidence of 68% may lead to a significant difference whereas one of 95% may not. Statistical significance testing is increasingly being replaced by probability statements.