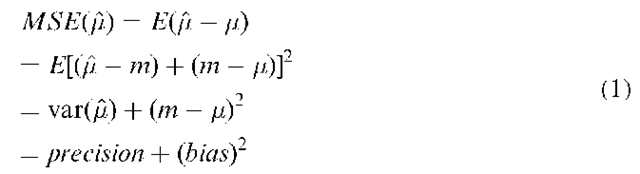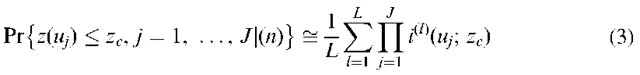Introduction
The topic of uncertainty has been receiving increasing attention in the geographical sciences (Kundzewicz, 1995; Mowrer and Congalton, 2000; Hunsaker et al., 2001; Odeh and McBratney, 2001). One might expect that an outgrowth of an increasingly mature science is a thorough quantification of uncertainty and its eventual reduction. However, if the scientific objective is to increase our understanding of the biogeo-physical world through remote sensing, does it necessarily make sense to strive for reduced uncertainty? After all, an argument can be made that, while a reduction in uncertainty may imply progress, an increase in uncertainty may also represent advancing understanding. When new observational evidence is acquired and is incompatible with the results of the currently accepted model, uncertainty has just increased. Uncertainty increases despite the informative nature of the new evidence. Nonetheless, more generally it is logical to expect that reduced uncertainty gauges success in applying models to data.
Descriptions of uncertainty are routine in statistical practice. Despite the fact that the analysis of remotely sensed data often relies on statistical methods, these descriptions have been often neglected in the presentation of remote sensing results. Perhaps part of the reason for this neglect is that describing uncertainty for geographical data is particularly difficult (Gahegan and Ehlers, 2000). Putting a prediction interval on the value at every spatial unit represented in a map generated from remotely sensed data has at least three challenges:
1. Spatial units are not generally independent, so statistical models that assume errors to be independent may be inadequate.
2. There are not enough reference data, measured using ground-based methods or other independent means, available to adequately test these intervals. Reference data for variables of interest to remote sensing analyses are often expensive and time-consuming to acquire and are not usually plentiful in a statistical sense.
3. It is a challenge to represent or visualize such spatially varying intervals or even distributions. In a non-spatial context, such intervals can be represented as stem-and-whisker plots – distributions can be represented as histograms. Representing uncertainty for a 2D map requires at least four or five dimensions and, therefore, becomes a problem in visualization.
In addition, uncertainty may change when one is talking about a single pixel or multiple pixels. That is, a confidence statement about the limited area represented by a single pixel may be different to a confidence statement about a larger area of which that pixel forms only a part.
The purpose of this topic is to advance a classification of the sources of uncertainty in the analysis of remote sensing data by incorporating statistical and geosta-tistical concepts.
What is Uncertainty?
The word uncertainty has resisted a narrow definition, possibly because unlike related words such as bias, precision, error and accuracy, the generic meaning of uncertainty deals with the subjective. That is, while two individuals may arrive at the same answer to a question, one individual may be more certain than the other about that answer. This subjectivity would suggest that uncertainty would escape rigorous scientific examination. However, given that measures of uncertainty are important for gauging progress, the most appropriate way to proceed is to use well-documented probability models, Bayesian or frequentist, that are agreed upon with some degree of consensus and that can be shown over time to be useful.
The definition of uncertainty to be used in this topic is the simple ‘quantitative statement about the probability of error’. A reasonable extrapolation of this definition is that accurately measured, estimated or predicted values will have small uncertainty; inaccurate measurements, estimates or predictions should be associated with large uncertainty. This explanation is not very helpful until the term accuracy is discussed further, because it turns out that there are two conflicting interpretations in the current literature of how accuracy relates to error.
Something that is accurate should lack error (Taylor and Kuyatt, 1994). Accuracy has traditionally been defined (Johnston, 1978) to mean more specifically that
1. on average, the error is insignificantly small – values are unbiased, and
2. the spread of those errors is also small – values are precise.
Cochran (1953) clearly stated the orthodox view in statistics about these two components of accuracy in parameter estimation theory. In his discussion of estimating the mean parameter, he states, ‘Because of the difficulty of ensuring that no unsuspected bias enters into estimates, we shall usually speak of the precision of an estimate rather than its accuracy. Accuracy refers to the size of the deviations from the true mean (u), whereas precision refers to the size of deviations from the mean (m) obtained by repeated application of the sampling procedure’ (Cochran, 1953, p. 15). Olea (1990, p. 2) also reflects this view, stating that, ‘Accuracy presumes precision, but the converse is not true’. Both Cochran and Olea mention mean square error (MSE) as a typical quantifier of accuracy:
where
is the estimate of the true value of the parameter
is distributed around the potentially biased m, where m is calculated from a sample of the population. By this reasoning, inaccurate values may, therefore, occur if they are biased though precise, unbiased and imprecise or, most obviously, biased and imprecise.
A contrasting definition has been used by others (e.g. Maling, 1989; Goovaerts, 1997; Mowrer and Congalton, 2000) who equate accuracy directly with unbiased-ness. This implies that a set of imprecise values, as long as it is unbiased, is declared accurate. This alternative interpretation of accuracy is rejected here because a definition of uncertainty that ignores imprecision or random error would not be terribly useful. Therefore, the probability of error incorporated into uncertainty bounds should represent both the random and systematic components of error.
Sources of Uncertainty
To explicate the sources of uncertainty in remote sensing analyses, consider that remotely sensed data are observations on a variable or, more often because of the multi-spectral nature of most sensors, multiple variables; the objective of analysis is to transform these variables to obtain new variables of interest. In equation form, this can be expressed as:
where z is a variable with values on some nominal, ordinal, interval or ratio scale; y is a vector of input variables; v is the spatial support of y and z; x and u are the spatial locations of y and z, respectively; f is a model and 0 is the vector of the parameters of this model. The variables yv(x) and zv(u) are both examples of the geographical datum defined by Gahegan (1996); they each have a value and a spatial extent. The geostatistical term ‘support’ is used here to refer to this spatial extent. Strictly, these variables also have a temporal extent and a time for which they are relevant. For simplicity, temporal aspects are neglected herein.
An important distinction (conventional in statistics) is made in equation (2) between variables, which here are a function of location, and parameters, which are not a function of location but a part of the model. The job of analysis is, therefore, to predict values of the variable z with support v at every location u using a model and its parameters.
An example of the application of equation (2) is the transformation of digital numbers (y = DN) to surface reflectance (z = p). In this case, f would be a non-linear function and parameters 0 might include atmospheric optical depth, total irradiance and the backscatter ratio if the region was flat and these were considered spatially constant. Another example would be the identification of a nominal land cover class at each pixel based on DN. The model in this case is a classification algorithm, whose parameters include the means and covariances of spectral classes. z may also be defined as a ‘fuzzy’ class.usually represented as a continuous variable ranging between 0 and 100% and predicted using any one of the fuzzy classification.Friedl et al. (2001) describe another family of examples, called ‘inversion techniques’ – the transformation of spectral variables into continuous variables related to vegetation structure or density. The models for these analyses have included empirically derived regression models where the shape of the regression is chosen from the data to be analysed, semi-empirical models where the shape of the regression model is chosen based on physical theory, or canopy reflectance models.
Putting analyses into the framework of equation (2) implies a different perspective on uncertainty to that of Friedl et al. (2001, p. 269), who stated, ‘It is important to note that the errors introduced to maps produced by [...] remote sensing inversion techniques are of an entirely different nature and origin than thematic errors present in classification maps’. In equation (2), classification is placed into the same context as inversion techniques, where the probability of error is influenced by the spectral variables used in the process, the classification algorithm and the parameters selected in that algorithm.
The perspective adopted is similar to that of the ‘image chain approach’ described by Schott (1997). A complex analysis would be broken down by the image chain approach into a sequence of applications of simple models f, where the z variable from each step in the sequence would become a y variable in the next step. Expressing remote sensing analysis using this framework makes it clear that uncertainty can arise about input variables, their locations and spatial supports, the model and parameters of the model (Table 3.1). Each of these sources of uncertainty is discussed below.
Table 3.1 Sources of uncertainty in remote sensing analysis. Refer to equation (2) for definition of symbols
|
Symbol(s) |
Source |
 |
positional |
 |
support |
 |
parametric |
 |
structural |
 |
variable |
Uncertainty about parameters
Parametric uncertainty is perhaps the most familiar type because of the emphasis on parameter estimation in basic statistics courses. Methods to estimate parameters usually incorporate unbiasedness criteria and maximum precision (the least squares criterion). Characterizing parametric uncertainty is typically accomplished using training data for the input variables. Statements about parametric uncertainty assume that the model associated with the parameters is known with certainty.
In the above example about the conversion of DN to reflectance, a decision may be made to treat optical depth as a parameter. Uncertainty about the value of this optical depth parameter might then be informed by the variation among dark targets in relevant imagery. On the other hand, if optical depth is treated as a variable and so is a y rather than a 9, it is expected to vary spatially. In this case, the variation among dark targets would pertain to both the actual values of optical depth and its uncertainty.
It is an easier problem to estimate parameters than to predict variables; in general, there is less uncertainty about them than about variables. This is because parameters, by definition, are constant throughout the image domain to which the model is applied. Therefore, all of the data available for training or calibrating the model can be used to obtain the expected value and its distribution for the parameter. The relative certainty of parameters can be seen in the familiar contrast (Draper and Smith, 1998) between confidence intervals for a mean and prediction intervals for unmeasured values. Confidence intervals are in general narrower than prediction intervals.
Uncertainty about models
Less often acknowledged, but always present, is uncertainty about the form or structure of the model used to transform the input variables to the desired output variables. Draper (1995) calls this structural uncertainty. Structural uncertainty comes from the fact that several models are potentially useful to describe the phenomenon being studied. For instance, a nearest mean and a maximum likelihood algorithm are each based on reasonable models for a classification problem. If a set of models are considered, each of which gives different results, uncertainty is attached to the fact that the most accurate model is unknown. The type of error likely to occur is bias error. Because it is time-consuming and labour intensive to accomplish many analyses, usually it has not been profitable for multiple models to be tried. If they are tried, a common occurrence is that one preferred analysis is chosen based on the results on a very small sample and other analyses are discarded.
Datcu et al. (1998) deal explicitly with the ideas of model fitting, where parametric uncertainty is relevant, and model selection. They suggest that the choice of a model may be one of the biggest sources of uncertainty. More generally, the precise path of analysis contains many decision points. Alternatives at any one of these decision points may generate uncertainty. For instance, results of thematic classifications may vary greatly when independent analysts construct them (Hansen and Reed, 2000). An influential study in geostatistics (Englund, 1990) showed that the spread of outcomes from alternative analysis paths can result in large uncertainty, with bias as the major concern.
Uncertainty about support
Spatial support is a concept from geostatistics that refers to the area over which a variable is measured or predicted.For remotely sensed data, the support can be considered that area covered by the effective resolution element (ERE), a function of the instantaneous field of view, flight variables such as altitude, velocity and attitude and atmospheric effects (Forshaw et al., 1983). The variables for which data are available, the y, have a spatial support v defined by this ERE. It may or may not be the aim to predict the z variable on the same spatial support.
The support of remotely sensed data is never known precisely. There are no real boundaries of a pixel and the value represented at a pixel is not a strict spatial average of that unknown area (Fisher, 1997). The point spread function used to model the sensor response describes the y value as an unequally weighted integral of its spatial extent. Yet more often than not, approximations to the support are made using the grid cell size reported in image metadata. Efforts have, therefore, been made to increase the precision with which this value is known (e.g. Schowengerdt et al., 1985).
Uncertainty about position
Uncertainty about x and u, the locations of the data values, is routinely addressed in image analysis. The ‘raw’ images delivered for analysis by a data provider incorporate positional errors because of the process of converting a sensor’s responses to a raster data structure. This delivered raster is usually registered or georectified prior to the application of any form of equation (2). Registration can be accomplished using different approaches; those which use only ground control points (GCPs) that can also be identified in the image or those which model the scene and its observation geometry. Regardless of the approach used, uncertainty metrics can be usefully derived from a set of numerous ‘test’ points, or what Schowengerdt (1997) calls ground points (GPs other than the GCPs used to train or calibrate the registration process). Customarily, only a root-mean-square error on GPs is reported when it would be even more useful to report the distribution of errors – unsuspected bias might sometimes be uncovered (Lewis and Hutchinson, 2000).
Numerous studies have examined the relationships between values of remotely sensed spectral variables (say, y(x)) at locations within images and ground-based observations of variables (say, z(u)) such as temperature, vegetation amount and pigment concentration. A way to think of this type of study is to regard it as a search for a model f that fits the observed data. Because precise co-location of the remotely sensed and ground-measured variables is important in this type of study, a common practice in these studies is to use an average of values from a 2 x 2, 3 x 3 or 4 x 4 pixel window area surrounding the estimated position of the ground-based observation to represent the spectral variable. The average is taken in an attempt to reduce the positional uncertainty of u. This practice essentially increases the support of the spectral variables y. The aggregation effect will act to reduce variance of the y and the statistics used as criteria for model-fitting will differ from what they would be if y and z were on the same support.
Uncertainty about variables
Uncertainty about the input variables y exists as a function of the measurement process (i.e. measurement error) or whatever transformation came prior to the current one in the image chain. In addition, parametric, structural, support and positional uncertainty lead to uncertainty about variables predicted by the model. This can be understood as an error or uncertainty propagation problem. Techniques exist to handle some aspects of the propagation problem (Heuvelink and Burrough, 1993), but a fuller treatment of all five aspects has yet to be formulated (Gahegan and Ehlers, 2000).
The Spatial Support Factor
Why make support explicit in equation (2)? This way of characterizing analyses implies that a variable, for example the normalized difference vegetation index (NDVI), defined on a specific support, say 900 m2, is fundamentally different than the NDVI defined at another support, say 6400 m2. Framing variables this way makes it evident that uncertainty is influenced by the size of v. Because of the aggregation effect, the values from a set of large pixels covering a region will have smaller variance than the values from a set of small pixels covering the same region. And since the sample variance is used as an estimate of population variance in formulas for confidence and prediction intervals, variable uncertainty should be smaller (or precision should be greater) for large rather than small pixels, all other factors remaining equal. Of course, all other factors rarely remain equal!
Another reason to make the support explicit is to think about the uncertainty that may arise when the same model f is used in analyses with different variable supports v. This situation has often been met in environmental modelling with geographic data derived from remote sensing. Take the case of a z variable with support v that is to be predicted using the modelf. Further, specify that this model is non-linear, such as a ratio transform, exponential or higher order polynomial. If the model is not changed, but v is increased or decreased, this will affect the values of z that are predicted and add uncertainty about model results, most likely in the form of bias. Several investigators using deterministic models of ecosystem processes that require remotely sensed inputs have studied this phenomenon. Over a range of input spatial unit sizes that differed by up to over 100 fold (from 1 km to 1°), Pierce and Running (1995) reported that estimates of net primary production (NPP) increased up to 30% using the BIOME-BGC model and remotely sensed leaf area index values. Lammers et al. (1997), using a related model (RHESSys), also reported significantly larger values of photosynthesis and evapotranspiration when moving from smaller grid cells to larger (comparing 100 m to 1 km) grid cells. Over an input pixel size range of 25 m to 1 km, Turner et al. (2000) found a decrease in NPP of 12% and an increase in total biomass estimates of 30% using a ‘measure and multiply’ method. Looking at a much smaller range of pixel sizes (30 m to 80 m, less than three-fold), Kyriakidis and Dungan (2001) found that aggregated input data reduced NPP estimates slightly using the CASA (Potter et al. 1993) model. While all of these studies identified bias in model results, they did not find the same direction or magnitude of the effect. Heuvelink and Pebesma (1999) provide an excellent summary of a similar situation in the application of pedometric transforms.
Multiple Pixel Uncertainty
To this point, only uncertainty at an individual location u for the variable z has been discussed. Many applications require predictions about multiple-pixel regions, and issues of uncertainty become more complicated in such circumstances. It stands to reason that uncertainty about attribute values at a single location is a different issue to that about an attribute value at a number of locations. It is because of this difference that geostatisticians have developed the concepts of local versus spatial uncertainty (Goovaerts, 1997). Local uncertainty considers one location at a time whereas spatial uncertainty considers contiguous locations jointly. Kyriakidis (2001) describes a method for estimating spatial uncertainty about the variable z at a set of J locations uy using L simulations of the conditional probability
where
is some threshold value, (n) are all the observed (reference) data,
is an indicator variable (see van der Meer, 1996), denotes the product and L is the number of simulations. This model has yet to be employed extensively in remote sensing.
Both parametric and model uncertainty can be considered global, at least (and sometimes at the most!) for the region to be analysed. There is, therefore, no need to make the multiple-pixel distinction for these two sources of uncertainty. Positional uncertainty, on the other hand, has a multiple-pixel aspect. For example, characterizing the uncertainty in the position of a linear feature (Jazouli et al., 1994) or an areal feature is more problematic than characterizing uncertainty about the locations of single pixels.
An aspect of uncertainty in remote sensing analysis that is not captured by viewing problems as forms of equation (2) is when the ultimate objective is to estimate the area covered by z equal to a value or range of values. Several investigators have turned their attention to this problem (e.g. Crapper, 1980; Dymond, 1992; Mayaux and Lambin, 1997; Hlavka and Dungan, 2002). As support changes, bias in area estimation is likely to change. The trend depends on the real spatial distribution of the feature whose area is being estimated and how the support of the remotely sensed data compares with this distribution. For example, Benjamin and Gaydos (1990) found that bias in estimating the area of roads decreased with supports ranging from approximately 1 to 3 m2 and then increased with supports ranging from approximately 3 to 6 m2. Area estimation is obviously a multiple-pixel problem.
Conclusion
This topic has presented a perspective that allows many sources of uncertainty to be identified and distinguished. It has highlighted two sources of uncertainty that have received little attention in the remote sensing literature: model (or structural) uncertainty and uncertainty about spatial support. The framework of equation (2) shows how uncertainty from all sources are inextricably linked. Quantifying parametric, structural, support and positional uncertainty are all intermediate goals toward understanding uncertainty about variables. It is the values of variables that represent the ultimate purpose of many remote sensing analyses.
Remotely sensed data are a special kind of geographical data, and as such share many properties. Sinton’s (1978) categorization of uncertainty for geographical data included value, spatial location, temporal location, consistency and completeness. This topic has discussed value and spatial location, but neglected temporal location. As for the fourth category, consistency, the premise of this topic is that the outcome of a remote sensing analysis can never be truly consistent in the sense that uncertainty will vary spatially. This ‘inconsistency’ is exacerbated by the data scarcity problem, since the number of reference data available relative to the size of the whole field being predicted is usually miniscule. However, analyses done with the same spatial supports on both sides of the equal sign in equation (2) should be more consistent than those with unequal supports. Finally, remotely sensed data sets are usually considered complete, at least for the region represented by the images at hand.
Further research, perhaps using Bayesian models (Datcu et al., 1998) that make support an explicit factor, should enhance methods of quantifying uncertainty. Doing so will increase the ability to identify the largest sources of uncertainty and help focus research efforts on these ‘weakest links’ in the image analysis chain.
