When looking in our world, it has three dimensions — up and down, left and right, back and forth. If you give a longitude, latitude, and an altitude, you can determine any location on Earth, for example.
A straight line in space: Vectors
Expanding on the idea of Cartesian geometry, you find that it’s possible to create a Cartesian grid in three dimensions as well as two, as shown in Figure 13-3. In such a grid, you can define an object called a vector, which has both a direction and a length. In 3-dimensional space, every vector is defined by three quantities.
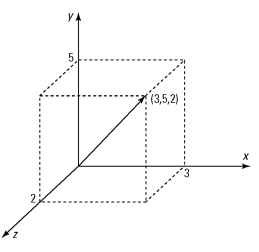
Figure 13-3:
It takes three numbers to define a vector (or location) in three dimensions.

Vectors can, of course, exist in one, two, or more than three dimensions. (Technically, you can even have a zero-dimensional vector, although it will always have zero length and no direction. Mathematicians call such a case “trivial.”)
Treating space as containing a series of straight lines is probably one of the most basic operations that can take place within a space. One early field of mathematics that focuses on the study of vectors is called linear algebra, which allows you to analyze vectors and things called vector spaces of any dimensionality. (More advanced mathematics can cover vectors in more detail and extend into nonlinear situations.)
One of the major steps of working with vector spaces is to find the basis for the vector space, a way of defining how many vectors you need to define any point in the entire vector space. For example, a 5-dimensional space has a basis of five vectors. One way to look at superstring theory is to realize that the directions a string can move can only be described with a basis of ten distinct vectors, so the theory describes a 10-dimensional vector space.
Twisting 2-dimensional space in three dimensions: The Mobius strip
In the classic topic Flatland, the main character is a square (literally — he has four sides of equal length) who gains the ability to experience three dimensions. Having access to three dimensions, you can perform actions on a 2-dimensional surface in ways that seem very counterintuitive. A 2-dimen-sional surface can actually be twisted in such a way that it has no beginning and no end!
The best known case of this is the Mobius strip, shown in Figure 13-4. The Mobius strip was created in 1858 by German mathematicians August Ferdinand Mobius and Johann Benedict Listing.
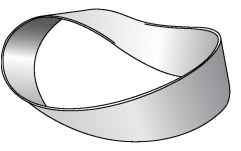
Figure 13-4:
A Mobius strip is twisted so it has only one continuous surface.
You can create your own Mobius strip by taking a strip of paper — kind of like a long topicmark — and giving it a half-twist. Then take the two ends of the strip of paper and tape them together. Place a pencil in the middle of the surface and draw a line along the length of the strip without taking your pencil off the paper.
A curious thing happens as you continue along. Eventually, without taking your pencil from the paper, the line is drawn on every part of the surface and eventually meets up with itself. There is no “back” of the Mobius strip, which somehow avoids the pencil line. You’ve drawn a line along the entire shape without lifting your pencil.
In mathematical terms (and real ones, given the result of the pencil experiment), the Mobius strip has only one surface. There is no “inside” and “outside” of the Mobius strip, the way there is on a bracelet. Even though the two shapes may look alike, they are mathematically very different entities.
The Mobius strip does, of course, have an end (or boundary) in terms of its width. In 1882, the German mathematician Felix Klein expanded on the Mobius strip idea to create a Klein bottle: a shape that has no inside or outside surface, but also has no boundaries in any direction. Take a look at Figure 13-5 to understand the Klein bottle. If you traveled along the “front” of the path (with the x’s), you’d eventually reach the “back” of that path (with the o’s).
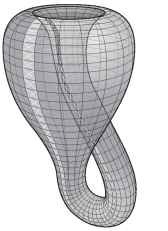
Figure 13-5:
A Klein bottle has no boundary (edge).

If you were an ant living on a Mobius strip, you could walk its length and eventually get back to where you started. Walking its width, you’d eventually run into the “edge of the world.” An ant living on a Klein bottle, however, could go in any direction and, if it walked long enough, eventually find itself back where it started. (Traveling along the o path eventually leads back to the x’s.) The
difference between walking on a Klein bottle and walking on a sphere is that the ant wouldn’t just walk along the outside of the Klein bottle, like it would on a sphere, but it would cover both surfaces, just like on the Mobius strip.
More twists in three dimensions: Non-Euclidean geometry
The fascination with strange warping of space in the 1800s was perhaps nowhere as clear as in the creation of non-Euclidean geometry, where mathematicians began to explore new types of geometry that weren’t based on the rules laid out 2,000 years earlier by Euclid. One version of non-Euclidean geometry is Riemannian geometry, but there are others, such as projective geometry.
The reason for the creation of non-Euclidean geometry is based in Euclid’s Elements itself, in his “fifth postulate,” which was much more complex than the first four postulates. The fifth postulate is sometimes called the parallel postulate and, though it’s worded fairly technically, one consequence is important for string theory’s purposes: A pair of parallel lines never intersects.
Well, that’s all well and good on a flat surface, but on a sphere, for example, two parallel lines can and do intersect. Lines of longitude — which are parallel to each other under Euclid’s definition — intersect at both the north and south poles. Lines of latitude, also parallel, don’t intersect at all. Mathematicians weren’t sure what a “straight line” on a circle even meant!
One of the greatest mathematicians of the 1800s was Carl Friedrich Gauss, who turned his attention to ideas about non-Euclidean geometry. (Some earlier thoughts on the matter had been kicked around over the years, such as those by Nikolai Lobachevsky and Janos Bolyai.) Gauss passed the majority of the work off to his former student, Bernhard Riemann. Riemann worked out how to perform geometry on a curved surface — a field of mathematics called Riemannian geometry. One consequence — that the angles of a triangle do not add up to 180 degrees — is depicted in Figure 13-6.
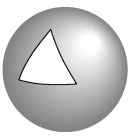
Figure 13-6:
Sometimes the angles of a triangle don’t measure up to 180 degrees.
The mathematics of artwork
Understanding and manipulating space is a key feature of artwork, which often attempts to reflect a 3-dimensional reality on a 2-dimen-sional surface. This is probably most notable in the work of Pablo Picasso and M. C. Escher, where space has been manipulated in such a way that the manipulation itself is part of the artistic message.
Most artists try to manipulate space so it’s not noticed. One of the most common examples of this is perspective, developed during the Renaissance, which involves creating an image that matches the way the eye perceives space and distance. Parallel railroad tracks appear to meet at the horizon, though they never meet in reality. On a 2-dimensional surface, the basis for the railroad tracks is a triangle that does, in fact, have a corner at the horizon line.
This is precisely the basis of the mathematical field of non-Euclidean geometry called projective geometry, where you take one 2-dimensional space and project it in a precise mathematical way onto a second surface. There is an exact 1-to-1 correspondence between the two spaces, even though they look completely different. The two images represent different mathematical ways of looking at the same physical space — one of them an infinite space and one a finite space.
When Albert Einstein developed general relativity as a theory about the geometry of space-time, it turned out that Riemannian geometry was exactly what he needed.
