We move through time every single day, and most of us don’t even think about how fascinating it is. Scientists who have thought about it have constantly run into trouble in figuring out exactly what time means because time is such an abstract concept. It’s something we’re intimately familiar with, but so familiar with that we almost never have to analyze it in a meaningful way.
Over the years, our view of time — both individually and from a scientific standpoint — has changed dramatically, from an intuition about the passage of events to a fundamental component of the mathematical geometry that describes the universe.
The arrow of time: A one-way ticket
Physicists refer to the one-way motion through time (into the future and never the past) using the phrase “arrow of time,” first used by Arthur Eddington (the guy who helped confirm general relativity) in his 1928 topic The Nature of the Physical World. The first note he makes is that “time’s arrow” points in one direction, as opposed to directions in space, where you can reorient as needed. He then points out three key ideas about the arrow of time:
Human consciousness inherently recognizes the direction of time.
Even without memory, the world only makes sense if the arrow of time points into the future.
In physics, the only place the direction of time shows up is in the behavior of a large number of particles, in the form of the second law of thermodynamics. (See the nearby sidebar, “Time asymmetries,” for a clarification of the exceptions to this.)
The conscious recognition of time is the first (and most significant) evidence that any of us has about the direction we travel in time. Our minds (along with the rest of us) “move” sequentially in one direction through time, and most definitely not in the other. The neural pathways form in our brain, which retains this record of events. In our minds, the past and future are distinctly different. The past is static and unchanging, but the future is fully undetermined (at least so far as our brain knows).
As Eddington pointed out, even if you didn’t retain any sort of memory, logic would dictate that the past must have happened before the future. This is probably true, although whether one could conceptualize of a universe in which time flowed from the future to the past is a question that’s open for debate.
Time asymmetries
Arthur Eddington’s third observation about the arrow of time indicates that physical laws actually ignore the direction of time, except for the second law of thermodynamics. What this means is that if you take the time t in any physics equation and replace it with a time -t, and then perform the calculations to describe what takes place, you’ll end up with a result that makes sense.
For gravity, electromagnetism, and the strong nuclear force, changing the sign on the time variable (called T-symmetry) allows the laws of physics to work perfectly well. In some special cases related to the weak nuclear force, this actually turns out not to be the case.
There is actually a larger type of symmetry, called CPT symmetry, which is always preserved. The C stands for charge-conjugation symmetry, which means that positive and negative charges switch. The P stands for parity symmetry, which involves basically replacing a particle for a complete mirror image — a particle that has been flipped
across all three space dimensions. (This CPT symmetry is a property of quantum theory in our four-dimensional space-time, so at present we are ignoring the other six dimensions proposed by string theory.)
The total CPT symmetry, it turns out, appears to be preserved in nature. (This is one of the few cases of unbroken symmetry in our universe.) In other words, an exact mirror image of our universe — one with all matter swapped for antimatter, reflected in all spatial directions, and traveling backward in time — would obey physical laws that are identical to those of our own universe in every conceivable way.
If CP symmetry is violated, then there must be a corresponding break in T-symmetry, so the total CPT symmetry is preserved. In fact, the handful of processes that violate T-symmetry are called CP violations (because the CP violation is easier to test than a violation in the time-reversal symmetry).
Finally, though, we reach the physics of the situation: the second law of thermodynamics. According to this law, as time progresses, no closed system (that is, a system that isn’t gaining energy from outside of the system) can lose entropy (disorder) as time progresses. In other words, as time goes on, it’s not possible for a closed system to become more orderly.
Intuitively, this is certainly the case. If you look at a house that’s been abandoned, it will grow disordered over time. For it to become more orderly, there has to be an introduction of work from outside the system. Someone has to mow the yard, clean the gutters, paint the walls, and so on. (This analogy isn’t perfect, because even the abandoned house gets energy and influence from outside — sunlight, animals, rainfall, and so on — but you get the idea.)
In physics, the arrow in time is the direction in which entropy (disorder) increases. It’s the direction of decay.

Oddly, these same ideas (the same in spirit, though not scientific) date all the way back to St. Augustine of Alexandria’s Confessions, written in 400 BCE, where he said:
“What then is time? If no one asks me, I know: if I wish to explain it to one that asketh, I know not: yet I say boldly that I know, that if nothing passed away, time were not; and if nothing were, time present were not.”
What Augustine is pointing out here is the inherent problem in explaining the slippery nature of time. We know exactly what time is — in fact, we are unable not to understand how it flows in our own lives — but when we try to define it in precise terms, it eludes us. He speaks of “if nothing passed away, time were not” that could, in a sense, describe how the second law of thermodynamics defines time’s arrow. We know time passes because things change in a certain way as time passes.
Relativity, Worldlines, and Worldsheets: Moving through space-time
Understanding how time travel works within string theory would require a complete understanding of how the fabric of space-time behaves within the theory. So far, string theory hasn’t exactly figured that out.
In general relativity, the motion of objects through space-time is described by a worldline. In string theory, scientists talk about strings (and branes) creating entire worldsheets as they move through space-time.
Worldlines were originally constructed by Hermann Minkowski when he created his Minkowski diagrams, shown in topic 6. Similar diagrams return in the form of Feynman diagrams (see topic 8), which demonstrate the worldlines of particles as they interact with each other through the exchange of gauge bosons.
In string theory, instead of the straight worldlines of point particles, it is the movement of strings through space-time that interests scientists, as shown in the right side of Figure 16-1.
Notice that in the original Feynman diagram, shown on the left of Figure 16-1, there are sharp points where the worldlines intersect (representing the point where the particles interact). In the worldsheet, the virtual string exchanged between the two original strings creates a smooth curve that has no sharp points. This equates to the fact that string theory contains no infinities in the description of this interaction, as opposed to pure quantum field theory. (Removing the infinities in quantum field theory requires renormalization.)

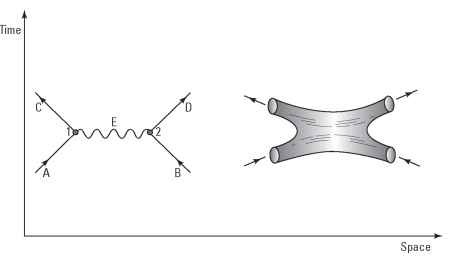
Figure 16-1:
Instead of a world-line (left), a string creates a worldsheet (right) when it moves through space.
One problem with both quantum field theory and string theory is that they are constructed in a way that gets placed inside the space-time coordinate system. General relativity, on the other hand, depicts a universe in which the space-time is dynamic. String theorists hope string theory will solve this conflict between the background-dependent quantum field theory and the background-independent general relativity so that eventually dynamic space-time will be derived out of string theory. One criticism (as discussed in topic 17) is that string theory is, at present, still background-dependent.
The competing theory, loop quantum gravity, incorporates space into the theory, but is still mounted on a background of time coordinates. Loop quantum gravity is covered in more detail in topic 18.
Hawking’s chronology protection conjecture: You’re not going anywhere
The concept of time travel is often closely tied to infinities in the curvature of space-time, such as that within black holes. In fact, the discoveries of mathematically possible time travel were found in the general relativity equations containing extreme space-time curvature. Stephen Hawking, one of the most renowned experts in looking at space-time curvature, believes that time travel is impossible and has proposed a chronology protection conjecture that some mechanism must exist to prevent time travel.
When black holes were first proposed as solutions to Einstein’s field equations, neither Einstein nor Eddington believed they were real. In a speech to a Royal Astronomical Society, Eddington said of black hole formation, “I think there should be a law of nature to prevent a star from behaving in this absurd way!”
Although Hawking is certainly comfortable with the idea of black holes, he objects to the idea of time travel. He proposed his chronology protection conjecture, which states that there must be something in the universe that prevents time travel.
Hawking’s sometimes collaborator, Oxford physicist Roger Penrose, made the much more guarded claim that all singularities would be protected by an event horizon, which would shield them from direct interaction with our normal space-time, known as the cosmic censorship conjecture. This would also potentially prevent many forms of time travel from being accessible to the universe at large.
One major reason time travel causes so much trouble for physics (and must therefore be prohibited, according to Einstein and Hawking) is that you could create a way of generating an infinite amount of energy. Say you had a portal into the past and shone a laser into it. You set up mirrors so the light coming out of the portal is deflected back around to go into the portal again, in tandem with the original beam you have set up.
Now the total intensity of light coming out of the portal (in the past) would be (or have been) twice the original laser light going in. This laser light is sent back through the portal, yielding an output of four times as much light as originally transmitted. This process could be continued, resulting in literally an infinite amount of energy created instantaneously.
Obviously, such a situation is just one of many examples why physicists tend to doubt the possibility of time travel (with a few notable exceptions, which I cover throughout this topic). If time travel were possible, then the predictive power of physics is lost, because the initial conditions are no longer trustworthy! The predictions based on those conditions would, therefore, be completely meaningless.
