Introduction
The orbit determination problem has its origin in the early efforts of solar system astronomers attempting to describe the motions of the planets and comets as they orbit the Sun. In these studies, the observations of the bodies, as observed from the surface of Earth, were fit to a path through the heavens that was completely described by six parameters. The foundations of modern estimation theory evolved from the early attempts to develop techniques to determine the six fundamental orbital parameters. Three of the parameters determine the orientation of the orbit or trajectory plane in space, and three locate the body in the orbital plane. These six parameters are uniquely related to the position and velocity of the satellite at a given epoch. Six appropriately selected observations will yield a solution for the trajectory. This is the classic orbit determination problem in which there is a match between the number of observations and the parameters to be determined. However, when the number of observations exceeds the number of parameters to be assigned, special techniques were required to allow using all observations. One solution to this problem was the method of least squares, which was proposed by Gauss in 1795 before his twentieth birthday. In an independent study, Legendre published a similar method in 1806 that led to considerable early debate about who originated the method. This early activity was followed by a period of intense study, culminating in the current theory for estimating dynamic parameters using observations corrupted by random measurement error.
During the past two decades, the requirements for highly accurate determinations of the orbits of near-Earth satellites have been driven by the evolution of the fields of satellite geodesy and satellite oceanography. The ability to use satellite altimeter measurements to obtain accurate, globally distributed, and temporally dense observations of a satellite height as it traverses the ocean surface has opened a new era in oceanography. The ability to use accurate range and range-rate measurements between an orbiting satellite and tracking systems located on Earth’s surface has provided a dramatic improvement in the ability to monitor tectonic surface deformation and subsidence and to monitor small but important changes in Earth’s rotation. These same measurements, along with satellite-to-satellite measurements, are providing unparalleled views of Earth’s gravity field and the gravitational signals from temporal variations in Earth’s mass distribution. The advances in each of these fields is tied to the advances in our ability to determine, at high accuracy, the path followed by an Earth-orbiting satellite. The methodology whereby this task is accomplished is referred to as precision orbit determination (POD).
In alternative applications, the recent advances in the spatial resolution of orbiting microwave and multispectral imaging systems has stimulated the requirements for accurate near-real-time orbits. These requirements along with the operational challenges of space object catalog maintenance to support collision avoidance in spacecraft operations has stimulated the need for accurate orbit prediction. The improvements in our knowledge of the models for the forces that influence a satellite’s motion along with the dramatic improvement in computational capability has opened a new era in determining and predicting the orbits of near-Earth satellites.
The Orbit Determination Concept
The solution of the orbit determination problem involves four fundamental elements: (1) a set of differential equations that describes the motion of the satellite; (2) a numerical integration procedure to obtain a solution of the differential equations; (3) accurate observations of the satellite’s motion; and (4) an appropriate estimation method that combines the results of the first three to yield an estimate of the satellite’s position, velocity, and appropriate model parameters (e.g., the drag coefficient). The basic procedure starts with an initial model of the trajectory of a satellite during some time interval. This initial orbit will be incorrect due to errors in the estimate for the starting point, deficiencies in the mathematical model for the forces acting on the satellite, and errors in the parameters used in the model. To correct the model, independent observations of the satellite’s motion must be obtained. These observations generally measure only some component of the motion, such as the distance or rate of change of the distance between the satellite and a ground-based tracking station. Measurements of the full three-dimensional position or velocity are usually not available, but as long as the observations depend on the satellite’s motion, they contain information that helps to determine the orbit. The evolution of the satellite’s position and velocity must be consistent with both the physics of the mathematical model and the sequence of observations, which constrains the orbit estimate to a specific solution.
The observations must also have a corresponding mathematical model to be usable in the orbit estimation problem. The observation model depends on the satellite’s motion, and also on the orientation of the spacecraft and the motion of the observing station. The measurement model must relate the location of the tracking instrument to the spacecraft’s center of mass, which may change with time as onboard fuel is consumed. At the same time, the tracking station is on a rotating Earth. The observing ”station” may even be another orbiting satellite, such as a Global Positioning Satellite (GPS). Finally, the measurement model must account for various atmospheric refractive effects and other instrument effects.
Assuming that the measurements are reliable, the discrepancies between the computed observables and the real observations (called the residuals) contain measurement errors and the effects of errors in the initial conditions as well as deficiencies in the dynamic and observational models. Through a linearized least-squares solution process discussed later, the initial conditions and selected model parameters are adjusted to minimize the residuals. Considerable experience is required in choosing the model parameters that are best suited for adjustment. The mathematical models will always be imperfect in some respects, and the adjusted parameters are chosen for their ability to compensate for the deficiencies. The orbit is then recalculated on the basis of improved initial conditions and parameters, the observations are again compared with their computed counterparts, and the initial conditions and parameters are adjusted again. During this iterative process, unreliable observations can be identified and removed. Given a set of observations that contain sufficient information, the adjustments become smaller and smaller with each iteration, and the process is judged to have converged when a satisfactory and stable orbit solution is obtained.
The advent of the GPS and space-qualified GPS receivers have allowed continuous kinematic (i.e., purely geometric) positioning of satellites. However, the dynamic techniques discussed here still tend to provide the best results.
Dynamics of Satellite Motion
The precise trajectory of a satellite has generally been obtained by integrating Newton’s dynamic equations of motion by numerical methods (1). The mathematical representation of the motion of the center of mass of a spacecraft is given by
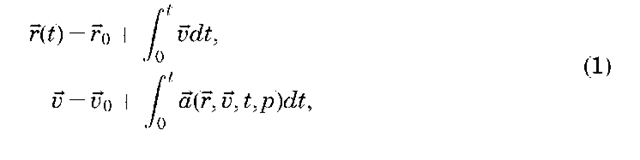
where t is time; r and v are the position and velocity vectors of the spacecraft’s center of mass whose initial values are r0 and V0 at time to; ~ is the acceleration (force per unit mass) of the spacecraft; and p represents all of the parameters that are employed in the models for the reference frame, the forces, and the observations. The arc length is the time interval from the initial point to some chosen final time. This may be several hours, a day, several days, or longer.
The forces acting on the satellite can be broadly classified as either gravitational or nongravitational. Among the gravitational forces, the two-body term (where the central body is assumed to be perfectly spherical) dominates the orbital motion by far. As a consequence, an orbit is well characterized by the Keplerian elements of an elliptical orbit (2,3). Figure 1 illustrates the geometric properties of the usual set of orbital elements used to describe the motion of a satellite in orbit about the Earth. The satellite height is characterized by the orbit’s semimajor axis a, the variation in the radial distance due to the ellipticity of the orbit (the eccentricity e), and the angular distance n (the true anomaly) from the point of closest approach in the orbit (called the perigee). Other angular measures besides n are used to relate time and the motion of the satellite along the orbit, including the eccentric anomaly E and the mean anomaly M. The tilt and orientation of the orbital plane are given by the inclination i and the longitude of the ascending node O. These two angles are related to the out-of-plane components of the orbit. The argument of perigee w is the angular distance along the orbit from the equatorial plane to the perigee, which determines the orientation of the long axis of the elliptical orbit within the orbital plane. The motion of a satellite in Earth orbit is principally characterized by these six orbital elements; the satellite is moving along an elliptical orbit within a plane that tends to precess slowly in space.
The Earth’s gravity field is, however, not perfectly spherical, and undulations in the gravity field, corresponding to the variations in Earth’s shape and density (discussed in other articles), cause perturbations from perfectly elliptical motion (4,5). In addition, perturbations are caused by the gravitational attraction of the Sun, Moon, and planets. For highly precise applications, the effects of general relativity, principally the precession of perigee and the relativistic effects on the observations, must also be considered.
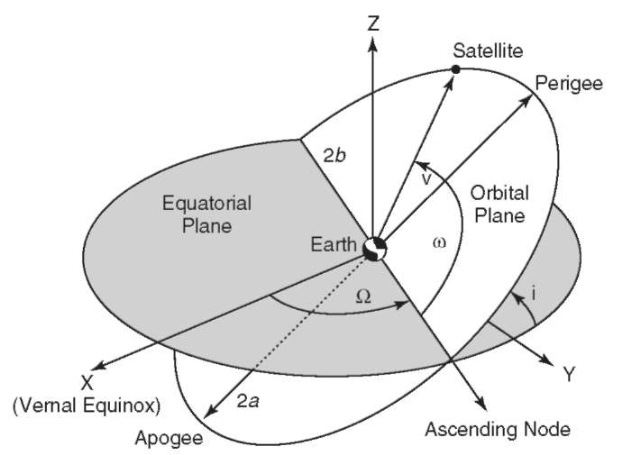
Figure 1. The elements of an elliptical orbit: semimajor axis a, inclination i, longitude (or right ascension) of the ascending node O, argument of perigee w, and true anomaly v. The eccentricity e relates the semimajor axis a to the semiminor axis b through the expression e2 = (a2 — b2)/a2.
The nongravitational perturbing forces (also known as surface forces) can be broadly classified into the categories of atmospheric drag and radiative pressure (6). Atmospheric drag is typically the greatest concern for artificial satellites because the atmosphere constantly dissipates energy from the orbit. In addition, there are large, sometimes rapid, variations in the atmospheric density at lower altitudes due to geomagnetic activity and solar storms. Radiative pressure includes the effects of direct solar light pressure on a satellite, indirect reflected light and reemitted heat from Earth, and heat emitted by the satellite itself. Finally, the satellite may be subjected to thrust from onboard propulsion or attitude control systems.
Orbit Estimation Problem
As noted earlier, knowledge of the forces acting on a satellite is imperfect, and the initial conditions required to start the integration cannot be known exactly. Observations of the position or velocity of the satellite must be obtained and incorporated into an orbit determination procedure that estimates these initial conditions and corrections to the parameters in the force and measurement models. Starting with estimates for the initial satellite position and velocity, the orbit is predicted for the times of the observations. Using a model for the measurement based on a priori estimates for the tracking station position, Earth orientation, atmospheric refractive effects, and measurement biases, a ”computed observation” G is formed and compared to the actual observation Y. The measurement residual Y — G is an indication of the mismatch between the mathematical model and the actual orbit, as illustrated in Fig. 2. Using an appropriate estimation procedure, the residuals from the data fits can be used to improve the estimates for the initial satellite state, as well as various parameters in the force or measurement model. Clearly, the more observations available and the more accurate they are, the better the orbit can be determined.
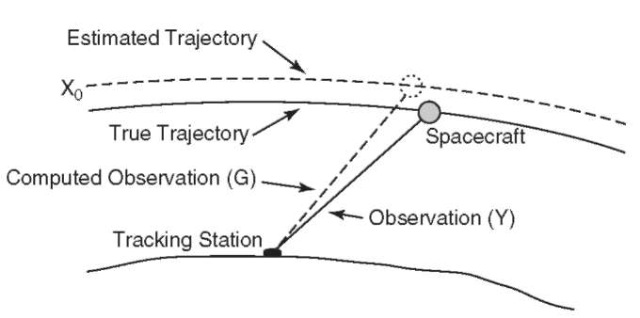
Figure 2. The orbit estimation problem. An observation Y, such as the range to the satellite, is compared to the range G computed from the numerically integrated satellite position to compute a residual Y — G. With many such observations, the initial conditions X0 and other model parameters are iteratively improved to bring the estimated orbit closer to the true orbit by minimizing the residuals in a least-squares sense.
This is a complex and nonlinear estimation problem that is usually linearized and solved numerically through an iterative method (7-9). This may be a “batch” process in which all of the measurements within the arc are combined to form the estimates of the initial conditions and the other force and measurement model parameters. Various “sequential” methods are also available in which the orbit and model parameter estimates are updated as soon as new data are available. The fidelity of the models for the dynamics and the measurements, the precision of the tracking data, and the quality of the orbit determination technique determine the accuracy of the resulting satellite ephemerides.
State Equations
As defined, the state vector is composed of all dependent variables or constant parameters required to define the time rate of change of the state of a dynamic system. By this definition, the re-dimensional state vector X can be expressed as follows:

and the state equations become
![]()
When X0 in Equation 3 is specified, the motion of the dynamic system will be determined uniquely by the solution to Equation 3. This solution can be expressed formally as
![]()
In the usual orbit determination problem, X0 will not be known perfectly and, consequently, the true solution X(t) will differ from the nominal solution X(t), obtained by using the specified initial state X. As a consequence, observations of the motion must be made to determine the true motion.
The Observation-State Relationship
Usually, the state vector X(t) cannot be observed directly. Instead, the observations will be a nonlinear function of the state. The observations are influenced by random instrumental errors. As a consequence of these points, the observation-state relationship can be expressed as

where Yt is a p-vector of observations at the time epoch tt, G(Xt, b, t^isa p-vector of nonlinear functions, b represents the constant parameters that appear in the
observation-state relations, and e; is a p-vector of observation errors. As an example, the observation may be the range between a tracking station and the satellite and in this case, Equation 5 would be expressed as
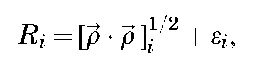
where p = r — rg, r is the location of the satellite’s laser reflector and rg is the location of the laser ranging station. For this case, Equation 5 will be a scalar observation-state relation at time tt. The quantity Rt will be obtained as the result of a direct measurement of some physical quantity.
More than one quantity may be observed in a given epoch, that is Yt may consist of measurements of range, range rate, azimuth, and elevation, where the observed quantities are measured from some observation point on the Earth’s surface or from another satellite. The actual physical measurements are physical quantities such as time of flight, phase, or frequency. These measurements can be used to infer range, biased range or range rate, respectively.
If p is the number of observations and n is the number of parameters to be estimated, the following comments can be made regarding the observation-state relationship expressed in Equation 5:
1. At any time epoch, Y will be smaller than X;, that is, p<n, for the orbit determination problem.
2. Furthermore, even if p = n, X; cannot be correctly determined from Equation 5 unless e = 0, that is, unless the observations are perfect and unless certain observing conditions are met.
To overcome these limitations, a large number of observations, distributed over the arc of interest, are acquired. The information used for estimating the initial state can be expressed as
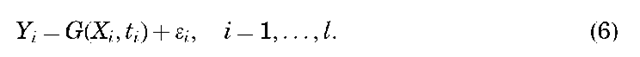
Because Xt = @(X0, t0, tj) from Equation 4, it follows that Equations 6 will represent l x p equations in (l x p x n) unknowns, that is, the unknown components of the observation error and the initial state. Because the number of equations is fewer than the number of unknowns in Equations 6, some additional criterion must be adopted for choosing X0. One frequently applied approach is to select the estimate of the state at t0, that is, X0, to minimize the error in the estimate of the initial state. Implementation of this criterion leads to the estimate of X0 based on either a least-squares error criterion or a statistically based criterion such as the minimum variance or maximum likelihood estimation criterion.
The difficulties of obtaining an estimate of X0 using Equations 4 and 5 lead to a nonlinear iterative approach based on using linear estimation techniques. This procedure, outlined below, is described in detail by Tapley et al. (10).
Linearization of the Nonlinear Problem
If the true value of the state X(t) and some initially assumed value of the state are sufficiently close throughout some time interval of interest, t0<t<t1,a Taylor series expansion about the initially assumed, or nominal, trajectory at each point can be used to linearize the nonlinear problem. To accomplish this, let
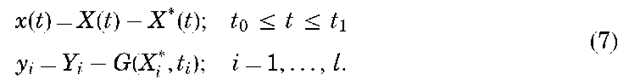
Then substituting Equations 7 in Equations 3 and 5, expanding in a Taylor’s series, and neglecting terms of 0J(X; — XX*)2], the following results are obtained:
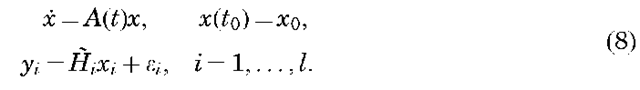
In Equation 8,
![]()
The unknown state, X0 is replaced by the unknown state deviation xk, and the nonlinear estimation problem is replaced by an estimation problem in which the observations are related linearly to the state and the state is propagated by a system of linear equations that has time-dependent coefficients. The quantity x(t) to be estimated, is the deviation from the reference solution X*(t). Equations 3 must be integrated using some initial value X*0 to obtain a reference solution for evaluating A(t) and i?;.
Reduction of Observations to a Single Epoch
To reduce (l x n + m) unknowns in Equations 8 to m + n unknowns where l is the number of observation epochs, n is the number of parameters in x, and m is the number of observations errors, all of the state variables x; are expressed as a function of the state at a single epoch, say xk. To this end, note that the solution of the first of Equations 8 can be expressed as
![]()
where F(t;, tk) is the state transition matrix, where
![]()
The state transition matrix satisfies the following differential equation (11):
![]()
where A(t) is defined in Equation 9. Using Equation 10, the system of Equations 8
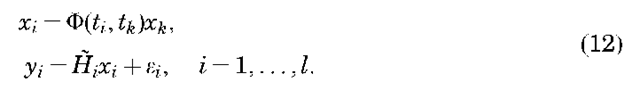
Now, if the first of Equations 12 is used to express each state xi in terms of the state at some general epoch tk, and by defining Hi = HliF(ti, tk), the second of Equations 12 can be expressed (dropping the subscript i)as

Equation 13 represents a system of m equations in m + n unknowns where m>n. When e = 0, any n of Equation 13 that are independent can be used to determine xk. For the general case, e O 0 and some further criterion, such as least squares, maximum likelihood, or minimum variance must be specified to determine xk.
Because each observation has an unknown error, there will always be m knowns (e.g., the observations y) and m + n unknowns (e.g., the m observation errors e and the n unknown components of the state vector xk). To resolve this problem, we follow the method ofleast squares (12,13). In this approach, the best estimate for the unknown state vector xk is selected as the value xk that minimizes the sum of the squares of the calculated values of the observation, errors, that is, if 8k is any value of xk, then e’ = y — Hdk will be the m calculated values of the observation residuals corresponding to the value dk. Then, the best estimate of xk will be the value that minimizes the performance index where
![]()
For a minimum of this quantity, it is necessary that (7)

Equation 15 are referred to as normal equations that represent a system of n linear algebraic equations. If the n x n matrix (HTH) has an inverse, the solution can be expressed as

In the algorithms before, it is assumed that each observation is of equal importance. If some observations are more accurate than others, the more accurate observations should be assigned a higher weight in processing the data. Typically, we use W as a diagonal m x m matrix, where a zero diagonal element implies that the corresponding observation is being neglected. This weighting matrix may also contain off-diagonal elements when the observations are correlated in some way. With this refinement, Equation 16 becomes
![]()
If there is an a priori estimate of the initial state, referred to as x0, and, an initial estimate of the error P0, then the estimate of the state deviation at t0 can be
obtained as follows:
![]()
Finally, Swerling (14) used a well-known identity to invert the final matrix on the right of the equality in Equation 18 algebraically to obtain this following sequential form of the estimation algorithm, where at time tk,
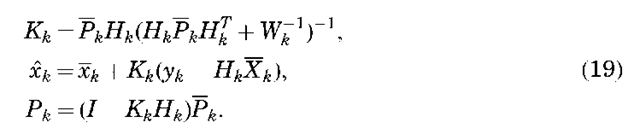
The estimate at tk is propagated forward to tk +1 by using the expressions
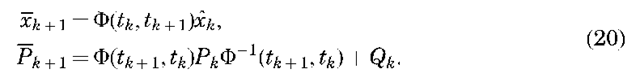
For application to linear dynamic systems, the algorithm given by Equations 19 and 20 was placed on a sound statistical basis by Kalman (15) and the algorithm was extended to estimating nonlinear dynamic systems by Kalman and Bucy (16) and Bucy (17). In applying the sequential algorithm to nonlinear systems, the truncated Taylor series expansion about a reference solution, generated from complete nonlinear system dynamics, is used to obtain a linear approximation of the deviation from the reference.
Applications
During the past several decades, considerable progress has been made in the area of precision orbit determination for geodetic satellites such as LAGEOS, STARLETTE, TOPEX/POSEIDON, and ERS-1. These satellites have been used to support studies of the gravity field of Earth, its rotation and shape, ocean circulation, and tides, and the accurate determination of the location and motion of the tracking stations can be used to establish a geocentric reference frame and monitor its temporal variation (18,19). The tracking and orbit determination requirements of these missions vary considerably, but orbital accuracy is a fundamental requirement for the success of each.
Advancements in determinating precise orbits received considerable stimulus from initiation of the TOPEX/POSEIDON (T/P) ocean altimeter mission (20). A description of the factors involved in this activity can be used to illuminate the applications of the POD algorithm described in the previous discussion. Accurate determination of the satellite position with respect to the Earth’s mass center allows using the satellite altimeter data to monitor sea surface topography. This topography can then be combined with knowledge of the marine geoid to study the major geostrophic currents and to monitor the rise in mean sea level, both of which are important in understanding global climate change. The ability to determine the radial component of the satellite orbit at sufficient accuracy to exploit fully the centimeter level precision of the radar altimeters requires both high-fidelity force models to describe the satellite motion and accurate tracking data that are well distributed temporally and geographically. The techniques described in the previous discussion can be used to combine these two inputs to achieve the requisite orbital accuracy.
Tracking Systems. A fundamental requirement for determining orbits that have the requisite accuracy for geodetic satellites is accurate, globally distributed tracking. In the T/P mission, three different types of tracking are available. These systems are the satellite laser ranging SLR (18), the DORIS Doppler range-rate system (21), and the GPS phase measurement system (22). Although highly accurate, the quantity and distribution of the SLR tracking data are influenced by weather, operator scheduling, and sparseness of ranging stations. The all-weather coverage provided by the DORIS system provides additional temporal and geographical coverage to complement the absolute accuracy of the SLR tracking. The combination of the SLR and DORIS tracking data sets for T/P provides nearly continuous geographical and temporal coverage from highly precise tracking systems. The GPS data collected by the GPS receiver carried onboard T/P provided highly accurate data that had very dense spatial and temporal coverage when the GPS selective availability (SA) mode was not implemented (23). This data set has provided a valuable source for model improvement and independent orbit accuracy evaluation for T/P, and the use of GPS receivers onboard satellites is expected to become widespread in the future.
The Satellite Laser Ranging System. The SLR system, which has been one of the primary geodetic tracking systems for nearly two decades, serves as the baseline tracking system for the T/P mission. The SLR measurement is the time for an optical pulse to travel from the tracking system transmitter to a reflector on the satellite and back to the tracking system. This measurement represent the state of the art in satellite tracking accuracy; its accuracy is better than one centimeter for the best instruments. In addition, the optical wavelengths are not influenced by ionospheric refraction, and the effect of water vapor is much smaller than for radiometric tracking systems. Because SLR observations provide a precise, direct measurement of the absolute range from the tracking station to a satellite, they provide good resolution of all three components of the spacecraft position with respect to the tracking network.
The DORIS Tracking System. DORIS is a one-way, ascending Doppler system that uses a set of ground beacons that broadcast continuously and omnidirectionally on two frequencies of 2036.25 and 401.25 MHz. A receiver onboard the satellite receives this signal and measures the Doppler shift, from which the average range rate of the satellite with respect to the beacon can be inferred. Average range rate is here defined as the range change across a finite count interval, usually 7 to 10 seconds for DORIS. The use of dual frequencies allows removing the ionospheric refraction. Using more than 50 beacons operating all over the world, the DORIS data provide the frequent, accurate observations of satellite motion necessary to help mitigate the effects of radiative pressure and drag forces. Thus, the DORIS system is an excellent complement to the highly precise SLR system and plays an essential role in meeting the rigorous tracking demands of the T/P mission.
The GPS Tracking System. GPS data are provided by the 24-satellite constellation of Global Positioning Satellites. This system was deployed to satisfy the real-time navigational requirements of the Department of Defense, but a number of uses of the data have been developed for highly accurate position determinations. By collecting the data using receivers located on the ground, position determination at the 1-cm level on the Earth’s surface has been demonstrated. The combination of data from these accurate surface locations and the GPS measurements collected onboard the T/P satellite provides a unique data set for orbit determination or model improvement. The GPS measurement used for precise POD is the measured phase of the carrier signal, which is equivalent to a biased range measurement accurate to approximately a centimeter. Using as many as 8 to 10 GPS satellites and multiple ground stations visible to T/P at any time, a large number of observations is possible. The range measurements are biased and the clocks on the various GPS satellites and on T/P are not synchronized, but the data density provides adequate information to remove these error sources and still provide an accurate orbit for the lower satellite. The decision of the Department of Defense to allow use of GPS data at full precision provides a powerful data set for current and future geodetic missions.
Terrestrial Reference System. An important consideration in the success of the POD function is the ability to define and maintain an accurate terrestrial reference frame because this forms the reference for the location of the tracking systems described before. The international network of satellite laser ranging systems has provided the foundation for satellite geodetic advances during the past two decades. The addition of the densification from GPS and DORIS tracking systems provides input for determining and maintaining the International Terrestrial Reference Systems (ITRS). These tracking data are crucial to the current reference frame definition and provide the precise height control required to ensure the utility of the T/P results for long-term studies of ocean surface change. In the current determination of the ITRS, the accuracy of the positions of the better tracking sites is estimated at the centimeter level, both relative to the stations in the network and in an absolute sense with respect to Earth’s center of mass.
Force Model Improvement. To achieve the current accuracy in POD, an intensive effort was required to improve the satellite force models, with particular emphasis on the geopotential and surface force models. To reduce the effects of atmospheric drag and the influence of errors in the ocean tide model, the TOPEX/ Poseidon satellite was placed into a circular orbit at an altitude of 1336 km and inclination of 66°. For satellites at lower altitudes, atmospheric drag is an important source of orbit error and is currently limited by knowledge of atmospheric density variations, particularly when solar activity is at its maximum. For satellites where the atmospheric drag is not a problem, radiative pressure from sunlight emitted by the Sun or heat reradiated by the spacecraft become important forces.
Gravity Model Improvement. Error analysis of the best general gravity models available when the T/P mission was initiated, for example, the GEM-10B model (24), predicted radial orbital errors that approached 100 cm for the T/P orbit. Based on the observation that the gravitational model error was the primary error source, an intense effort aimed at improving the gravitational model was initiated by the TOPEX project. This effort spanned almost a decade and led to a dramatic improvement in Earth’s gravitational model, especially in the long-wavelength components that are most important to satellites. Further improvement was obtained when the GPS tracking data from the T/P satellite receiver, along with additional SLR and DORIS tracking data, were used to produce the JGM-3 gravitational model (25). Figure 3 summarizes the improvement in gravitational models for T/P from GEM-10B to JGM-3, the model currently used for T/P orbit production. For an altimeter satellite, the radial or height accuracy is the most critical to using the altimeter data.
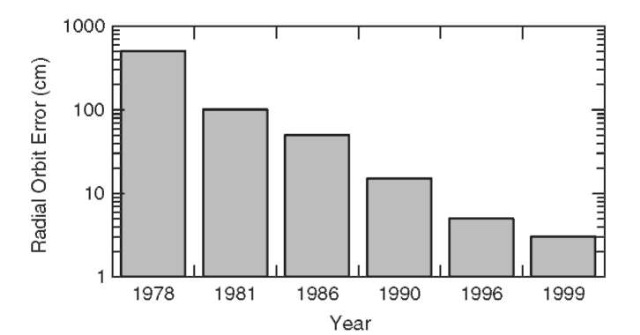
Figure 3. Progress in the accuracy of the radial orbital component since 1978 for altimeter satellites such as TOPEX/POSEIDON.
Nongravitational Forces. Because of the significant improvement achieved in the gravitational model, nongravitational force models have become a comparable error source. The dominant effects are those due to drag and to solar, terrestrial, and thermal radiative pressure (Fig. 4). To meet current POD requirements, models are required to account for the satellite’s complex geometry and attitude variations and its thermal and radiative surface properties. Typically, a relatively simple and computationally efficient model suitable for precise orbital computations is used to represent the spacecraft, although some applications require more detailed models that account for the forces acting on the individual surfaces of the spacecraft (26). The attitude of the spacecraft is modeled to account for the variations in area that result as the spacecraft attempts to maintain a specific orientation in space. The spacecraft attitude is especially critical for correcting the tracking measurements, such as SLR, DORIS or GPS, to the satellite’s center of mass. Even though complex surface force models are employed, considerable error remains that would severely limit orbital accuracy, if not accommodated. One approach consists of estimating various empirical accelerations to absorb the errors in the surface force model that still remain (27). This allows further reduction in orbital errors due to surface force modeling deficiencies. As an alternative to modeling surface force effects, the application of three-axis accelerometers to measure surface force effects is being used on missions such as the CHAMP and GRACE gravitational mapping missions. In the future, we might expect surface-force compensation systems (so-called ”drag-free” satellites) to be employed, so that the satellite orbits are entirely unaffected by nongravitational forces.
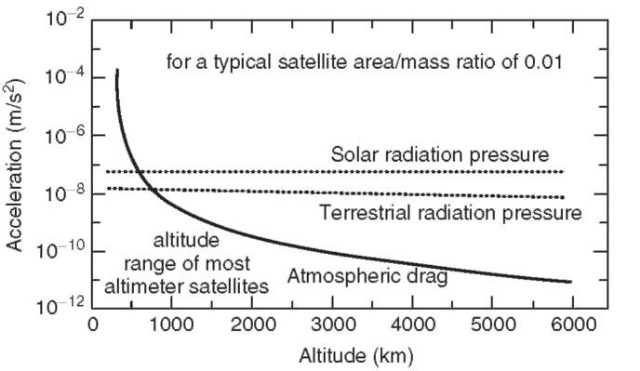
Figure 4. Relative size of nongravitational forces acting on a near-Earth satellite that has a typical area to mass ratio.
Summary
The techniques and tracking systems for computing accurate orbits for near-Earth geodetic and oceanographic satellites have undergone dramatic improvement during the last two decades. This improvement is exemplified by the orbital improvement for the TOPEX/POSEIDON orbit and for a number of other geodetic satellites. The orbital accuracies achievable when the T/P POD effort began were characterized by radial orbital errors at the meter level, but current accuracies are approaching the centimeter level. This improvement, which represents an approximately two order of magnitude increase in accuracy, has been achieved by a dramatic improvement in the accuracy and distribution of the tracking systems and the terrestrial reference frame, the use of the improved data in a sustained satellite force model development, and an extended effort to improve POD software systems. Because orbital accuracies for most geodetic satellites are routinely at the few cm level, the goal of achieving 1-centimeter accuracies for future satellite altimeter missions appears within reach.
