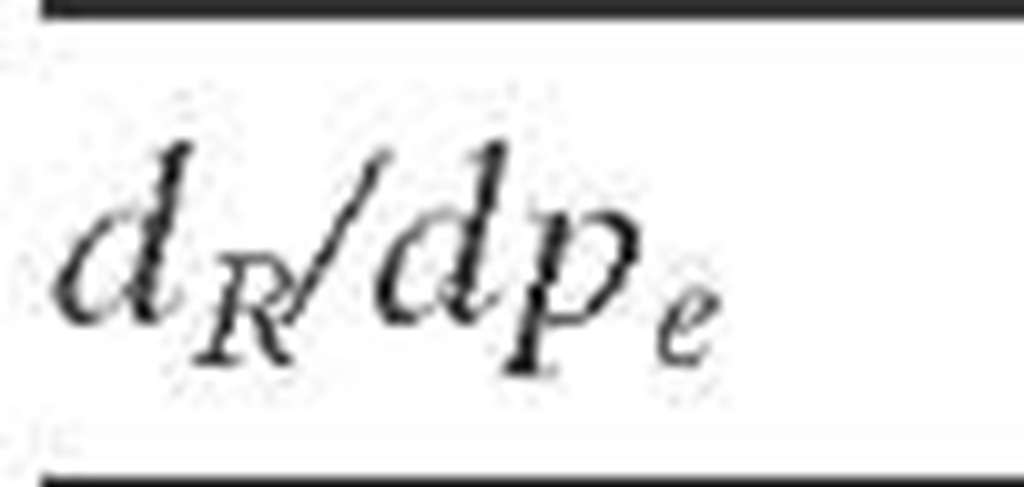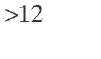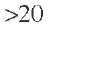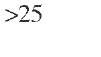Wetting Effects
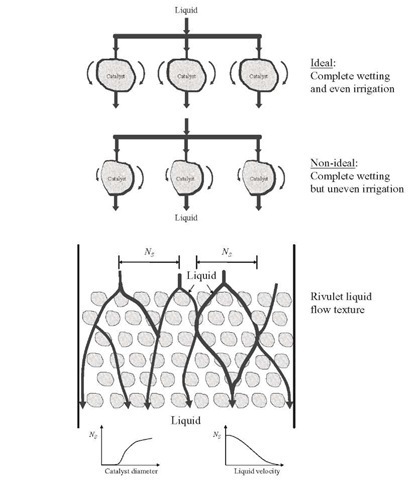
As mentioned before, the second condition for an ideal reactor is that all catalyst particles must contribute equally to the overall conversion. In TBR, each catalyst particle should therefore be surrounded by a flowing film of liquid. The flux of liquid and gas should be the same in any part of the bed cross section. However, a special situation may prevail, particularly at low liquid velocities, in which liquid flows preferentially through a certain part of the bed while gas passes predominantly through another part in the interstitial spaces that are not occupied by liquid. In the latter part there are catalyst particles that are not totally contacted by liquid reactant and hence do not contribute to the overall conversion (Figure 2.3). This situation leads to incomplete utilization of the bed and is known as macroscopic maldistribution of liquid or incomplete wetting- Its effect on the reactor scale is measured as contacting effectiveness or the catalyst utilization fraction [Eq. (2.35), Table 2.4].
Satterfield (1975) has shown that the contacting efficiency (CE) depends on the liquid mass velocity, which can be approximated by a power-law function with an exponent of roughly two- thirds [Eq. (2.36) ]. This correlation assumes that full catalyst utilization is achieved at liquid mass velocities equal to or greater than those required by meeting plug-flow criteria. Although the term incomplete wetting is appropriate in cases where some catalyst particles indeed remain dry, the term uneven irrigation is preferred. This problem aggravates by poor initial maldistribution of liquid in commercial reactors (e.g., inefficient reactor internals), but it can also be developed at low velocities even if the initial distribution is adequate.
On a particle scale, incomplete wetting is not very likely to occur under normal hydrotreating conditions in the sense of interfacial tensions because the hydrocarbon feedstocks used (i.e., viscous oil) generally tend to spread easily over the porous catalyst surface. This complete particle wetting does not mean optimal catalyst utilization. If liquid flow around the catalyst particles is very uneven, part of the liquid film of variable thickness covering them is not refreshed at a sufficiently high rate, and part of the catalyst particle may not be used as it should be, as illustrated in Figure 2.7 for the case of a pore with a diffusion-reaction process where the renewal of liquid is essential. Hence, complete wetting is an insufficient condition for an ideal reactor, whereas even irrigation appears to be a more stringent and descriptive requirement which correctly associates the phenomenon of liquid maldistribution with dynamic (flow-related) forces instead of with static force balance (interfacial tensions). Figure 2.3 shows that at the contact points between adjacent catalyst particles there are pockets of liquid that are stagnant. Mass transfer between these stagnant pockets and the flowing liquid has to occur by diffusion.
Satterfield and Ozel (1973) provided visual evidence of ineffective wetting in laboratory TBRs and showed downward flow of liquid in rivulets which tended to maintain their positions with time. It was also observed that some catalyst pellets were covered with trickling liquid film, whereas others were not, although being wet. It then seems reasonable to assume that the reaction rate is proportional to the fraction of external catalyst surface effectively (freshly) wetted by the flowing liquid, being expressed as effective wetting or catalyst wetting efficiency [Eq. (2.37)] . With respect to the internal wetting efficiency of catalyst pores (fw) , there is general consensus that pores are completely filled with liquid due to capillary forces, even in the presence of partial external wetting, except for heavy oils, for which some researchers have found that f w < 1.
TABLE 2.4. Equations for the Criteria for Wetting and Wall Effects
|
Criterion |
Eq. |
Criterion |
Eq. |
 |
(2.35) |
 |
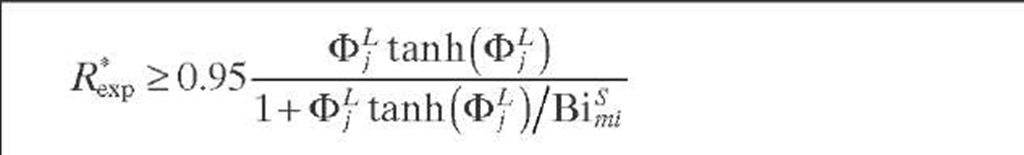(2.43) |
 |
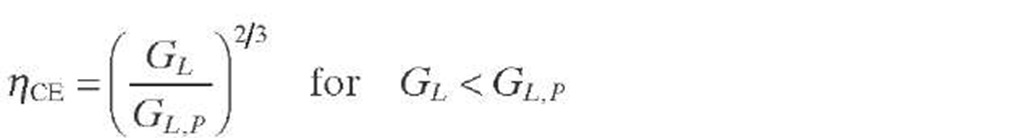(2.36) |
 |
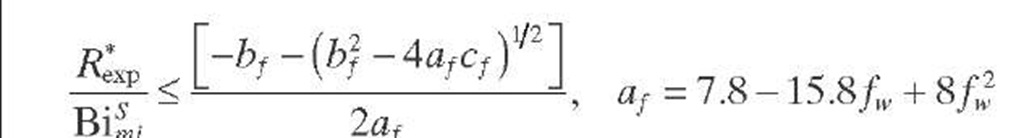(2.44) |
 |
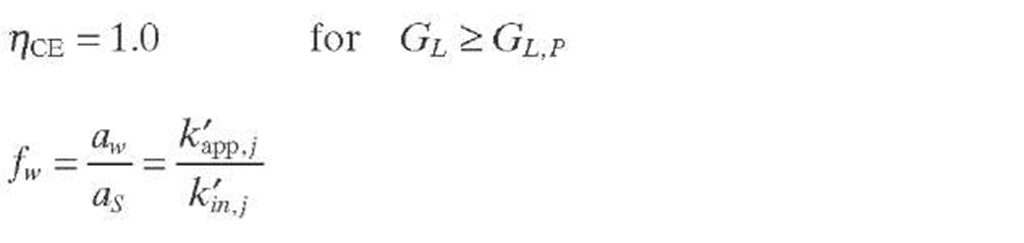(2.37) |
 |
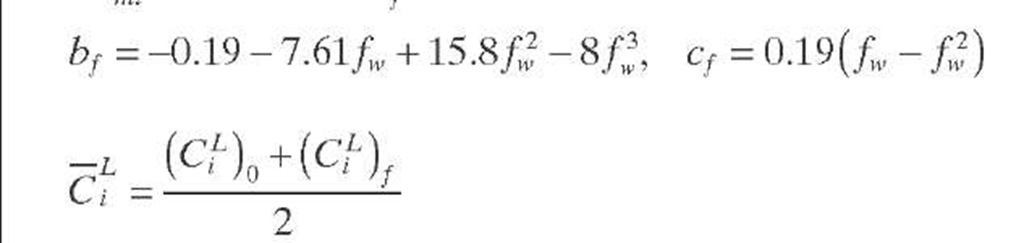(2.45) |
 |
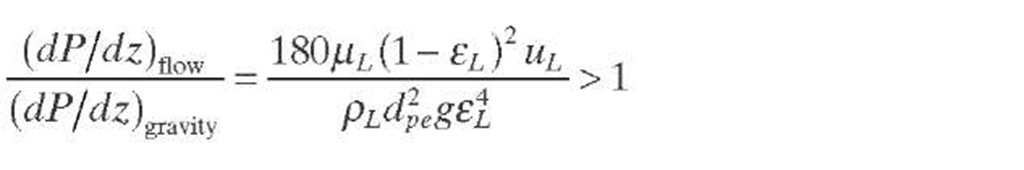(2.38) |
 |
|
 |
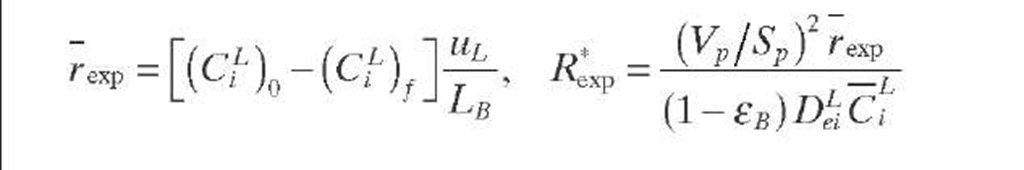(2.39) |
 |
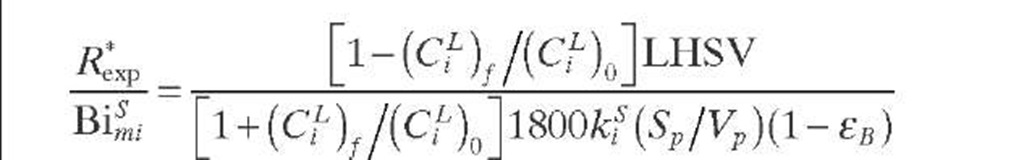(2.46) |
 |
(2.40) (2.41) |
 |
(2.47) |
 |
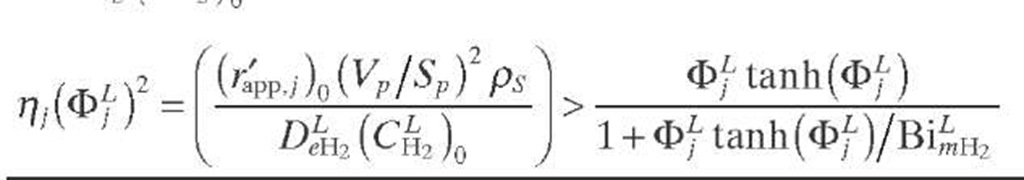(2.42) |
 |
(2.48) |
Figure 2.7. Effect of irrigation on catalyst utilization for a pore-diffusion-limited reaction and rivulet liquid flow texture at the bed scale in a TBR.
On a bed scale, nonhomogeneous liquid flow can be distinguished. Particularly at low liquid velocities with large catalyst particles, the liquid passes through the bed as small streams following different paths, the rivulets. The characteristic distance between adjacent rivulets (NS- is a function of catalyst particle diameter and liquid velocity, as indicated in Figure 2.7. This tendency of the liquid to bypass parts of the bed and thus to exclude catalyst particles from direct contact with flowing liquid is detrimental to reactor performance, this nonideal situation being incomplete wetting of the catalyst. As indicated before, the fraction of catalytic bed effectively wetted is a function of the initial distribution of liquid at the top of the reactor and its length-to-diameter ratio. This is more evident in the case of commercial reactors with large diameter, where the chances of channeling, low effective distribution, and so on, are greatly increased. About this last point, Baker et al. (1935) reported the need of some device for uniform initial distribution, since the flow from a single stream does not become uniform until the condition LB > 5dR is achieved.
The situation of liquid maldistribution showed in Figure 2.3 can be sustained if the flow of liquid is dictated largely by the force of gravity and influenced very little by frictional forces. In the opposite situation, the high pressure drop will force the liquid to spread over every interstitial channel available, so that the liquid will flow more uniformly through the entire bed cross section, thus improving contact with the catalytic surface. Hence, the condition for even irrigation in trickle flow may be stated as the predominance of impedance to flow over gravity, as expressed by Eq. (2.38).
Adequate wetting or even irrigation of catalyst may be obtained by assuming that eL = 0.15; therefore, the condition for even irrigation can be rewritten as in Eq. (2.39). W, known as the wetting number, compares frictional and gravitational forces, and its minimum value agrees very well with that reported by Gierman (1988) for a large quantity of experimental data [Eq. (2.40)]. It can then be established that the main variables dictating the uniformity of catalyst irrigation are the superficial liquid velocity, the particle diameter, and the kinematic viscosity of the liquid (vL = ^L/pL), being a particle size of particular importance. For less viscous feeds, small reactors may be operated under the condition of an optimally diluted catalyst bed.
For commercial-scale reactors, Henry and Gilbert (1973) and Sie and Krishna (1998) suggested that operating at Re << 10 will produce poor wetting. About 100% of catalyst utilization is found in industrial hydroprocessing reactors when they are operated at high mass velocities (>0.7g/s-cm2). For pilot-plant reactors, mass velocities are much lower (0.007 to 0.07g/s – cm-), which implies an operation with less than 100% catalyst utilization. According to Gianetto and Specchia (1992)- a contacting effectiveness factor of less than unity is almost certain when uL < 4 to 5mm/s.
A criterion to show whether the reaction under consideration is affected by partial wetting (fw < 1) was derived by Lee and Smith (1982) for catalyst particles in TBRs. Since the criterion is expressed in terms of observable quantities, it is applicable to limiting reactant in the liquid phase. The external surfaces of catalytic pellets are partially covered by liquid (fw < 1) when the criterion given by Eq. (2.41) is fulfilled. This criterion is valid for isothermal first-order reactions in PFRs when the reaction is diffusion limited (®L >> Bimi) and is based on the fact that m > rf when fw < 1. If this is not the case, the criterion given by Eq. (2.42) based on the Thiele modulus must be applied.
In cases when the reaction is limited by either the liquid- or gas- phase reactant, the influence of partial external wetting is considerably different. For first-order reactions limited by nonvolatile reactant in the liquid phase, as in hydrotreating operations, a criterion at the catalytic pellet level was formulated by Cassanello et al. (1992) – When the external wetting fraction is less than unity, the effectiveness factor may be lower than the factor corresponding to a completely liquid-covered pellet (%). Based on the fact that the effect of partial wetting is larger than 5% when n/% < 0.95, the criterion establishes that the impact of partial wetting is less than 5% and Eq. (2.43) is fulfilled. For liquid-limited reactions when the rate constant is unknown, the criterion given by Eq. (2.44) was proposed by Cassanello et al. (1992).
Naturally, for a limiting reactant in the liquid phase, if fw > 0.95, there is no influence of external wetting. Thus, Eq. (2.44) is applied when the external wetting efficiency is less than 0.95. Although Eq. (2.44) was developed by taking the observed reaction rate from a single catalyst pellet into account, its use can be extended to integral reactors by calculating R*xp with Eq. (2.45). As Eq. (2.45) can be written in terms of LHSV, the left-hand side of Eq. (2.44) is then developed to give Eq. (2.46).
It is important to point out that when the design of the distribution tray in commercial HDT reactors leaves a significant percentage of the top of the bed unwetted, it is expected that radial dispersion mixing of the liquid compensates for maldistribution by wetting the entire cross-sectional bed area (Jacobs and Milliken, 2000). Some reports have showed that diluting lab-scale multiphase FBR with fines can be effective for decoupling the kinetic behavior of the catalyst pellets from the reactor hydrodynamics. However, Tsamatsoulis et al. (2001) and Ramfrez et al. (2004) found that dilution of catalyst particles with inert fines does not guarantee full external catalyst wetting (not poor wetting) at all superficial liquid flow rates, because maldistribution of diluent particles may influence the conversion negatively, due to local bypassing of the catalyst pellets by the reactant stream.
The fraction effectively wetted is a function of the initial distribution of liquid in the reactor, superficial liquid mass velocity, and its length-to-diameter ratio, particularly in the case of commercial reactors. Simulations and experimental observations showed that nonuniform coverage of particles by liquid occurs particularly when liquid loads are low, as in the case of laboratory reactors. As we discuss in the next section, achieving complete uniform liquid wetting of the catalyst is desirable because it increases catalyst utilization and reduces the potential impact of any channeling, resulting in operations at a lower reactor temperature and thus a longer run length.
Wall Effects
Both hydrodynamics and intrinsic chemical kinetics affect the reaction rates. This means that when sizing a reactor, if its length is reduced, the representativeness of kinetic measurements obtained in the laboratory reactor will be lost. The only dimension that can be reduced a priori is the reactor width, but care has to be taken when the wall effect begins to become important. In downward-flow TBR, the liquid tends to move toward the reactor walls, which are not catalytically active. This excess of liquid flow near the wall gives rise to an appreciable spread in the residence time of the reactant.
The most common criteria to ensure uniform liquid distribution and hence to eliminate wall flow along a catalytic bed are based on a minimum value of reactor-to-particle diameter ratio. Table 2.5 summarizes some of these criteria. The wide variation in the values of dR/dpe ratio reported by different authors could be an effect of particle orientation in the bed (i.e., the method of catalyst loading affects the liquid distribution). It has also been reported that the lower the surface tension and density of liquid, the lower the wall flow (Saroha et al., 1988).
How small the dR/dpe ratio should be is not easy to know, since the smaller the reactor diameter, the more important the wall effect. The overall characteristics of the packed bed are different as the reactor diameter is reduced because the packing of particles is more open near the wall (high bed porosity) only by the presence of the wall surface, provoking a larger fluid velocity (channeling) and a lower catalyst bulk density. Near the wall the fluid velocities are greater and the conversions are lower as a result of the lower resistance to flow, causing an apparent lower activity for all the bed, which can be improved by better radial transfer. Therefore, the better isothermality in reduced-diameter reactors appears to more than compensate for the slight channeling loss to dR/dpe ratios as low as 4. If diffusion in the radial direction is sufficiently fast, the effect of the velocity profile might be diminished. Since diffusivities of liquids are too low to wipe out the effect of radial flow profiles, and the liquid phase rather than the gas phase determines HDT reactor performance, it is not possible to consider a beneficial effect of radial diffusion with low dR/dpe ratios. Furthermore, since the reduction in effective bed activity by the wall effect is more serious in trickle flow, larger ratios must be used for this operation.
To study the kinetics of highly exothermic heterogeneous catalytic reactions, dilution of catalyst with an inert material has frequently been used to work in the isothermal mode. A good practice is to dilute the catalyst with inert particles as small as dpe/10, so that fluid dynamics are dictated largely by the packing of the small inert particles and by the chemical kinetics of the active catalyst particles. Van den Bleek et al. (1969) proposed a general criterion in order to examine the possible influence of the amount of inert material (i.e., overdilution) on conversion in FBRs, on the basis that the influence of dilution on conversion can be neglected if the relative experimental error in the conversion is an order of magnitude larger than the dilution effect. This criterion makes it possible to determine the allowable degree of dilution in isothermal reactors with uniform dilution, which avoids the reaction mixture bypassing the catalyst, hence for allowable neglect of the dilution effect on the conversion in irreversible isothermal reactions [Eq. (2.47)]. For this criterion it is important to point out that care must be taken in estimating the real value of the dilution parameter (Z), especially in cases where the diameter of an inert particle is smaller than that of a catalyst particle.
For reactors larger than 1 i n. in diameter, Ross (1965) has reported that liquid maldistribution is an important problem. However, Henry and Gilbert (1973) have demonstrated no significant liquid distribution effect in their experiments with reactors up to 4 -n. in diameter. If an isothermal reactor operation mode is desired, the heat transfer effect is often more significant than the mass transfer effect. The resulting axial temperature gradient can only be avoided if the heat is transferred sufficiently faster from the catalyst particles to the reactor. This necessarily creates a radial gradient that will impose an upper limit on the diameter of the reactor. However, there will also be a lower limit on the reactor diameter because at some point the liquid flow close to the reactor wall will be more significant with respect to the flow at the center of the bed, so according to Doraiswamy and Tajbl (1974), if the radial aspect ratio dR/dpe > 4, good liquid distribution can be assumed and there are no adverse channeling and heat transfer effects at the reactor wall. Satterfield (1975) has reported that hydrodynamic problems associated with liquid distribution and wall flow decrease for a reactor diameter-to-particle diameter ratio above 10. Gierman (1988) has suggested a minimum value of 16 for this ratio, which would have been thought to be sufficient to ensure minimal liquid maldistribution and wall effects for intermediate petroleum feedstocks (°API > 20). However, heavy oils (20 > °API > 10) and bitumens (°API < 10) may exhibit coning and incomplete wetting of the catalyst even when the reactor diameter-to-particle diameter is 16 (Kwak, 1994).
The change in voidage near the reactor wall has been the subject of many experimental as well as theoretical investigations. Chu and Ng (1989) calculated local bed porosities and local specific surface areas using computer-generated model packings, which are columns randomly filled with uniform spheres generated by following the computer-simulated packing approach of Zimmerman and Ng -1986) – Their main finding was that the average bed voidage (or bed porosity) near the reactor wall reaches a value of unity, and the outer surface area of the particles per bed volume unit approaches a higher value than the average value in the interior of the bed if the wall surface is also considered. Because the greater average permeability in the wall zone tends to enhance the flow and the reactor wall itself produces flow retardation, the radial velocity profile presents a maximum at a location of one to a few particle diameters away from the reactor wall. These physical characteristics (bed voidage and specific area) influence the local fluid velocity and contribute thereby to deviations from the ideal plug flow when the ratio dR/dpe < 25.
By taking the data published by Herskowitz and Smith (1978a,b) and other authors into account, Gianetto and Specchia (1992) used the dimensionless group DLLBldR considered previously by Hoftyzer (1964) – and established that an acceptable liquid distribution could be obtained when Eq. (2.48) is fulfilled. If fluid dynamics and reaction kinetics are so closely interlinked that their effects on the conversion are inseparable, the only way to scale down a commercial- size reactor is to reduce the diameter while keeping the length unchanged. As long as the diameter is not reduced to the extent that wall effects begin to cause the packing to deviate from the unperturbed packing in a large-diameter reactor, the packing structure, the particle Reynolds number, and therefore the fluid dynamics should be identical to those in the commercial-size reactor. This approach is based on the notion that in a well- designed commercial reactor the situation in a horizontal plane within the bed is the same everywhere. Thus, the smaller pilot reactor is a hypothetical narrow vertical column cut out from the large catalyst bed. The minimum diameter of the pilot reactor is determined by the catalyst particle diameter, and this size dimension, together with the same commercial length, gives the smallest truly representative reactor that it is possible to obtain. Further reduction in length is possible as far as criteria to avoid axial dispersion effect allow. These considerations are implied to a lesser extent in the sizing of a typical pilot plant for fixed-bed processes: an LB/dR ratio of 50 to 250. From measurements of residence- t ime distribution in microreactors operated with gas, it has been confirmed that because of fast radial diffusion, the contribution of the wall effect is relatively insignificant, so its effect is negligible compared with axial molecular diffusion.
In summary, the wall effect (bed channeling) is caused by nonuniformities in the catalyst bed properties, which can be distinguished from other forms of liquid maldistribution (e.g., poor distribution tray design, sediment deposition on a catalyst bed). The liquid maldistribution occurring at the top of bed can be corrected with the bed depth, provided that the catalyst bed properties are uniform. Bed channeling works against this corrective action, however. As a result, reactor depths are often limited to 457 to 1067 cm to mitigate the impact of bed channeling on catalyst utilization. Therefore, the reactor wall will withdraw part of the liquid from the packing, introducing a complication both in the interpretation of experimental data on the distribution of the liquid and in performing calculations about the course of the liquid distribution. However, fortunately the liquid bypassing effect due to wall flow is not a significant concern in commercial TBRs, as the reactor-to-particle diameter ratios are very large, making this effect small enough to treat it as a correction to the distribution of the liquid over the cross-sectional area. Those effects of the wall in narrow reactors with full-sized catalyst particles and the axial dispersion in all the catalyst beds at low linear velocities are likely to remain important. Hence, particularly at high conversions and for reactions of high order, it is doubtful whether substantial downscaling of reactors will be possible without loss of accuracy and meaningfulness of results. The axial dispersion formed by wall flow will be significant only for cases where the conversion per pass through the reactor is high, and many errors introduced by this dispersion will result in an observed reaction rate expression that slightly underestimates the true reaction rate, leading to a slightly oversized commercial reactor design. The methods to reduce the wall flow are to control the dR/dpe ratio (see Table 2.5), to dilute liquid feedstocks in order to obtain low surface tension and density, and to increase the liquid and gas flow, which was also found to improve liquid distribution within the reactor.
TABLE 2.5. Rule of Thumb for Wall Effects
 |
Application |
Reference |
 |
For good liquid distribution without channeling and heat transfer effects at the reactor wall |
Kumar et al. (2001) |
 |
To gain isothermality |
Mears (1971) |
 |
For cutting down radial temperature gradients |
Doraiswamy and Tajbl (1974) |
 |
Practical rule to avoid the wall influence on the position of the dumped packing |
Hoftyzer (1964) |
 |
Decrease of hydrodynamic problems associated with liquid distribution and wall flow |
Satterfield (1975) |
 |
For particles 2 mm in diameter |
Larachi et al. (1991a,b) |
 |
From large and hollow particles with water-air flow at conditions of absorption column operation |
Baker et al. (1935) |
 |
Co-current trickle gas-liquid flow regime (0.1-10 MPa) |
Attou et al. (1999) |
 |
To control radial temperature gradients |
Butt and Weekman (1974) |
 |
To avoid wall flow |
Gierman (1988) |
 |
Gas continuous and trickling flow regimes, air-water at 25°C, 1 atm pressure; dR/dpe < 30, |
Herskowitz and Smith |
 |
catalyst particle sizes from 0.26 to 1.1 cm with granular, spherical, and cylindrical shapes; |
(1978a,b) |
 |
two columns of 4.08 and 11.4 cm I.D., LB=0-26 in a small column, 0-70 cm in a larger |
|
 |
column; uL=0.1-0.5 cm/s, uG=0.1-5.0; results with 10% of reproducibility |
|
 |
To minimize the nonuniformity of liquid flow distribution at elevated pressures |
Al-Dahhan and Dudukovic (1994) |
 |
Value proposed from the dependence of overall bed porosity and permeability on the ratio between bed and particle diameters |
Sie and Krishna (1998) |
 |
From large and hollow particles at flow conditions of absorption column operation |
Porter et al. (1968; Porter |
 |
and Templemen, 1968) |
|
 |
To avoid liquid bypassing along the wall |
Froment and Bischoff (1990) |
 |
Uniform liquid flow at equilibrium; glass beds 0.64-0.98 cm in size; trickling flow regime |
Specchia et al. (1974) |
 |
Wall flow less than 10%; pellets 0.64-0.98 cm in size (shape unknown); trickling flow regime without gas flow |
Prchlik et al. (1975a,b) |
 |
Nonreactive system with an incompressible single-phase (water) flow in porous media; pseudosteady (laminar flow) operation mode; spheres with almost uniform size from 0.024 to 0.160 cm I.D. and a density of 2.5 g/cm3; experimental tubes with 0.273, 0.491, 0.802, 0.957, and 1.89 cm I.D; value obtained from measured radial velocity profiles assuming that there is a reasonably large inert part of the bed where flow is even |
Chu and Ng (1989) |
 |
To avoid bypassing (e.g., wall effects) to become significant |
Sie (1991) |
 |
Negligible heat transfer resistance at the wall |
Mears (1971) |
The gas fraction in the flow feed bypass of the gas increases due to a segregated gas flow pattern. This is critical considering that under industrial conditions, sulfur-containing hydrocarbons may have fractions of up to 75% in the gas phase. Therefore, the gas rate should be kept low in order to limit the degree to which it bypasses the liquid. On the other hand, from micro-packed-bed experiments at low gas flow rates it was shown that gas and liquid move through the column together, and evaporation and condensation did not affect the residence time of the component of interest, it being prudent to perform the kinetic experiments at lower gas-to-liquid flow ratios than those typically employed in TBRs (0.06 to 0.1).
