To find out the Radius of a Concave Surface (Metrology)

9.14.
(i) When the edges are well-defined.
(ii) When the edges are rounded up.
(i) When the edges are well-defined. This method is applicable to those parts which have large radius to curvature. This requires the use of a surface plate, angle plate, height gauge, depth micrometer, slip gauges and a C-clamp.
The part to be tested is kept on a surface plate and with the help of a depth micrometer the maximum depth of the cavity is determined. Let it be h. Next the part is kept iri such a way that cavity is resting against an angle plate and the part is then clamped in this position. The hole is then measured from edge to edge with a height gauge having a sharp scribing arm. Let the maximum reading, i.e. diameter of the hole be d (Fig. 9.15).
Let O be the assumed centre of the cavity and R the radius of curvature.

Fig. 9.15
(ii) When the edges are rounded up. When the edges of the cavity are rounded up, then the radius of curvature can be measured by a depth micrometer and slip gauges. The width of the depth micrometer base is measured with the help of slip gauges. Let it be d. Then it is placed in the cavity till it fully rests in the cavity, its frame touching all the sides of cavity (Fig. 9.16). The measuring tip is then lowered down till it touches the base. The reading is then noted on the thimble and let it be h. Now the case is similar to previous one and the radius of curvature R can be found out by the same formula.

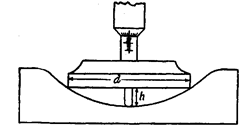
Fig. 9.16

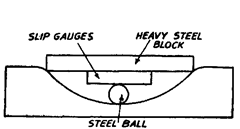
Fig. 9.17
Other method to note down d and h is by using a heavy steel block, a steel ball and slip gauges as shown in Fig. 9.17. In this method, the steel ball is placed in the cavity and the heavy steel block also put into the cavity. The space between the block and ball is filled up by a suitable length of slip gauges so that block is just touching the sides of cavity.
Here length of block is d and length of slip gauges and diameter of ball constitute h. The formula for finding the radius of curvature remains the same.