19.20.
If an event is sure to occur it has a probability of one. An event that is certain not to occur has a probability of zero. All other probabilities fall between these extremes of zero and one.
If in a system, an event has the probability of occurrence = pi and some other event has probability of occurrence = p2, then probability of either of two (p) is the sum or two probabilities i.e. p =pi+ p2. This is called the theorem of addition.
If the probability of an event in a system ispi and of some other event in other system is p2, then the probability (p) of both to occur simultaneously is product of two, i.e., p = pi x p2. This is called the theorem of multiplication.
The probability of occurrence of an event can be calculated by Binomial system or by Poisson Probability method. In the sampling inspection the following notations are used :
N = lot size, n = sample size,
c = acceptance number, p = %age defective.
The probability of zero defectives in sample = e~np
Probability of 1 defective = npe~np
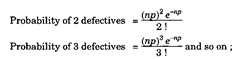
But for finding the probability of occurrence of any number of defectives corresponding to np and acceptance number is directly tabulated. (Refer Table 19.9).
Example 19.25.
(a) What are the rules of combining probabilities ?
(b) What do you understand by permutation ?
(c) What do you understand by combination ?
Solution,
(a) 1. The probability of an event A, denoted by P[A], is a number between 0 and 1 inclusive, an impossible event having probability 0 and one that is certain to occur having probability 1.
2. The probability that at least one of two events A and B occurs is given by
P[A + B}= P[A] + P[B] -P[AB] …(1)
3. The probability of the simultaneous occurrence of both A and B is given by
P[AB] = P[A]P[B/A] = P[B]P[AJB] …(2)
If the two events A and B are mutually exclusive (meaning that it is impossible for both to occur together), P[AB] = 0, then Eq. (1) becomes
P[A + B] = P[A] + P[B] …(3)
This is called the additional theorem for probabilities and is the reason for the use of + sign to denote “and/or” which when A and B are mutually exclusive, reduces to strict alternate “either-or”
Since the events A and A are mutually exclusive and one of these must occur therefore, PEA] + P[A] = 1 …(4)
The events A and 13 are said to be independents the probability of occurrence of A is the same whether B occurs or not, that is, if,
P\AIB] = P[AIB\ Now P[A] = P[AB] + P[AB]
= P[B]P[A/B] + P[B]P\A/B] from Eq. (1) If PIA/B] = PIA/B], this becomes
PEA] = P[A/B] (P[B] + P[B\) = P[A/B] and therefore, Eq. (2) can be written for independent events,
P[AB] = PEAJPES] …(5)
This is called Multiplication theorem for probabilities and is the reason for using AB to mean “A and B”. These theorems can be generalised to any number of events.
(b) A permutation of a finite number of distinguishable objects is any of their arrangements in a definite order. For example with n objects, by considering that the first place in the ordered arrangement can be filled in n ways, since any one of the n objects can be chosen. The next place can be filled in n – 1 ways, since only n – 1 objects are left to be picked. Similarly the third place can be filled in n – 2 ways, and so on until the last place can be filled in only one way, with the last object left. The total number of ways is therefore,
n(n-lXn-2X*-3)……(3X2X1)
and this number is denoted by n ! or An (read as “n factorial”). If the problem is to select r objects out of n distinguishable objects, and arranging them in order, then
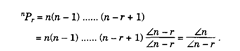
(c) A combination is the number of ways in which a certain number of articles are selected from a collection, note caring in what order they are arranged. The number of ways of picking out r objects from n distinguishable objects, called the number of combinations ofn things taken r at a time, will be denoted by nCr and is given by
![]()
