1.4.
Measuring Instruments are measuring devices that transform the measured quantity or a
related quantity into an indication or information.
Measuring instruments can either indicate directly the value of the measured quantity or
only indicate its equality to a known measure of the same quantity (e.g. equal arm balance, or null
detecting galvanometer). They may also indicate the value of the small difference between the
measured quantity and the measure having a value very near to it (comparator).
Measuring instruments usually utilise a measuring sequence in which the measured
quantity is transformed into a quantity perceptible to the observer (length, angle, sound, luminous
contrast).
Measuring instruments may be used in conjunction with separate material measures (e.g.
balances using standard masses to compare unknown mass), or they may contain internal parts to
reproduce the unit (like graduated rules, a precision thread, etc.)
1.4.1.
Measuring range.
It is the range of values of the measured quantity for which the
error obtained from a single measurement under normal conditions of use does not exceed the
maximum permissible error.
The measuring range is limited by the maximum capacity and the minimum capacity.
Maximum capacity is the upper limit of the measuring range and is dictated by the design
considerations or by safety requirements or both.
Minimum capacity is the lower limit of the measuring range. It is usually dictated by
accuracy requirements. For small values of the measured quantity in the vicinity of zero, the relative
error can be considerable even if the absolute error is small.
The measuring range may or may not coincide with the range of scale indication.
1.4.2.
Sensitivity
. It is the quotient of the increase in observed variable (indicated by pointer
and scale) and the corresponding increase in the measured quantity.
It is also equal to the length of any scale division divided by the value of that division
expressed in terms of the measured quantity.
The sensitivity may be constant or variable along the scale. In the first case, we get linear
transmission and in the second case, we get a non-linear transmission.
1.4.3.
Scale Interval.
It is the difference between two successive scale marks in units of the
measured quantity. (In the case of numerical indication, it is the difference between two consecutive
numbers).
The scale interval is an important parameter that determines the ability of the instrument
to give accurate indication of the value of the measured quantity.
The scale spacing, or the length of scale interval, should be convenient, for estimation of
fractions.
1.4.4.
Discrimination.
It is the ability of the measuring instrument to react to small changes
of the measured quantity.
1.4.5.
Hysteresis.
It is the difference between the indications of a measuring instrument
when the same value of the measured quantity is reached by increasing or by decreasing that
quantity.
The phenomenon of hysteresis is due to the presence of dry friction as well as to the properties
of elastic elements. It results in the loading and unloading curves of the instrument being separated
by a difference called the hysteresis error. It also results in the pointer not returning completely to
zero when the load is removed.
Hysteresis is particularly noted in instruments having elastic elements. The phenomenon
of hysteresis in materials is due mainly to the presence of internal stresses. It can be reduced
considerably by proper heat treatment.
1.4.6.
Response time.
It is the time which elapses after a sudden change in the measured
quantity until the instrument gives an indica-
tion differing from the true value by an amount
less than a given permissible error.
The curve showing the change of indica-
tion of an instrument due to sudden change of
measured quantity can take different forms
according to the relation between capacitances
that have to be filled, inertia elements and
damping elements.
When inertia elements are small enough
to be negligible, we get first order response
which is due to filling the capacitances in the
system through finite channels. The curve of
change of indication with time in that case is an
exponential curve. (Refer Fig. 1.1)
If the inertia forces are not negligible, we get second order response. There are three
possi-bilities of response (Refer Fig. 1.2.) according to the ratio of damping and inertia forces as
follows:
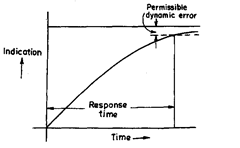
Fig. 1.1. First order response of an instrument.
— overdamped system—
where the final indica-
tion is approached
exponentially from one
side.
— under-damped system
—where the pointer ap-
proaches the position
corresponding to final
reading, passes it and
makes a number of os-
cillations around it
before it stops.
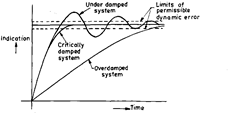
Fig. 1.2. Second order response of an instrument.
— critically damped system—where the pointer motion is aperiodic but quicker than in the
case of overdamped system.
In all these cases the response time is determined by the inter-section of one (or two) lines
surrounding the final indication line at a distance equal to the permissible value of dynamic error
with the response curve of the instrument.
1.4.7.
Repeatability.
It is the ability of the measuring instrument to give the same value
every time the measurement of a given quantity is repeated.
Any measurement process effected using a given instrument and method of measurement
is subject to a large number of sources of variation like environmental changes, variability in
operator performance and in instrument parameters. The repeatability is charactersied by the
dispersion of indications when the same quantity is repeatedly measured. The dispersion is
described by two limiting values or by the standard deviation.
The conditions under which repeatability is tested have to be specified.
1.4.8.
Bias.
It is the characteristic of a measure or a measuring instrument to give indications
of the value of a measured quantity whose average differs from the true value of that quantity.
Bias error is due to the algebraic summation of all the systematic errors affecting the
indication of the instrument. Sources of bias are maladjustment of the instrument, permanent set,
non-linearly errors, errors of material measures etc.
1.4.9.
Inaccuracy.
It is the total error of a measure or measuring instrument under specified
conditions of use and including bias and repeatability errors.
Inaccuracy is specified by two limiting values obtained by adding and subtracting to the bias
error the limiting value of the repeatability error.
If the known systematic errors are corrected, the remaining inaccuracy is due to the random
errors and the residual systematic errors that also have a random character.
This inaccuracy is called the “uncertainty of measurement”.
1.4.10.
Accuracy Class.
Measuring instruments are classified into accuracy classes accord-
ing to their metrological properties. There are two methods used in practice for classifying
instruments into accuracy classes.
1. The accuracy class may be expressed simply by a class ordinal number that gives an idea
but no direct indication of the accuracy (e.g. block gauges of accuracy class, 0,1, 2 etc.).
2. The accuracy class is expressed by a number stating the maximum permissible inaccuracy
as %age of the highest indication given by the instrument (e.g. an instrument of accuracy class 0.2
and maximum capacity 0—100 will have a maximum permissible inaccuracy of ± 0.2 at any point
in the scale of instrument.
1.4.11.
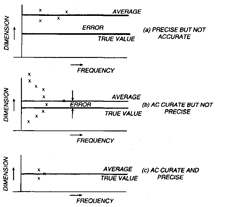
Precision and Accuracy.
Both these terms are associated with the measuring
that both use the accurate scales in accordance with the standard scales. In this case, accuracy of
the scale is important and it should be manufactured such that its units are in accordance with the
standard units set.
The distinction between the precision and accuracy will become clear by the following
example (shown in Fig. 1.3), in which several measurements are made on a component by different
types of instruments and results plotted.
From Fig. 1.3, it will be obvious that precision is concerned with a process or a set of
measurements, and not a single measurement. In any set of measurements, the individual
measurements are scattered about the mean, and the precision tells us to how well the various
measurements performed by same instrument on the same component agree with each other. It
will be appreciated that poor repeatability is a sure sign of poor accuracy. Good repeatability of the
instrument is a necessary but not a sufficient condition of good accuracy. Accuracy can be found by
taking root mean square of repeatability and systematic error i.e.
![]()
Error is the difference between the mean of set of readings on same component and the true
value. Less is the error, more accurate is the instrument. Since the true value is never known,
uncertainty creeps in, and the magnitude of error must be estimated by other means. The estimate
of uncertainty of a measuring process can be made by taking care of systematic and constant errors,
and other contributions to the uncertainty due to scatter of the results about the mean.
So wherever great precision is required in manufacture of mating components, they are
manufactured in a single plant, where measurements are taken with same standards and internal
measuring precision can achieve the desired results. If they are to be manufactured in different
plants and subsequently assembled in another, the accuracy of the measurement of two plants with
true standard value is important.
1.4.12.
Accuracy.
In mechanical inspection, the accuracy of measurement is the most
important aspect. The accuracy of an instrument is its ability to give correct results. It is, therefore,
better to understand the various factors which affect it and which are affected by it. The accuracy
of measurement to some extent is also dependent upon the sense of hearing or sense of touch or
sense of sight, e.g., in certain instrument the proportions of sub-divisions have to be estimated by
the sense of sight; of course, in certain instances the vernier device may be employed in order to
substitute the ‘estimation of proportion’ by ‘recognition of coincidence’. In certain instruments,
accuracy of reading depends upon the recognition of a threshold effect, i.e. whether the pointer is
“just moving, or ‘just not moving”.
One thing is very certain that there is nothing like absolute or perfect accuracy and there is
no instrument capable of telling us, whether or not we have got it. The phrases like ‘dead accurate’
or ‘dead right’ become meaningless and of only relative value. In other words, no measurement can
be absolutely correct ; and there is always some error, the amount of which depends upon the
accuracy and design of the measuring equipment employed and the skill of the operator using it,
and upon the method adopted for the measurement. In some instruments, accuracy depends upon
the recognition of a threshold effect. In some instruments, proportions of sub-divisions have to be
estimated. In such cases, skill of operator is responsible for accuracy, Parallax is also very common
and can be taken care of by installing a mirror below the pointer. How method of measurement
affect accuracy would be realised in angle measurement by sine bar, i.e. large errors may occur
when sine bar is intended to be used for measuring large angles. Apparatus and methods should
be designed so that errors in the final results are small compared with errors in actual measure-
ments made. The equipment chosen for a particular measurement must bear some relation to the
desired accuracy in the result, and as a general rule, an instrument which can be read to the next
decimal place beyond that required in the measurement should be used, i.e., if a measurement is
desired to an accuracy of 0.01 mm, then instrument with accuracy of 0.001 mm should be used for
this purpose.
When attempts are made to achieve higher accuracy in the measuring instruments, they
become increasingly sensitive. But an instrument can’t be more accurate than is permitted by degree
of sensitiveness, the sensitivity being defined as the ratio of the change of instrument indication to
the change of quantity being measured. It may be realized that the degree of sensitivity of an
instrument is not necessarily the same all over the range of its readings. Another important
consideration for achieving higher accuracy is that the readings obtained for a given quantity should
be same all the time, i.e. in other words the readings should be consistent. A highly sensitive
instrument is not necessarily consistent in its readings and, clearly, an inconsistent instrument
can’t be accurate to a degree better than its inconsistency. It may also be remembered that the
range of measurement usually decreases as the magnification increases and the instrument may
be more affected by temperature variations and be more dependent upon skill in use.
Thus, it is true to say that a highly accurate instrument possesses both greater sensitivity
and consistency. But at the same time an instrument which is sensitive and consistent need not
necessarily be accurate because the standard from which its scale is calibrated may be wrong. (It
is, of course, presupposed that there always exists an instrument whose accuracy is greater than
the one with which we are concerned). In such an instrument, the errors will be constant at any
given reading and therefore, it would be quite possible to calibrate it.
It is very obvious that higher accuracy can be achieved by incorporating the magnifying
devices in the instrument, and these magnifying devices carry with them their own inaccuracies,
e.g., in an optical system the lens system may distort the ray in a variety of ways and the success
of the system depends upon the fidelity with which the lens system can produce the magnified
images etc. In mechanical system the errors are introduced due to bending of levers, backlash at
the pivots, inertia of the moving parts, errors of the threads of screws etc. Probably the wrong
geometric design may also introduce errors. By taking many precautions we can make these errors
extremely small, but, the smaller we try to make them, the greater becomes the complication of our
task, and with this increased complication, the greater the number of possible sources of error which
we must take care_of. Thus the greater the accuracy is aimed at, greater the number of sources of
errors to be investigated and controlled. As regards the instrumental errors, they can be kept as
small as possible. The constant or knowable sources of errors can be determined by the aid of
superior instruments and the instrument may be calibrated accordingly. The variable or un-
knowable sources of errors make the true value lie within plus or minus departure from the observed
value and can’t be tied down more closely than that. However, an accurate measuring instrument
should fulfil the following requirements :
(i) It should possess the requisite and constant accuracy.
(ii) As far as possible, the errors should be capable of elimination by adjustment contained
within the instrument itself.
(iii) Every important source of inaccuracy should be known.
(iv) When an error can’t be eliminated, it should be made as small as possible.
(v) When an error can’t be eliminated, it should be capable of measurement by the instru-
ment itself and the instrument calibrated accordingly.
(vi) As far as possible the principle of similarity must be followed, i.e. the quantity to be
measured must be similar to that used for calibrating the instrument. Further the measuring
operations performed on the standard and on the unknown must be as identical as feasible and
under the same physical conditions (environment temperature, etc. and using the same procedures
in all respects in both the cases of calibration and measurement).
In some instruments, accuracy is expressed as percentage of full scale deflection, i.e.
percentage of maximum reading of instrument. Thus at lower readings in the range, accuracy may
be very poor. The range of such instruments should be selected properly so that the measured value
is at about 70-90% of the full range.
Accuracy in measurement is essential at all stages of product development from research to
development and design, production, testing and evaluation, quality assurance, standardisation,
on-line control, operational performance appraisal, reliability estimation, etc.
The last word in connection with accuracy is that the accuracy at which we aim, that is to
say, the trouble we take to avoid errors in manufacture and in measuring those errors during
inspection must depend upon the job itself and on the nature of what is required, i.e. we should
make ourselves very sure whether we want that much accuracy and that cost to achieve it will be
compensated by the purpose for which it is desired.
1.4.13.
Accuracy and Cost
. The basic objective of metrology should be to provide the
accuracy required at the most economical cost. The accuracy of measuring system includes elements
such as :
(a) Calibration Standards,
(b) Workpiece being measured,
(c) Measuring Instruments
(d) Person or Inspector carrying out the measurement, and
(c) Environmental influences.
The above arrangement and analysis of the five basic Metrology elements can be composed
into the acronym SWIPE for convenient reference :
S = Standard, W = Workpiece, / = Instrument, P = Person and E = Environment.
Higher accuracy can be achieved only if, all the sources of errors due to the above five
elements in the measuring system be analysed and steps taken to eliminate them. An attempt is
made here to summarise the various factors affecting these five elements.
1. Standard.lt may be affected by ambient influences (thermal expansion), stability with
time, elastic properties, geometric compatibility, and position of use.
2. Workpiece, itself may be affected by ambient influences, cleanliness, surface condition,
elastic properties, geometric truth, arrangement of supporting it, provision of defining datum etc.
3. Instrument may be affected by hysteresis, backlash, friction, zero drift error, deformation
in handling or use of heavy workpieces, inadequate amplification, errors in amplification device,
calibration errors, standard errors, correctness of geometrical relationship of workpiece and
standard, proper functioning of contact pressure control, mechanical parts (slides, ways, or moving
elements) working efficiently, and repeatability adequacy etc.
4. Personal errors can be many and mainly due to improper training in use and handling,
skill, sense of precision and accuracy appreciation, proper selection of instrument, attitude towards
and realisation of personal accuracy achievements, etc.
5. Environment exerts a great influence. It may be affected by temperature ; thermal
expansion effects due to heat radiation from light, heating of components by sunlight and people,
temperature equalisation of work, instrument and standard ; surroundings; vibrations ; lighting;
pressure gradients (affect optical measuring systems) etc.
The design of measuring systems involves proper
analysis of cost-to-accuracy consideration and the general
characteristics of cost and accuracy appears to be as shown
in Fig. 1.4.
It will be clear from the graph that the cost rises
exponentially with accuracy. If the measured quantity re-
lates to a tolerance (i.e. the permissible variation in the
measured quantity), the accuracy objective should be 10%
or slightly less of the tolerance. In a few cases, because of
technological limitations, the accuracy may be 20% of the
tolerance ; because demanding too high accuracy may tend
to make the measurement unreliable. In practice, the
desired ratio of accuracy to tolerance is decided by consider-
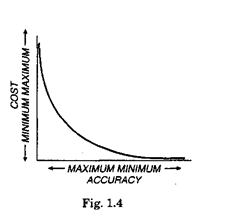
ing the factors such as the cost of measurement versus quality and the reliability criterion of the
product.
1.4.14.
Magnification.
The human limitations or incapability to read instruments places
limit on sensitiveness of instruments. Magnification (or amplification) of the signal from measuring
instrument can make it better readable. The magnification is possible on mechanical, pneumatic,
optical, electrical principles or combinations of these.
Magnification by mechanical means is the simplest and costwise most economical method.
The various methods of mechanical magnification are based on the principles of lever, wedge, gear
train etc.
In the case of magnification by wedge method, magnification is equal to tan 8, where 6 is the
angle of wedge.
Mechanical magnification method is usually grouped with other type of magnification
methods to combine their merits.
Optical magnification is based on the principle of reflection by tilting a mirror, or on
projection technique. In the case of reflection by a mirror, the angular magnification is 2 because
the reflected ray is tilted by twice the angle of tilt of mirror. With 2-mirror system four-fold
magnification is obtained.
In the case of optical lever magnification, various features of the test specimen are estab-
lished on projector screen using reference lines as datum. Very high magnifications are possible in
such systems.
Pneumatic magnification method is ideally suited for internal measurement. It offers better
reliability and stability. Very high magnifications (upto 30,000 :1) are possible.
Electrical magnification methods have the advantages of better control on the amount of
magnification, quick response, large range of linearity, etc. Electrical magnification is based on
sensing change in inductance or capacitance, which is measured by a wheatstone bridge.
Electronic method of magnification is more reliable and accurate. Electronic methods are
ideally suited for processing of signals, viz. amplification, filtering, validation of signal, sensing for
high and low limits, autocalibration, remote control telemetry etc.
1.4.15.
Repeatability.
Repeatability is the most important factory in any measuring system
as it is the characteristics of the measuring system whereby repeated trials of identical inputs of
measured value produce the same indicated output from the system.
It is defined as the ability of a measuring system to reproduce output readings when the
same measurand value is applied to it consecutively, under the same conditions, and in the same
direction. It could be expressed either as the maximum difference between output readings, or as
“within … per cent of full scale output.”
Repeatability is the only characteristic error which cannot be calibrated out of the measuring
system. Thus repeatability becomes the limiting factor in the calibration process, thereby limiting
the overall measurement accuracy. In effect, repeatability is the minimum uncertainty in the
comparison between measurand and reference.
1.4.16.
Uncertainty.
It is the range about the measured value within which the true value
of the measured quantity is likely to lie at the stated level of confidence. It can be calculated when
the trade or population standard deviation is known or it can be estimated from the standard
deviation calculated from finite number of observation having normal distribution.
1.4.17.
Confidence levels.
It is the measure of a degree of reliability with which the results
of measurement can be expressed. Thus if u be uncertainty in a measured quantity x at 98%
confidence level, then the probability for true value to lie between x + u and x – u is 98%. Thus on
measuring this quantity a large number of times, then 98% of the values will lie in between x + u
and x – u.
1.4.18.
Calibration.
The calibration of any measuring system is very important to get
meaningful results. In case where the sensing system and measuring system are different, then it
is imperative to calibrate the system as an integrated whole in order to take into account the error
producing properties of each component. Calibration is usually carried out by making adjustments
such that readout device produces zero output for zero-measurand input, and similarly it should
display an output equivalent to the known measurand input near the full-scale input value.
It is important that any measuring system calibration should be performed under environ-
mental conditions that are as close as possible to those conditions under which actual measurements
are to be made.
It is also important that the reference measured input should be known to a much greater
degree of accuracy—usually the calibration standard for the system should be at least one order of
magnitude more accurate than the desired measurement system accuracy, i.e. accuracy ratio of
10: 1.
1.4.19.
Calibration vs. Certification
. Calibration is the process of checking the dimensions.
and tolerances of a gauge, or the accuracy of a measurement instrument by comparing it to a like
instrument/gauge that has been certified as a standard of known accuracy. Calibration is done by
detecting and adjusting any discrepancies in the instrument’s accuracy to bring it within acceptable
limits. Calibration is done over a period of time, according to the usage of the instrument and the
materials of its parts. The dimensions and tolerances of the instrument/gauge are checked to
determine whether it has departed from the previously accepted certified condition. If departure is
within limits, corrections are made. If deterioration is to a point that requirements can’t be met any
more then the instrument/gauge can be downgraded and used as a rough check, or it may be
reworked and recertified, or be scrapped. If a gauge is used frequently, it will require more
maintenance and more frequent calibration.
Certification is performed prior to use of instrument/gauge and later to reverify if it has been
reworked so that it again meets its requirements. Certification is given by a comparison to a
reference standard whose calibration is traceable to an accepted national standard. Further such
reference standards must have been certified and calibrated as master not more than six months
prior to use.
1.4.20.
Sensitivity and Readability.
The terms “sensitivity” and “readability” are often
confused with accuracy and precision. Sensitivity and readability are primarily associated with
equipment while precision and accuracy are associated with the measuring process. It is not
necessary that the most sensitive or the most readable equipment will give most precise or the most
accurate results.
Sensitivity refers to the ability of a measuring device to detect small differences in a quantity
being measured. It may so happen that high sensitivity instrument may lead to drifts due to thermal
or other effects, so that its indications may be less repeatable or less precise than those of the
instrument of lower sensitivity.
Readability refers to the susceptibility of a measuring device to having its indications
converted to a meaningful number. A micrometer instrument can be made more readable by using
verniers. Very finely spaced lines may make a scale more readable when a microscope is used, but
for the unaided eye, the readability is poor.
1.4.21.
Uncertainty in Measurement.
Whenever a value of physical quantity is deter-
mined through a measurement process, some errors are inherent in the process of measurement
and it is only the best estimate value of the physical quantity obtained from the given experimental
data. Thus quantifying a measurable quantity through any measurement process is meaningful
only if the value of the quantity measured with a proper unit of measurement is accompanied by
an overall uncertainty of measurement. It has two components arising due to random errors and
systematic errors. Uncertainty in measurement could be defined as that part of the expression of
the result of a measurement which states the range of values within which the true value, or if
appropriate, the conventional true value is estimated to lie. In cases where there is adequate
information based on a statistical distribution, the estimate may be associated with a specified
probability. In other cases, an alternative form of numerical expression of the degree of confidence
to be attached to the estimate may be given.
1.4.22.
Random uncertainty and Systematic uncertainty.
Random uncertainty is that
part of uncertainty in assigning the value of a measured quantity which is due to random errors.
The value of the random uncertainty is obtained on multiplication of a measure of the random errors
which is normally the standard deviation by a certain factor t\ The factor’t’ depends upon the
sample size and the confidence level. Systematic uncertainty is that part of uncertainty which is
due to systematic errors and cannot be experimentally determined unless the equipment and
environmental conditions are changed. It is obtained by suitable combination of all systematic errors
arising due to different components of the measuring system.
It is necessary to understand difference between systematic uncertainty and correction.
The calibration certificate of an instrument gives a correspondence between its indication
and the quantity it is most likely to measure. The difference between them is the correction which
is to be invariably applied. However, there will be an element of doubt in the value of the correction
so stated. This doubt is quantitatively expressed as accuracy or overall uncertainty in assigning
the value to the correction stated and will be one component of the systematic uncertainty of that
instrument. For example, in case of a metre bar, the distance between the zero and 1,000 mm
graduation marks may be given as 1000.025 ± 0.005 mm. Then 0.025 mm is the correction and 0.005
mm is the component of systematic uncertainty of the metre bar.
1.4.23.
Traceability.
This is the concept of establishing a valid calibration of a measuring
instrument or measurement standard by step-by-step comparison with better standards up to an
accepted or specified standard. In general, the concept of traceability implies eventual reference to
an appropriate national or international standard.
1.4.24.
Fiducial Value.
A prescribed value of a quantity to which reference is made, for
example, in order to define the value of an error as a proportion of this prescribed value.
