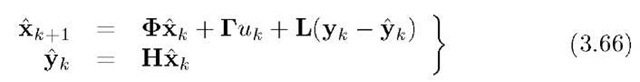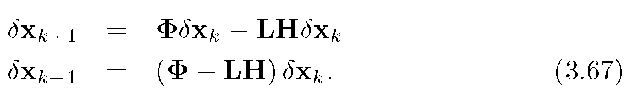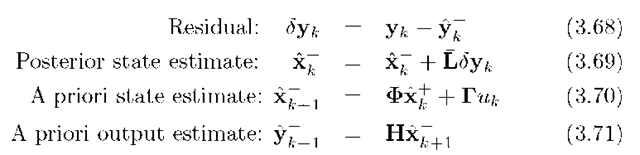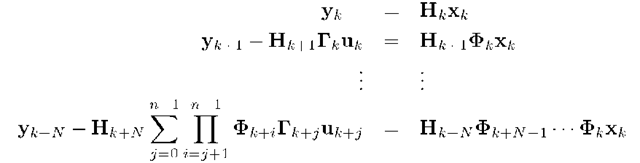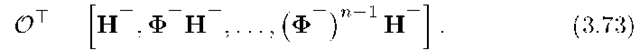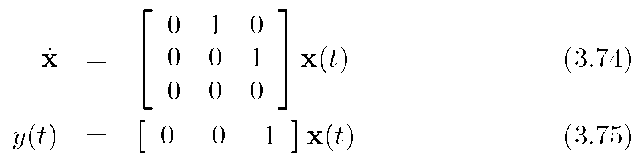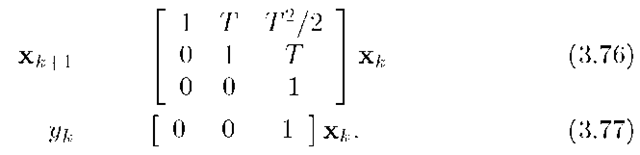The state space model format clearly shows that a system may have many internal variables (e.g., states) and fewer outputs (e.g., y). This is true for a variety of reasons including cost, power, or lack of appropriate sensors. If knowledge of the state vector is desired, but is not directly measured, then we have the problem referred to as state estimation. State estimation is useful in control applications, when a few outputs are available, but knowledge of the system state would allow higher performance control. It is also true in navigation systems, where several error variables are of interest, but few external measurements (e.g., ranges or velocities) are available. When it is advantageous to know the internal state, the question arises of how to estimate the state from the available outputs.
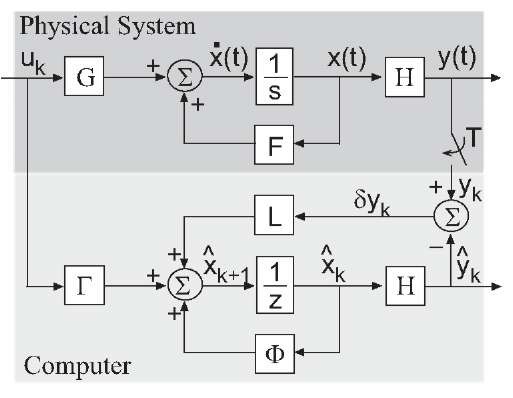
Figure 3.4: State estimator implementation for the continuous-time physical system of eqn. (3.15) with the output sampled every T seconds and the input u(t) constant over each sampling interval.
This section presents the problem of state estimation for deterministic systems from a stability point of view.
For a discrete-time system described via eqn. (3.39-3.40), consider the following approach:
where![]() is an estimate of the state
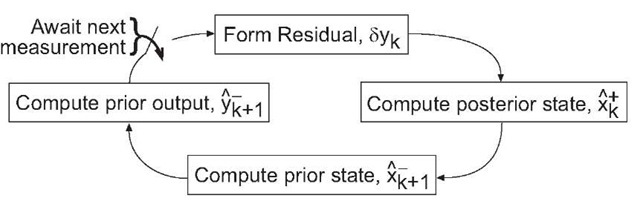
is an estimate of the state![]() at the fc-th instant of time and L is a design parameter referred to as the estimator gain vector. Figure 3.4 depicts the actual system and the state estimator where the symbol z represents a time-advance and Z represents a time-delay. The figure shows that the state of the physical system evolves in continuous time and is not directly measurable. Instead, output y is measured at discrete-time instants
at the fc-th instant of time and L is a design parameter referred to as the estimator gain vector. Figure 3.4 depicts the actual system and the state estimator where the symbol z represents a time-advance and Z represents a time-delay. The figure shows that the state of the physical system evolves in continuous time and is not directly measurable. Instead, output y is measured at discrete-time instants![]() From the discrete-time measurements of the output,eqn. (3.66) is implemented on the application computer to estimate the state vector. Because the state estimator is implemented computationally, the state estimates are conveniently available on the computer for use by control, planning, or other tasks as deemed appropriate by the designer.
From the discrete-time measurements of the output,eqn. (3.66) is implemented on the application computer to estimate the state vector. Because the state estimator is implemented computationally, the state estimates are conveniently available on the computer for use by control, planning, or other tasks as deemed appropriate by the designer.
For analysis, we form the difference equation for the state estimation error![]() by subtracting eqn. (3.66) from eqn. (3.39) to obtain
by subtracting eqn. (3.66) from eqn. (3.39) to obtain
If the state estimation error is to converge to zero, then eqn. (3.67) must be asymptotically stable. Eqn. (3.67) will be asymptotically (actually exponentially) stable if the eigenvalues of![]() have magnitude less than one.
have magnitude less than one.
The above analysis is meant to motivate the idea of state estimation (also called state observation). Several questions remain unanswered. The above analysis has tacitly assumed that it is possible to choose the matrix L so that the eigenvalues of![]() have magnitude less than one. This may not always be possible. This issue is related to the question of when the system state can be estimated from a given set of measurements. This issue is discussed in Section 3.6.1. Once it is determined that state estimation is possible for a given system, it is natural to consider whether it is possible to derive an optimal state estimator relative to a given optimality criteria. The above analysis also only discusses time-invariant systems. The time-varying case is more complex and will only be discussed in the context of optimal estimation.
have magnitude less than one. This may not always be possible. This issue is related to the question of when the system state can be estimated from a given set of measurements. This issue is discussed in Section 3.6.1. Once it is determined that state estimation is possible for a given system, it is natural to consider whether it is possible to derive an optimal state estimator relative to a given optimality criteria. The above analysis also only discusses time-invariant systems. The time-varying case is more complex and will only be discussed in the context of optimal estimation.
Note that the resulting state estimation algorithm is recursive in nature and can be split into two parts: a measurement update and a time update. At fc-th time step prior to using![]() we have
we have![]() The computation for the fc-th time step proceeds as follows:
The computation for the fc-th time step proceeds as follows:
where![]() This ordering of the operations is depicted in Figure 3.5. Eqn. (3.68) computes the measurement residual. Eqn. (3.69) can be thought of as a blending of all past measurement information propagated to the present time (as represented by
This ordering of the operations is depicted in Figure 3.5. Eqn. (3.68) computes the measurement residual. Eqn. (3.69) can be thought of as a blending of all past measurement information propagated to the present time (as represented by![]() with the new information available from the current measurement (as represented by the residual
with the new information available from the current measurement (as represented by the residual![]() While
While![]() represents the estimate of
represents the estimate of![]() using all measurements up to but not including
using all measurements up to but not including![]() the vector
the vector![]() represents the estimate of
represents the estimate of![]() after incorporating all measurements including
after incorporating all measurements including![]() Performing the operations in this order minimizes the computation (i.e., delay) between the arrival of
Performing the operations in this order minimizes the computation (i.e., delay) between the arrival of![]() and the availability of
and the availability of![]() for use in control (e.g., calculation of
for use in control (e.g., calculation of![]() ), navigation, and planning computations. After those computations are complete, but prior to the arrival of the next measurement, eqns. (3.70-3.71) perform the time propagation necessary to prepare the data for the (k + 1)-th measurement.
), navigation, and planning computations. After those computations are complete, but prior to the arrival of the next measurement, eqns. (3.70-3.71) perform the time propagation necessary to prepare the data for the (k + 1)-th measurement.
Figure 3.5: State estimator implementation organized to minimize delay between arrival of![]() and computation of
and computation of![]()
A critical question is proper definition of the state of the system containing the plant and the state estimator. The following variables are open for consideration:![]() A first thought might be to combine all three into a vector of length 3n; however, this is not a minimal state definition because the three vectors are linearly dependent according to the equation
A first thought might be to combine all three into a vector of length 3n; however, this is not a minimal state definition because the three vectors are linearly dependent according to the equation ![]() Knowledge of any two of the three vectors allows calculation of the third. The dimension of system containing both the plant and the state estimator is
Knowledge of any two of the three vectors allows calculation of the third. The dimension of system containing both the plant and the state estimator is![]() Three valid state vectors are:
Three valid state vectors are:![]()
The question of whether the plant state can be estimated is addressed in Subsection 3.6.1. The question of how to select the gain L to achieve a stable estimator design is addressed in Subsection 3.6.2. For a linear deterministic system, the state estimator design and analysis work with eqn. (3.67) and performance is independent of the actual state and control signal.
Observability
The previous section introduced the idea of estimation of the system state from the available outputs. Prior to trying to design a state estimator, it is important to consider the question of whether the state can be estimated from the available outputs.
This section analyzes the state estimation problem using the inversion-based solution method discussed in Section B.4. It is important for the reader to note that this approach to examining when the state estimation problem is solvable is distinct from the actual method of designing the state estimator. In particular, the vector Z defined below will never actually be computed directly.
Consider the problem of estimating the state![]() of the system described by eqn. (3.44) from the sequence of outputsFor this system, using eqns. (3.45-3.46),
of the system described by eqn. (3.44) from the sequence of outputsFor this system, using eqns. (3.45-3.46),
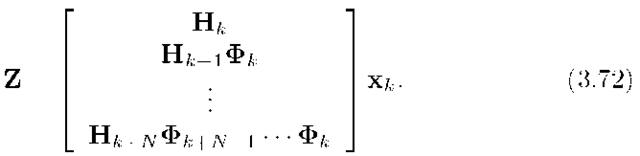
where all quantities in the left-hand side of the equation are known. The vector in the left-hand side will be denoted as Z. This set of equations can be written conveniently in matrix notation as
Therefore,![]() can be estimated from
can be estimated from![]() if the matrix on the right-hand side of eqn. (3.72) has rank equal to n (i.e., full column rank) for some N. For time-invariant systems this condition reduces to checking the rank of the matrix
if the matrix on the right-hand side of eqn. (3.72) has rank equal to n (i.e., full column rank) for some N. For time-invariant systems this condition reduces to checking the rank of the matrix
Example 3.14 Given the state space system
where![]() and only acceleration is being sensed. By the methods of Section 3.5.5, the equivalent discrete-time plant model is
and only acceleration is being sensed. By the methods of Section 3.5.5, the equivalent discrete-time plant model is
The observability matrix for this system is
which has rank one. This should match the reader’s intuition regarding this problem, since two constants of integration would be involved in determining position and velocity from acceleration. An accelerometer alone cannot determine these unknown constants. Even if the initial conditions were exactly known, errors in the acceleration measurement could not be detected or removed.
Example 3.15 Consider the same dynamic system as described by eqn. (3.74), but with position being measured instead of acceleration. In the system model, eqns. (3.74) and (3.76) would not change, but the output matrix would become![]() In this case, the observability matrix is
In this case, the observability matrix is
which has full column rank (for![]() ). Again, the mathematics verifies the intuition behind the problem, since at least three samples of position are required to estimate acceleration.
). Again, the mathematics verifies the intuition behind the problem, since at least three samples of position are required to estimate acceleration.
The above analysis shows that when the system state is observable it is possible to estimate the state in a minimum of N discrete-time steps; however, this is not usually done. Instead, computational issues, stability, and noise considerations usually motivate estimators which have guaranteed asymptotic convergence, as was discussed earlier in this section.