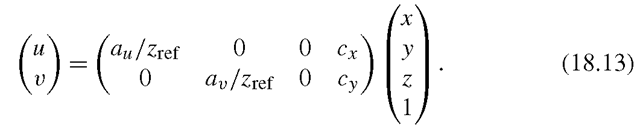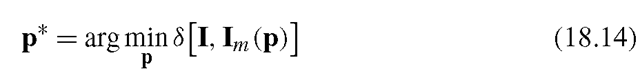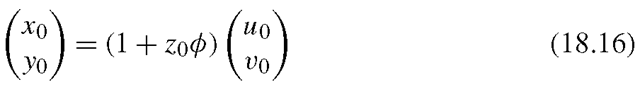Introduction
The problem of facial action tracking has been a subject of intensive research in the last decade. Mostly, this has been with such applications in mind as face animation, facial expression analysis, and human-computer interfaces. In order to create a face animation from video, that is, to capture the facial action (facial motion, facial expression) in a video stream, and then animate a face model (depicting the same or another face), a number of steps have to be performed. Naturally, the face has to be detected, and then some kind of model has to be fitted to the face. This can be done by aligning and deforming a 2D or 3D model to the image, or by localizing a number of facial landmarks. Commonly, these two are combined. The result must in either case be expressed as a set of parameters that the face model in the receiving end (the face model to be animated) can interpret.
Depending on the application, the model and its parameterization can be simple (e.g., just an oval shape) or complex (e.g., thousands of polygons in layers simulating bone and layers of skin and muscles). We usually wish to control appearance, structure, and motion of the model with a small number of parameters, chosen so as to best represent the variability likely to occur in the application. We discriminate here between rigid face/head tracking and tracking of facial action. The former is typically employed to robustly track the faces under large pose variations, using a rigid face/head model (that can be quite non-face specific, e.g., a cylinder). The latter here refers to tracking of facial action and facial features, such as lip and eyebrow motion. The treatment in this topic is limited to tracking of facial action (which, by necessity, includes the head tracking).
The parameterization can be dependent or independent on the model. Examples of model independent parameterizations are MPEG-4 Face Animation Parameters (see Sect. 18.2.3) and FACS Action Units (see Sect. 18.2.2). These parameteriza-tions can be implemented on virtually any face model, but leaves freedom to the model and its implementation regarding the final result of the animation. If the transmitting side wants to have full control of the result, more dense parameterizations (controlling the motion of every vertex in the receiving face model) are used. Such parameterizations can be implemented by MPEG-4 Facial Animation Tables (FAT), morph target coefficients, or simply by transmitting all vertex coordinates at each time step.
Then, the face and its landmark/features/deformations must be tracked through an image (video) sequence. Tracking of faces has received significant attention for quite some time but is still not a completely solved problem.
Previous Work
A plethora of face trackers are available in the literatures, and only a few of them can be mentioned here. They differ in how they model the face, how they track changes from one frame to the next, if and how changes in illumination and structure are handled, if they are susceptible to drift, and if real-time performance is possible. The presentation here is limited to monocular systems (in contrast to stereo-vision) and 3D tracking.
Rigid Face/Head Tracking
Malciu and Prêteux [36] used an ellipsoidal (alternatively an ad hoc Fourier synthesized) textured wireframe model and minimized the registration error and/or used the optical flow to estimate the 3D pose. LaCascia et al. [31] used a cylindrical face model with a parameterized texture being a linear combination of texture warping templates and orthogonal illumination templates. The 3D head pose was derived by registering the texture map captured from the new frame with the model texture. Stable tracking was achieved via regularized, weighted least-squares minimization of the registration error.
Basu et al. [7] used the Structure from Motion algorithm by Azerbayejani and Pentland [6] for 3D head tracking, refined and extended by Jebara and Pentland [26] and Strom [56] (see below). Later rigid head trackers include notably the works by Xiao et al. [64] and Morency et al. [40].
Facial Action Tracking
In the 1990s, there were many approaches to non-rigid face tracking. Li et al. [33] estimated face motion in a simple 3D model by a combination of prediction and a model-based least-squares solution to the optical flow constraint equation. A render-feedback loop was used to combat drift. Eisert and Girod [16] determined a set of animation parameters based on the MPEG-4 Facial Animation standard (see Sect. 18.2.3) from two successive video frames using a hierarchical optical flow based method. Tao et al. [58] derived the 3D head pose from 2D-to-3D feature correspondences. The tracking of nonrigid facial features such as the eyebrows and the mouth was achieved via a probabilistic network approach. Pighin et al. [50] derived the face position (rigid motion) and facial expression (nonrigid motion) using a continuous optimization technique. The face model was based on a set of 3D face models.
In this century, DeCarlo and Metaxas [11] used a sophisticated face model parameterized in a set of deformations. Rigid and nonrigid motion was tracked by integrating optical flow constraints and edge-based forces, thereby preventing drift. Wiles et al. [63] tracked a set of hyperpatches (i.e., representations of surface patches invariant to motion and changing lighting).
Gokturk et al. [22] developed a two-stage approach for 3D tracking of pose and deformations. The first stage learns the possible deformations of 3D faces by tracking stereo data. The second stage simultaneously tracks the pose and deformation of the face in the monocular image sequence using an optical flow formulation associated with the tracked features. A simple face model using 19 feature points was utilized.
As mentioned, Strom [56] used an Extended Kalman Filter (EKF) and Structure from Motion to follow the 3D rigid motion of the head. Ingemars and Ahlberg extended the tracker to include facial action [24]. Ingemars and Ahlberg combined two sparse texture models, based on the first frame and (dynamically) on the previous frame respectively, in order to get accurate tracking and no drift. Lefèvre and Odobez used a similar idea, but separated the texture models more, and used Nelder-Mead optimization [42] instead of an EKF (see Sect. 18.4).
As follow-ups to the introduction of Active Appearance Models, there were several appearance-based tracking approaches. Ahlberg and Forchheimer [4, 5] represented the face using a deformable wireframe model with a statistical texture. A simplified Active Appearance Model was used to minimize the registration error. Because the model allows deformation, rigid and non-rigid motions are tracked. Dornaika and Ahlberg [12, 14] extended the tracker with a step based on random sampling and consensus to improve the rigid 3D pose estimation. Fanelli and Fratar-cangeli [18] followed the same basic strategy, but exploited the Inverse Compositional Algorithm by Matthews and Baker [37]. Zhou et al. [65] and Dornaika and Davoine [15] combined appearance models with a particle filter for improved 3D pose estimation.
Outline
This topic explains the basics of parametric face models used for face and facial action tracking as well as fundamental strategies and methodologies for tracking. A few tracking algorithms serving as pedagogical examples are described in more detail. The topic is organized as follows: In Sect. 18.2 parametric face modeling is described. Various strategies for tracking are discussed in Sect. 18.3, and a few tracker examples are described in Sects. 18.4-18.6. In Sect. 18.6.3 some examples of commercially available tracking systems are give.
Parametric Face Modeling
There are many ways to parameterize and model the appearance and behavior of the human face. The choice depends on, among other things, the application, the available resources, and the display device. Statistical models for analyzing and synthesizing facial images provide a way to model the 2D appearance of a face. Here, other modeling techniques for different purposes are mentioned as well.
What all models have in common is that a compact representation (few parameters) describing a wide variety of facial images is desirable. The parameter sets can vary considerably depending on the variability being modeled. The many kinds of variability being modeled/parameterized include the following.
• Three-dimensional motion and pose—the dynamic, 3D position and rotation of the head. Nonrigid face/head tracking involves estimating these parameters for each frame in the video sequence.
• Facial action—facial feature motion such as lip and eyebrow motion. Estimated by nonrigid tracking.
• Shape and feature configuration—the shape of the head, face and the facial features (e.g., mouth, eyes). This could be estimated by some alignment or facial landmark localization methods.
• Illumination—the variability in appearance due to different lighting conditions.
• Texture and color—the image pattern describing the skin.
• Expression—muscular synthesis of emotions making the face look, for example, happy or sad.
For a head tracker, the purpose is typically to extract the 3D motion parameters and be invariant to all other parameters. Whereas, for example, a user interface being sensitive to the mood of the user would need a model extracting the expression parameters, and a recognition system should typically be invariant to all but the shape and texture parameters.
Eigenfaces
Statistical texture models in the form of eigenfaces [30, 53, 60] have been popular for facial image analysis. The basic idea is that a training set of facial images are collected and registered, each image is reshaped into a vector, and a principal component analysis (PCA) is performed on the training set. The principal components are called eigenfaces. A facial image (in vector form), x, can then be approximated by a linear combination, X, of these eigenfaces, that is,
where X is the average of the training set,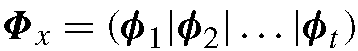
contains the eigenfaces, and
is a vector of weights or eigenface parameters. The parameters minimizing
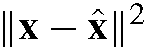are given by
Commonly, some kind of image normalization is performed prior to eigenface computation.
The space spanned by the eigenfaces is called the face subspace. Unfortunately, the manifold of facial images has a highly nonlinear structure and is thus not well modeled by a linear subspace. Linear and nonlinear techniques are available in the literature and often used for face recognition. For face tracking, it has been more popular to linearize the face manifold by warping the facial images to a standard pose and/or shape, thereby creating shape-free [10], geometrically normalized [55], or shape-normalized images and eigenfaces (texture templates, texture modes) that can be warped to any face shape or texture-mapped onto a wireframe face model.
Facial Action Coding System
During the 1960s and 1970s, a system for parameterizing minimal facial actions was developed by psychologists trying to analyze facial expressions. The system was called the Facial Action Coding System (FACS) [17] and describes each facial expression as a combination of around 50 Action Units (AUs). Each AU represents the activation of one facial muscle.
The FACS has been a popular tool not only for psychology studies but also for computerized facial modeling (an example is given in Sect. 18.2.5). There are also other models available in the literatures, for example, Park and Waters [49] described modeling skin and muscles in detail, which falls outside the scope of this topic.
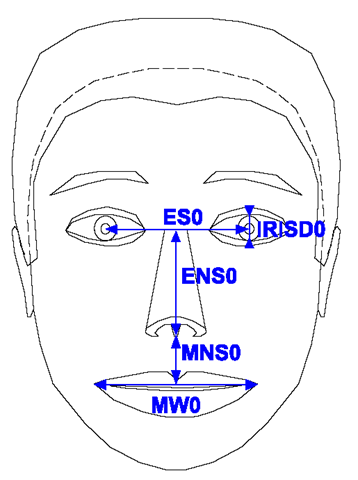
Fig. 18.1 Face Animation Parameter Units (FAPU)
MPEG-4 Facial Animation
MPEG-4, since 1999 an international standard for coding and representation of audiovisual objects, contains definitions of face model parameters [41, 47].
There are two sets of parameters: Facial Definition Parameters (FDPs), which describe the static appearance of the head, and Facial Animation Parameters (FAPs), which describe the dynamics.
MPEG-4 defines 66 low-level FAPs and two high-level FAPs. The low-level FAPs are based on the study of minimal facial actions and are closely related to muscle actions. They represent a complete set of basic facial actions, and therefore allow the representation of most natural facial expressions. Exaggerated values permit the definition of actions that are normally not possible for humans, but could be desirable for cartoon-like characters.
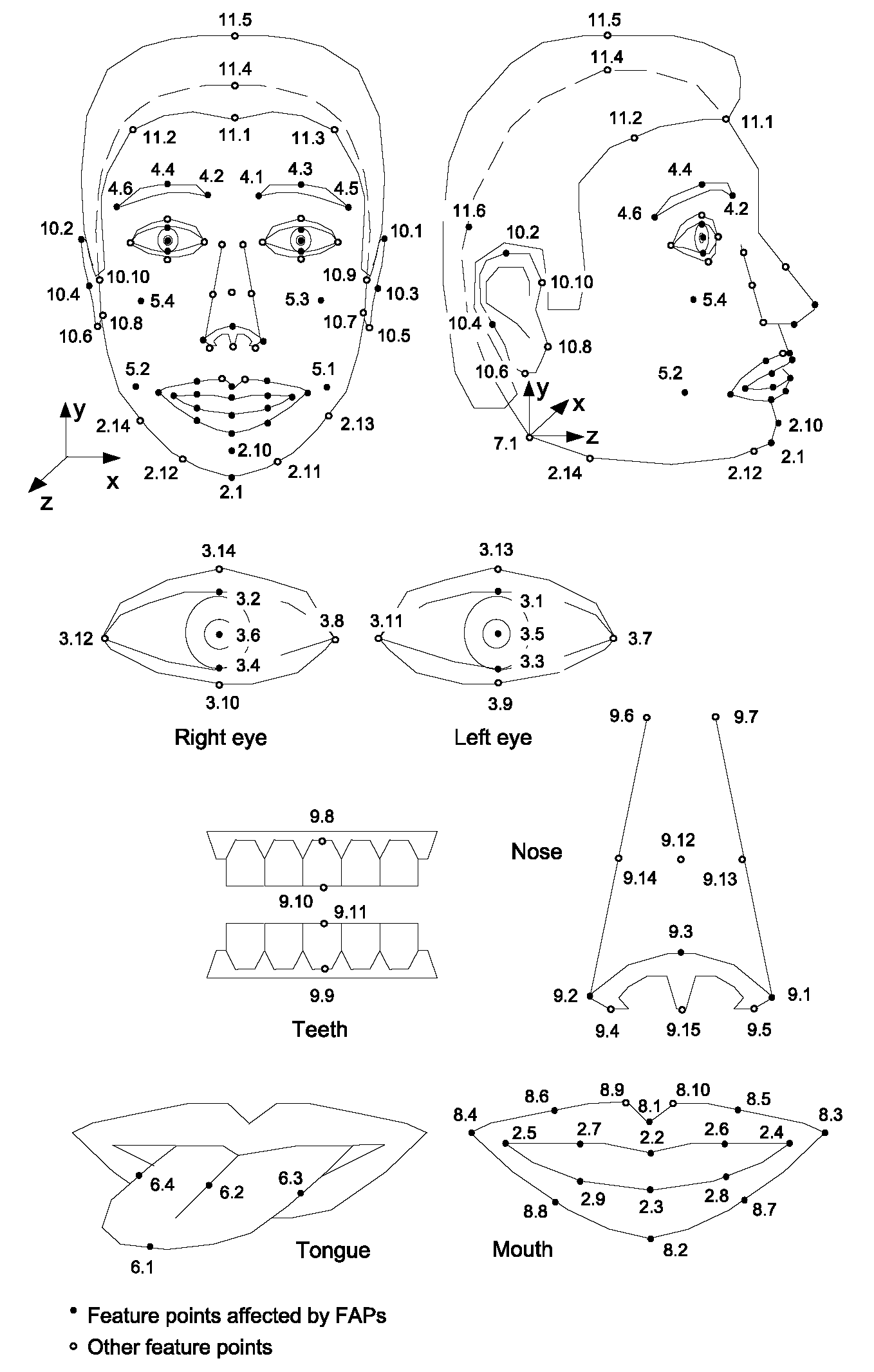
All low-level FAPs are expressed in terms of the Face Animation Parameter Units (FAPUs), illustrated in Fig. 18.1. These units are defined in order to allow interpretation of the FAPs on any face model in a consistent way, producing reasonable results in terms of expression and speech pronunciation. They correspond to distances between key facial features and are defined in terms of distances between the MPEG-4 facial Feature Points (FPs, see Fig. 18.2). For each FAP it is defined on which FP it acts, in which direction it moves, and which FAPU is used as the unit for its movement. For example, FAP no. 3, open_jaw, moves the Feature Point 2.1 (bottom of the chin) downwards and is expressed in MNS (mouth-nose separation) units. The MNS unit is defined as the distance between the nose and the mouth (see Fig. 18.1) divided by 1024. Therefore, in this example, a value of 512 for the FAP no. 3 means that the bottom of the chin moves down by half of the mouth-nose separation. The division by 1024 is introduced in order to have the units sufficiently small that FAPs can be represented in integer numbers.
The two high-level FAPs are expression and viseme. expression can contain two out of a predefined list of six basic expressions: joy, sadness, anger, fear, disgust and surprise. Intensity values allow to blend the two expressions. Similarly,viseme can contain two out of a predefined list of 14 visemes, and a blending factor to blend between them.
Fig. 18.2 Facial Feature Points (FP)
The neutral position of the face (when all FAPs are 0) is defined as follows:
• The coordinate system is right-handed; head axes are parallel to the world axes.
• Gaze is in the direction of Z axis.
• All face muscles are relaxed.
• Eyelids are tangent to the iris.
• The pupil is one third of IRISD0.
• Lips are in contact—the line of the lips is horizontal and at the same height of lip corners.
• The mouth is closed and the upper teeth touch the lower ones.
• The tongue is flat, horizontal with the tip of tongue touching the boundary between upper and lower teeth (feature point 6.1 touching 9.11, see Fig. 18.2).
All FAPs are expressed as displacements from the positions defined in the neutral face.
The FDPs describe the static shape of the face by the 3D coordinates of each feature point and the texture as an image with the corresponding texture coordinates.
Computer Graphics Models
When synthesizing faces using computer graphics (for user interfaces [25], web applications [45], computer games, or special effects in movies), the most common model is a wireframe model or a polygonal mesh. The face is then described as a set of vertices connected with lines forming polygons (usually triangles). The polygons are shaded or texture-mapped, and illumination is added. The texture could be parameterized or fixed—in the latter case facial appearance is changed by moving the vertices only. To achieve life-like animation of the face, a large number (thousands) of vertices and polygons are commonly used. Each vertex can move in three dimensions, so the model requires a large number of degrees of freedom. To reduce this number, some kind of parameterization is needed.
A commonly adopted solution is to create a set of morph targets and blend between them. A morph target is a predefined set of vertex positions, where each morph target represents, for example, a facial expression or a viseme. Thus, the model shape is defined by the morph targets A and controlled by the parameter vector a
The 3N-dimensional vector g contains the 3D coordinates of the N vertices; the columns of the 3N x M-matrix A contain the M morph targets; and a contains the M morph target coefficients. To limit the required computational complexity, most ai values are usually zero.
Morph targets are usually manually created by artists. This is a time consuming process so automatic methods have been devised to copy a set of morph targets from one face model to another [20, 43, 46].
To render the model on the screen, we need to find a correspondence from the model coordinates to image pixels. The projection model (see Sect. 18.2.6), which is not defined by the face model, defines a function P(·) that projects the vertices on the image plane
The image coordinate system is typically defined over the range [-1,1]x[-1,1] or [0,w — 1]x[0,h — 1], where (w, h) is the image dimensions in pixels.
To texturize the model, each vertex is associated with a (prestored) texture coordinate (i, t) defined on the unit square. Using some interpolating scheme (e.g., piecewise affine transformations), we can find a correspondence from any point (x,y,z) on the model surface to a point (i, t) in the texture image and a point (u, v) in the rendered image. Texture mapping is executed by copying (interpolated) pixel values from the texture
to the rendered image of the model
We call the coordinate transform
and thus
While morphing is probably the most commonly used facial animation technique, it is not the only one. Skinning, or bone-based animation, is the process of applying one or more transformation matrices, called bones, to the vertices of a polygon mesh in order to obtain a smooth deformation, for example, when animating joints such as elbow or shoulder. Each bone has a weight that determines its influence on the vertex, and the final position of the vertex is the weighted sum of the results of all applied transformations. While the main purpose of skinning is typically body animation, it has been applied very successfully to facial animation. Unlike body animation, where the configuration of bones resembles the anatomical human skeleton, for facial animation the bones rig is completely artificial and bears almost no resemblance to human skull. Good starting references for skinning are [29, 39]. There are numerous other approaches to facial animation, ranging from ones based on direct modeling of observed motion [48], to pseudo muscle models [35] and various degrees of physical simulation of bone, muscle and tissue dynamics [27, 59, 61].
More on computerized facial animation can be found in [47, 49]. Texture mapping is treated in [23].
Candide: A Simple Wireframe Face Model
Candide is a simple face model that has been a popular research tool for many years. It was originally created by Rydfalk [52] and later extended by Welsh [62] to cover the entire head (Candide-2) and by Ahlberg [2, 3] to correspond better to MPEG-4 facial animation (Candide-3). The simplicity of the model makes it a good pedagogic example.
Candide is a wireframe model with 113 vertices connected by lines forming 184 triangular surfaces. The geometry (shape, structure) is determined by the 3D coordinates of the vertices in a model-centered coordinate system (x,y,z). To modify the geometry, Candide-1 and Candide-2 implement a set of Action Units from FACS. Each AU is implemented as a list of vertex displacements, an Action Unit Vector (AUV), describing the change in face geometry when the Action Unit is fully activated. The geometry is thus parameterized as
where the resulting vector g contains the (x,y,z) coordinates of the vertices of the model, g is the standard shape of the model, and the columns of Φa are the AUVs. The ai values are the Action Unit activation levels.
Candide-3 is parameterized slightly different than the previous versions, generalizing the AUVs to animation modes (implementing AUs or FAPs) and adding shape modes. The parameterization is
The difference between a and σ is that the shape parameters control the static deformations that cause individuals to differ from each other. The animation parameters control the dynamic deformations due to facial action.
This kind of linear model is, in different variations, a common way to model facial geometry. For example, PCA found a matrix that described 2D shape and animation modes combined, Gokturk et al. [22] estimated 3D animation modes using a stereo-vision system, and Caunce et al. [9] created a shape model from models adapted to profile and frontal photos.
To change the pose, the model coordinates are rotated, scaled and translated so that
where π contains the six pose/global motion parameters plus a scaling factor.
Projection Models
The function (u, v) = P(x, y, z), above, is a general projection model representing the camera. There are various projection models from which to chose, each with a set of parameters that may be known (calibrated camera) or unknown (uncalibrated camera). In most applications, the camera is assumed to be at least partly calibrated. We stress that only simple cases are treated here, neglecting such camera parameters as skewness and rotation.
• The simplest projection model is the orthographic projection—basically just throwing away the z-coordinate. Parameters are pixel size
and principal point
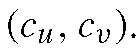The projection can be written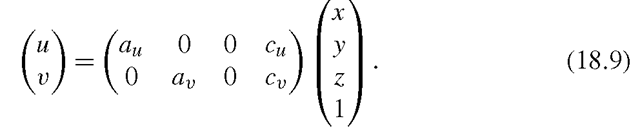
• The most common camera model is the perspective projection, which can be expressed as
where
is the focus of expansion (FOE), and f is the focal length of the camera;
determines the pixel size. Commonly, a simple expression for P
is obtained where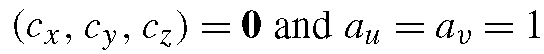
are used. In this case, (18.10) is simply
• The weak perspective projection is an approximation of the perspective projection suitable for an object where the internal depth variation is small compared to the distance zref from the camera to the object.
Tracking Strategies
A face tracking system estimates the rigid or non-rigid motion of a face through a sequence of image frames. In the following, we discuss the two-frame situation, where we have an estimation of the model parameters pik—\ in the old frame, and the system should estimate the parameters pik in the new frame (i.e., how to transform the model from the old frame to the new frame).
As mentioned in the introduction, we discuss only monocular tracking here, that is, we disregard stereo vision systems.
Motion-Based vs. Model-Based Tracking
Tracking systems can be said to be either motion-based or model-based, also referred to as feed-forward or feed-back motion estimation. A motion-based tracker estimates the displacements of pixels (or blocks of pixels) from one frame to another. The displacements might be estimated using optical flow methods (giving a dense optical flow field), block-based motion estimation methods (giving a sparse field but using less computational power), or motion estimation in a few image patches only (giving a few motion vectors only but at very low computational cost).
The estimated motion field is used to compute the motion of the object model using, for example, least-squares, Kalman filtering, or some optimization method. The motion estimation in such a method is consequently dependent on the pixels in two frames; the object model is used only for transforming the 2D motion vectors to 3D object model motion. The problem with such methods is the drifting or the long sequence motion problem. A tracker of this kind accumulates motion errors and eventually loses track of the face. Examples of such trackers can be found in the literature [7, 8, 51].
A model-based tracker, on the other hand, uses a model of the object’s appearance and tries to change the object model’s pose (and possibly shape) parameters to fit the new frame. The motion estimation is thus dependent on the object model and the new frame—the old frame is not regarded except for constraining the search space. Such a tracker does not suffer from drifting; instead, problems arise when the model is not strong or flexible enough to cope with the situation in the new frame. Trackers of this kind can be found in certain articles [5, 31, 33, 56]. Other trackers [11, 13, 22, 36] are motion-based but add various model-based constraints to improve performance and combat drift.
Model-Based Tracking: First Frame Models vs. Pre-trained Models
In general, the word model refers to any prior knowledge about the 3D structure, the 3D motion/dynamics, and the 2D facial appearance. One of the main issues when designing a model-based tracker is the appearance model. An obvious approach is to capture a reference image of the object from the first frame of the sequence. The image could then be geometrically transformed according to the estimated motion parameters, so one can compensate for changes in scale and rotation (and possibly nonrigid motion). Because the image is captured, the appearance model is deterministic, object-specific, and (potentially) accurate. Thus, trackers of this kind can be precise, and systems working in real time have been demonstrated [22, 32, 56, 63].
A drawback with such a first frame model is the lack of flexibility—it is difficult to generalize from one sample only. This can cause problems with changing appearance due to variations in illumination, facial expression, and other factors. Another drawback is that the initialization is critical; if the captured image was for some reason not representative for the sequence (due to partial occlusion, facial expression, or illumination) or simply not the correct image (i.e., if the object model was not correctly aligned in the first frame) the tracker does not work well. Such problems can usually be solved by manual interaction but may be hard to automate.
Note that the model could be renewed continuously (sometimes called an online model), so the model always is based on the previous frame. In this way the problems with flexibility are reduced, but the tracker is then motion-based and might drift.
Another property is that the tracker does not need to know what it is tracking. This could be an advantage—the tracker can track different kinds of objects—or a disadvantage. A relevant example is when the goal is to extract some higher level information from a human face, such as facial expression or lip motion. In that case we need a tracker that identifies and tracks specific facial features (e.g., lip contours or feature points).
A different approach is a pre-trained model-based tracker. Here, the appearance model relies on previously captured images combined with knowledge of which parts or positions of the images correspond to the various facial features. When the model is transformed to fit the new frame, we thus obtain information about the estimated positions of those specific facial features.
The appearance model may be person specific or general. A specific model could, for example, be trained on a database containing images of one person only, resulting in an accurate model for this person. It could cope, to some degree, with the illumination and expression changes present in the database. A more general appearance model could be trained on a database containing many faces in different illuminations and with different facial expressions. Such a model would have a better chance to enable successful tracking of a previously unseen face in a new environment, whereas a specific appearance model presumably would result in better performance on the person and environment for which it was trained. Trackers using pre-trained models of appearance can be found in the literature [5, 31].
Appearance-Based vs. Feature-Based Tracking
An appearance-based or featureless or generative model-based tracker matches a model of the entire facial appearance with the input image, trying to exploit all available information in the model as well as the image. Generally, we can express this as follows:
Assume a parametric generative face model and an input image I of a face from which we want to estimate a set of parameters. The parameters to be extracted should form a subset of parameter set controlling the model. Given a vector p with N parameters, the face model can generate an image Im(p). The principle of analysis-by-synthesis then states that the best estimates of the facial parameters are the ones minimizing the distance between the generated image and the input image
for some distance measure 5(-).
The problem of finding the optimal parameters is a high-dimensional (N dimensions) search problem and thus of high computational complexity. By using clever search heuristics, we can reduce the search time. The trackers described in [5, 31, 33, 36] are appearance-based.
A feature-based tracker, on the other hand, chooses a few facial features that are, supposedly, easily and robustly tracked. Features such as color, specific points or patches, and edges can be used. Typically, a tracker based on feature points tries to estimate the 2D position of a set of points and from these points to compute the 3D pose of the face. Feature-based trackers can be found in [11, 12, 26, 56, 63].
In the following sections, we describe three trackers found in the literature. They represent the classes mentioned above.
Feature-Based Tracking Example
The tracker described in this section tracks a set of feature points in an image sequence and uses the 2D measurements to calculate the 3D structure and motion of the face and the facial features. The tracker is based on the structure from motion (SfM) algorithm by Azerbayejani and Pentland [6]. The (rigid) face tracker was then developed by Jebara and Pentland [26] and further by Strom et al. [56, 57]. The tracker was later extended as to handle non-rigid motion, and thus track facial action by Ingemars and Ahlberg [24].
With the terminology above, it is the first frame model-based and feature-based tracker. We stress that the presentation here is somewhat simplified.
Face Model Parameterization
The head tracker designed by Jebara and Pentland [26] estimated a model as a set of points with no surface. Strom et al. [57] extended the system to include a 3D wireframe face model (Candide). A set of feature points are placed on the surface of the model, not necessarily coinciding with the model vertices. The 3D face model enables the system to predict the surface angle relative to the camera as well as self-occlusion. Thus, the tracker can predict when some measurements should not be trusted.
Pose Parameterization
The pose in the kth frame is parameterized with three rotation angles (rx,ry,rz), three translation parameters (tx,ty,tz), and the inverse focal length φ = 1/f of the camera.1
Azerbayejani and Pentland [6] chose to use a perspective projection model where the origin of the 3D coordinate system is placed in the center of the image plane instead of at the focal point, that is, the FOE is set to (0, 0,1) (see Sect. 18.2.6). This projection model has several advantages; for example, there is only one unknown parameter per feature point (as becomes apparent below).
Thus, the 2D (projected) screen coordinates are computed as
Structure Parameterization
The structure of the face is represented by the image coordinates (u0,v0) and the depth values z0 of the feature points in the first frame. If the depths z0 are known, the 3D coordinates of the feature points can be computed for the first frame as
and for all following frames as
where R is the rotation matrix created. For clarity of presentation, the frame indices on all the parameters are omitted.
All put together, the model parameter vector is
where N is the number of feature points and rx,ry,rz are used to update R. Combining (18.16), (18.17), and (18.15), we get a function from the parameter vector to screen coordinates
Note that the parameter vector has N + 7 degrees of freedom, and that we get 2N values if we measure the image coordinates for each feature point. Thus, the problem of estimating the parameter vector from image coordinates is overconstrained when N > 7.
