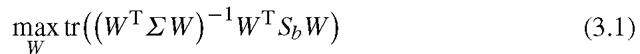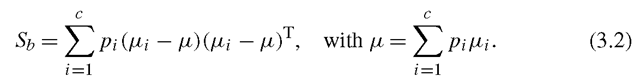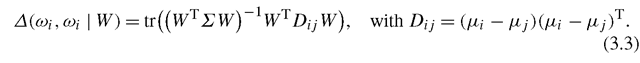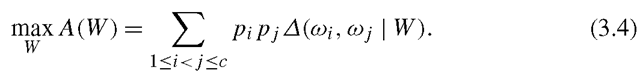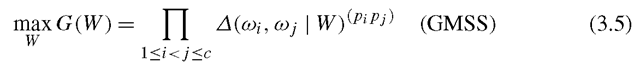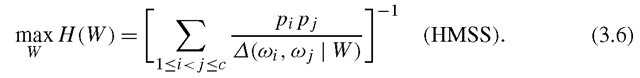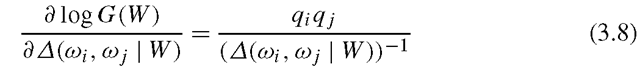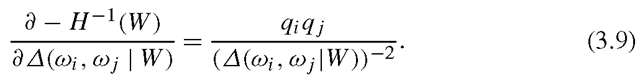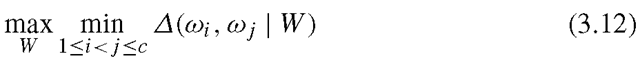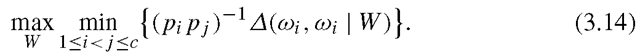Introduction
The last few decades have witnessed a great success of subspace learning for face recognition. From principal component analysis (PCA) [43] and Fisher’s linear discriminant analysis [1], a dozen of dimension reduction algorithms have been developed to select effective subspaces for the representation and discrimination of face images [17, 21, 45, 46, 51]. It has demonstrated that human faces, although usually represented by thousands of pixels encoded in high-dimensional arrays, they are intrinsically embedded in a vary low dimensional subspace [37]. The using of subspace for face representation helps to reduce “the curse of dimensionality” in subsequent classification, and suppress variations of lighting conditions and facial expressions. In this topic, we first briefly review conventional dimension reduction algorithms and then present the trend of recent dimension reduction algorithms for face recognition.
The earliest subspace method for face recognition is Eigenface [43], which uses PCA [23] to select the most representative subspace for representing a set of face images. It extracts the principal eigenspace associated with a set of training face images. Mathematically, PCA maximizes the variance in the projected subspace for a given dimensionality, decorrelates the training face images in the projected subspace, and maximizes the mutual information between appearance (training face images) and identity (the corresponding labels) by assuming that face images are Gaussian distributed. Thus, it has been successfully applied for face recognition. By projecting face images onto the subspace spanned by Eigenface, classifiers can be used in the subspace for recognition. One main limitation of Eigenface is that the class labels of face images cannot be explored in the process of learning the projection matrix for dimension reduction. Another representative subspace method for face recognition is Fisherface [1]. In contrast to Eigenface, Fisherface finds class specific linear subspace. The dimension reduction algorithm used in Fisherface is Fisher’s linear discriminant analysis (FLDA), which simultaneously maximizes the between-class scatter and minimizes the within-class scatter of the face data. FLDA finds in the feature space a low dimensional subspace where the different classes of samples remain well separated after projection to this subspace. If classes are sampled from Gaussian distributions, all with identical covariance matrices, then FLDA maximizes the mean value of the KL divergences between different classes. In general, Fisherface outperforms Eigenface due to the utilized discriminative information.
Although FLDA shows promising performance on face recognition, it has the following major limitations. FLDA discards the discriminative information preserved in covariance matrices of different classes. FLDA models each class by a single Gaussian distribution, so it cannot find a proper projection for subsequent classification when samples are sampled from complex distributions, for example, mixtures of Gaussians. In face recognition, face images are generally captured with different expressions or poses, under different lighting conditions and at different resolution, so it is more proper to assume face images from one person are mixtures of Gaus-sians. FLDA tends to merge classes which are close together in the original feature space. Furthermore, when the size of the training set is smaller than the dimension of the feature space, FLDA has the undersampled problem.
To solve the aforementioned problems in FLDA, a dozen of variants have been developed in recent years. Especially, the well-known undersample problem of FLDA has received intensive attention. Representative algorithms include the optimization criterion for generalized discriminant analysis [44], the unified subspace selection framework [44] and the two stage approach via QR decomposition [52]. Another important issue is that FLDA meets the class separation problem [39]. That is because FLDA puts equal weights on all class pairs, although intuitively close class pairs should contribute more to the recognition error [39]. To reduce this problem, Lotlikar and Kothari [30] developed the fractional-step FLDA (FS-FLDA) by introducing a weighting function. Loog et al. [28] developed another weighting method for FLDA, namely the approximate pairwise accuracy criterion (aPAC). The advantage of aPAC is that the projection matrix can be obtained by the eigenvalue decomposition. Both methods use weighting schemes to select a subspace that better separates close class pairs. Recently, the general mean [39] (including geometric mean [39] and harmonic mean [3]) base subspace selection and the max-min distance analysis (MMDA) [5] have been proposed to adaptively choose the weights.
Manifold learning is a new technique for reducing the dimensionality in face recognition and has received considerable attentions in recent years. That is because face images lie in a low-dimensional manifold. A large number of algorithms have been proposed to approximate the intrinsic manifold structure of a set of face images, such as locally linear embedding (LLE) [34], ISOMAP [40], Laplacian eigen-maps (LE) [2], Hessian eigenmaps (HLLE) [11], Generative Topographic Mapping (GTM) [6] and local tangent space alignment (LTSA) [53]. LLE uses linear coefficients, which reconstruct a given measurement by its neighbors, to represent the local geometry, and then seeks a low-dimensional embedding, in which these coefficients are still suitable for reconstruction. ISOMAP preserves global geodesic distances of all pairs of measurements. LE preserves proximity relationships by manipulations on an undirected weighted graph, which indicates neighbor relations of pairwise measurements. LTSA exploits the local tangent information as a representation of the local geometry and this local tangent information is then aligned to provide a global coordinate. Hessian Eigenmaps (HLLE) obtains the final low-dimensional representations by applying eigen-analysis to a matrix which is built by estimating the Hessian over neighborhood. All these algorithms have the out of sample problem and thus a dozen of linearizations have been proposed, for example, locality preserving projections (LPP) [20] and discriminative locality alignment (DLA) [55]. Recently, we provide a systematic framework, that is, patch alignment [55], for understanding the common properties and intrinsic difference in different algorithms including their linearizations. In particular, this framework reveals that: i) algorithms are intrinsically different in the patch optimization stage; and ii) all algorithms share an almost-identical whole alignment stage. Another unified view of popular manifold learning algorithms is the graph embedding framework [48]. It is shown that manifold learning algorithms are more effective than conventional dimension reduction algorithms, for example, PCA and FLDA, in exploiting local geometry information.
In contrast to conventional dimension reduction algorithms that obtain a low dimensional subspace with each basis being a linear combination of all the original high dimensional features, sparse dimension reduction algorithms [9, 24, 59] select bases composed by only a small number of features of the high dimensional space. The sparse subspace is more interpretable both psychologically and physiologically. One popular sparse dimension reduction algorithm is sparse PCA, which generalizes the standard PCA by imposing sparsity constraint on the basis of the low dimensional subspace. The Manifold elastic net (MEN) [56] proposed recently is another sparse dimension reduction algorithm. It obtains a sparse projection matrix by imposing the elastic net penalty (i.e., the combination of the lasso penalty and the L2-norm penalty) over the loss (i.e., the criterion) of a discriminative manifold learning, and formulates the problem as lasso which can be efficiently solved. In sum, sparse learning has many advantages, because (1) sparsity can make the data more succinct and simpler, so the calculation of the low dimensional representation and the subsequent recognition becomes more efficient. Parsimony is especially important for large scale face recognition systems; (2) sparsity can control the weights of original variables and decrease the variance brought by possible over-fitting with the least increment of the bias. Therefore, the learn model can generalize better and obtain high recognition rate for distorted face images; and (3) sparsity provides a good interpretation of a model, thus reveals an explicit relationship between the objective of the model and the given variables. This is important for understanding face recognition.
One fundamental assumption in face recognition, including dimension reduction, is that the training and test samples are independent and identically distributed (i.i.d.) [22, 31, 38]. It is, however, very possible that this assumption does not hold, for example, the training and test face images are captured under different expressions, postures or lighting conditions, letting alone test subjects do not even appear in the training set [38]. Transfer learning has emerged as a new learning scheme to deal with such problem. By properly utilizing the knowledge obtained from the auxiliary domain task (training samples), it is possible to boost the performance on the target domain task (test samples). The idea of cross domain knowledge transfer was also introduced to subspace learning [31, 38]. It has shown that by using transfer subspace learning, the recognition performance on the cases where the face images in training and test sets are not identically distributed can be significantly improved compared with comparison against conventional subspace learning algorithms.
The rest of this topic presents three groups of dimension reduction algorithms for face recognition. Specifically, Sect. 3.2 presents the general mean criterion and the max-min distance analysis (MMDA). Section 3.3 is dedicated to manifold learning algorithms, including the discriminative locality alignment (DLA) and manifold elastic net (MEN). The transfer subspace learning framework is presented in Sect. 3.4. In all of these sections, we first present principles of algorithms and then show thorough empirical studies.
Subspace Learning—A Global Perspective
Fisher’s linear discriminant analysis (FLDA) is one of the most well-known methods for linear subspace selection, and has shown great value in subspace based face recognition. Being developed by Fisher [14] for binary-class classification and then generalized by Rao [33] for multiple-class tasks, FLDA utilizes the ratio of the between-class to within-class scatter as a definition of discrimination. It can be verified that under the homoscedastic Gaussian assumption, FLDA is Bayes optimal [18] in selecting a c — 1 dimensional subspace, wherein c is the class number. Suppose there are c classes, represented by homoscedastic Gaussians
with the prior probability
is the mean of class ωι and Σ is the common covariance. The Fisher’s criterion is given by [15]
where
It has been pointed out that the Fisher’s criterion implies the maximization of the arithmetic mean of the pairwise distances between classes in the subspace. To see this, let us first define the distance between classes ωι and ω j in the subspace W as
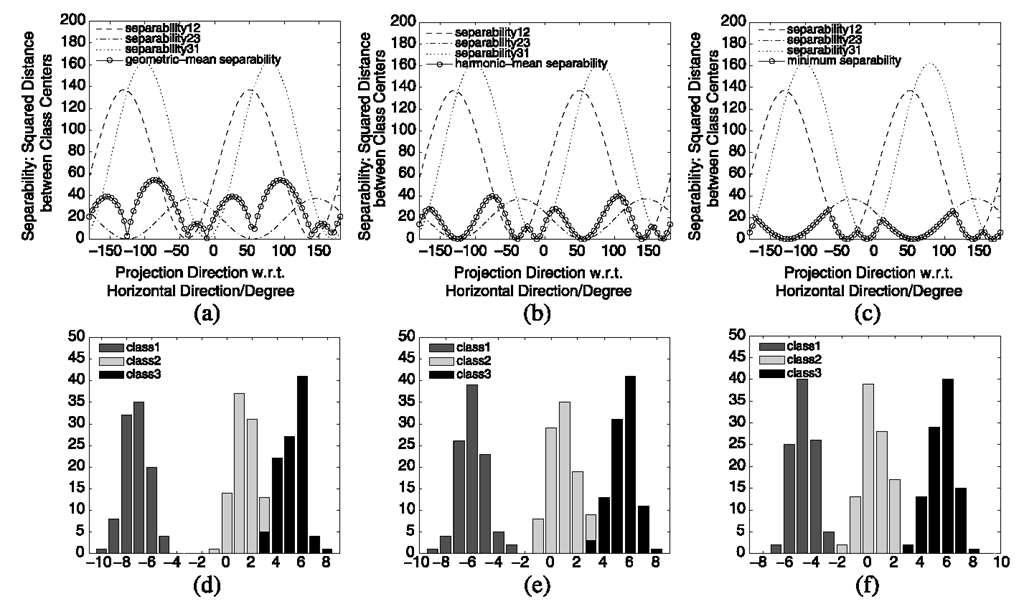
Fig. 3.1 An illustrative example on the class separation problem of FLDA. a 2-dimensional scatter plot of three classes, b plots of pairwise separabilities and the arithmetic mean (FLDA) separability verse projection directions, from -180 degree to 180 degree with respect to horizontal direction in (a), and c shows the histogram of three classes projected onto the FLDA direction, which is around 66 degree
Then, simple algebra shows that (3.1) is equivalent to the arithmetic mean criterion below
We call it arithmetic mean based subspace selection (AMSS). Since the arithmetic mean of all pairwise distance is used as the criterion, one apparent disadvantage of (3.4) is that it ignores the major contributions of close class pairs to classification error and may cause the merge of those class pairs in the selected subspace. Such phenomenon of FLDA or AMSS is called the class separation problem [39].
Figure 3.1 illustrates the class separation problem of FLDA [5]. In the toy example, three class are represented by homoscedastic Gaussian distributions on the two dimensional space. And we want to find a one dimensional subspace (or projection direction) such that the three classes can be well separated. Varying the one dimensional subspace, that is, changing the angle of projection direction with respect to the horizontal direction, the three pairwise distances change. FLDA finds the subspace that maximizes the average of the three pairwise distances. However, as illustrated, the obtained one dimensional subspace by FLDA severely merges the blue and green classes.
General Mean Criteria
To improve the separation between close class pairs, the general mean criteria has been proposed by Tao et al., of which two examples are the geometric mean based subspace selection (GMSS) [39] and the harmonic mean based subspace selection (HMSS) [3]
and
We give an mathematical analysis to interpret how criteria (3.5) and (3.6) work in dealing with the class separation problem, and why criterion (3.6) is even better than criterion (3.5). Consider a general criterion below
In order to reduce the class separation problem, the objective J(W) must has the ability to balance all the pairwise distances. We claim that this ability relies on the partial derivative of J(W) with respect to the pairwise distances. Apparently, an increment of any
will enlarge J(W), and for this an small one should have bigger inference, because from the classification point of view when the distance between two classes is small then any increment of the distance will significantly improve the classification accuracy, but when the distance is large enough then the improvement of accuracy will be ignorable (it is well known that for Gaussian distribution the probability out the range of ±3σ is less than 0.01%). Besides, the partial derivatives must vary as the varying of the pairwise distances so as to take account of the current values of the pairwise distances in the procedure of subspace selection, but not only the initial distances in the original high dimensional space. According to the discussion above, the partial derivatives must be monotone decreasing functions of
. In the cases of criteria (3.4) and (3.5), we set
, and then the derivatives are calculated as below
and
We can see that in both cases the partial derivative monotonically decreases with respect to the pairwise distance and thus provides the ability to reduce the class separation problem. However, note that the order of decreasing for HMSS is higher than that for GMSS (—2 vs —1), which implies that HMSS is more powerful than GMSS in reducing the class separation problem. Besides, as
increases, we have
Fig. 3.2 GMSS, HMSS and MMDA for the same three-class problem in Fig. 3.1: first column, GMSS; second column, HMSS; third column, MMDA. Top row shows plots of pairwise separations and the separations by different criteria, i.e., GMSS, HMSS and MMDA. Bottom row shows the histograms of the three classes projected onto the GMSS, HMSS and MMDA directions, which are around 93 degree, 104 degree and 115 degree, respectively
but
The logarithm value (3.10) is unbounded, and thus in GMSS a large pairwise distance still possibly affects small ones. In contrast, the bounded result (3.11) makes HMSS is more favorable. To solve the maximization problems of (3.5) and (3.6), [39] provides a gradient descent algorithm with a projection onto the orthogonal constraint set. Further, [3] suggests exploiting the structure of orthogonal constraint and optimizing the subspace on the Grassmann manifold [12]. For details of these optimization algorithms, please refer to [39] and [3]. The corresponding results of GMMS and HMSS on the illustrative example in Fig. 3.1 are shown in Fig. 3.2. One can see that the merged class pair in the FLDA subspace is better separated by using the more sophisticated methods.
Max-Min Distance Analysis
Previous discussions show that GMSS and HMSS are able to reduce the class separation problem of FLDA. Such merits come from the inherence of geometric or harmonic means in adaptively emphasizing small pairwise distance between classes. A further question is: can we select a subspace that mostly considers small pairwise distance? Namely, we may intend to find an optimal subspace which gives the maximized minimum pairwise distance. Generally, such aim cannot be achieved by GMSS or HMSS, neither other subspace selection methods. To this end, [5] proposed the max-min distance analysis (MMDA) criterion,
where the inner minimization chooses the minimum pairwise distance of all class pairs in the selected subspace, and the outer maximization maximizes this minimum distance. Let the optimal value and solution of (3.12) be .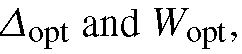
and then we have
which ensures the separation (as best as possible) of any class pairs in the selected low dimensional subspace. Furthermore, by taking the prior probability of each class into account, the MMDA criterion is given by
Note that, the use of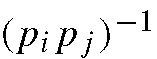
as weighting factor is an intuitive choice. In order to obtain a relatively high accuracy, it has to put more weight on classes with high prior probabilities; however, because the minimization in the max-min operation has a negative effect, we need to put a smaller factor, for example, the inverse factor 
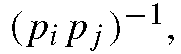on the pairwise distance between high-prior probability classes so that it has a greater chance to be maximized.
The solving of MMDA criteria (3.12) and (3.14) can be difficult. The inner minimizations there are over discrete variables i and j, and thus it makes the objective function for the outer maximization nonsmooth. To deal with this nonsmooth max-min problem [5] introduced the convex relaxation technique. Specifically, the authors proposed a sequential semidefinite programming (SDP) relaxation algorithm, with which an approximate solution of (3.12) or (3.14) can be obtained in polynomial time. Refer to [5] for details of the algorithm. The MMDA result on the illustrative example in Fig. 3.1 is shown in Fig. 3.2, from which one can see that MMDA gives the best separation between blue and green classes among the four criteria.
Empirical Evaluation
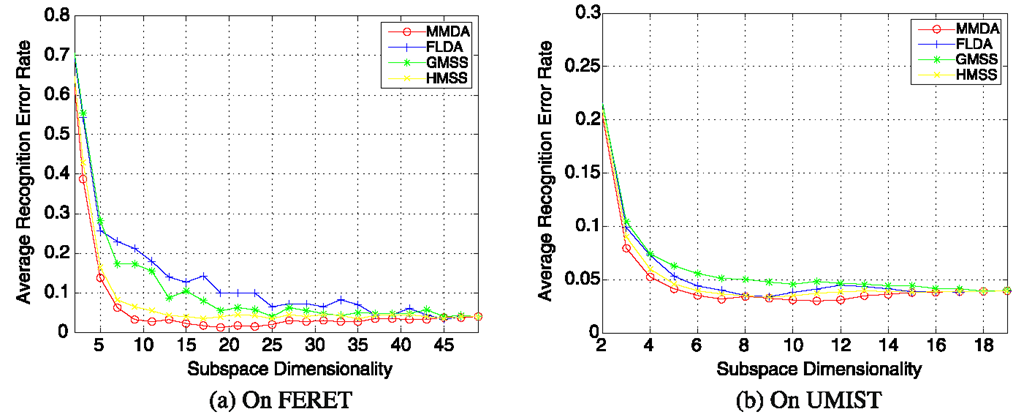
The evaluation of general mean criteria, including GMSS and HMSS, and the MMDA are conducted on two benchmark face image datasets, UMIST [1] and FERET [32]. The UMIST database consists of 564 face images from 20 individuals. The individuals are a mix of race, sex and appearance and are photographed in a range of poses from profile to frontal views. The FERET database contains 13 539 face images from 1565 subjects, with varying pose, facial expression and age. 50 subjects with 7 images for each are used in the evaluation.
Fig. 3.3 Face recognition by subspace selection and nearest neighbor classification in the selected low dimensional subspace
Images from both databases are cropped with reference to the eyes, and normalized to 40 by 40 pixel arrays with 256 gray levels per pixel. On UMIST, 7 images for each subject are used for training and the rest images are used for test, while on FERET, a 6 to 1 split is used for training/test setup. The average recognition performances over ten random trials are shown in Fig. 3.3. One can see that, on FERET, the general mean criterion (GMSS and HMSS) and MMDA show significant improvements on recognition rate compared with FLDA, while on UMIST, though GMSS gives slight inferior performance to FLDA, HMSS and MMDA still improve the performance in certain extent.
