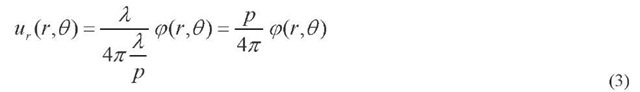ABSTRACT
This paper describes three different optical systems designed to be used outside the lab for pipeline inspections. The first one is a robust and portable ESPI based hole-drilling unit with radial sensitivity used for residual stresses measurement. The device has a special diffractive optical element that produces an achromatic interferometer. The displacement component around the hole drilled is measured by ESPI with radial in-plane sensitivity and is fitted by least square methods to evaluate residual stresses. An infield application for analyzing the integrity of a gas pipeline is presented as an application example. The second system is a conical laser triangulation device to measure the geometry of the inner surface of pipes. A laser beam is deflected by the tip of a 45° conical mirror and produces a radial light plane that intercepts the inner surface of the pipe producing a bright ring all way around 360°. The image of the light ring is used to compute the radius of about 1400 points in each section while the device is moved along the pipe axis. Finally, the third system uses active photogrammetry to measure in cylindrical coordinates the details of the inner geometry of pipe junctions and welding seams. It was designed to inspect welded joints, to check weld seam quality as well as to identify transverse and angular misalignment between adjacent sections.
Introduction
Light is a very rich and powerful information carrier. Intensity, trajectory, wavelength/color, polarization state, speed and coherence state are light properties that can carry information. The ability to manipulate light to change one or more property as a function of a quantity of interest is the basic principle behind any optical measurement principle. Mechanical, chemical, electrical, thermal, temporal quantities can be measured by optical methods. It is possible to measure quantities in the nano world as well to measure distances of remote galaxies over 1025 m far away from earth.
From the engineering point of view, optical measurement methods are very attractive for two main reasons: high speed and non-invasiveness. The ability to measure at the light speed makes it possible to handle highly dynamic events and to acquire a large amount of data in a very short time. Light usually does not scratch, deform, wear or damage most engineering surfaces or materials. However, light behavior can be influenced by environmental disturbances like temperature, moisture, vibration, dust or pressure, what make the design of an optical measurement system a careful task. That task is even more challenging if the system has to operate in harsh environments.[1]
This paper presents three optical measurement systems designed to operate out of the laboratory environment. The first one is an optical digital speckle patter interferometer (DSPI or ESPI) with a special configuration to reach radial in-plane sensitivity.[2-6] It is integrated with a high speed drilling unit to measure residual stresses using the incremental hole drilling technique. This paper reports an application of this system that uses the residual stresses values to access the external loading applied to a gas pipeline exposed to surrounding soil movement. The second optical system is an optical profilometer that uses a special laser triangulation configuration with a conical mirror to measure the internal geometry of pipes.[9] It was designed to inspect the inner surface of pipes for corrosion. Finally, the third system is another optical profilometer that uses a special optical configuration to measure in high resolution the inner geometry of pipes using active photogrammetry.[10, 11] It was designed to inspect welded pipe joints for misalignments and to verify weld seams quality.
Cartesian coordinate systems are frequently used for most engineering applications. They are appropriate when the quantity has a rectangular domain. However, there is a class of engineering problems where polar or cylindrical coordinate systems are the natural choice. The radial digital speckle pattern interferometer measures the displacement field around the hole drilled in polar coordinates. The two profilometers do the measurement and process the results in cylindrical coordinates. Those characteristics make the systems very appropriate for the target applications.
Radial in-plane ESPI interferometer
There are two basic ways to illuminate the measured surface in digital speckle pattern interferometry (DSPI or ESPI): single illumination or double illumination.[8] In the first case, only one light source is directed to the surface. The interference is produced with the aid of another reference illumination, which can be directed to the camera sensor or to an auxiliary surface. Single illumination is mostly used to perform out-of-plane displacement measurements. In double illumination, coherent light coming from two different directions illuminates the surface. The interference is produced by the mutual interaction between the two light components. This configuration is preferable for in-plane displacement measurements. The sensitivity direction in a given point P is defined by the vector difference between two unitary vectors pointing from P to each illumination source. If the illumination directions are symmetrical to the surface normal, the resulting sensitivity vector is parallel to the measured surface, what is the ideal configuration of measuring in-plane displacements. In order to measure the complete in-plane 2D displacement field, two double illumination configurations are needed and their data combined.
The interferometer
The author’s group developed a double illumination digital speckle pattern interferometer with in -plane sensitivity in polar coordinates.[2-7] In order to obtain in-plane sensitivity in the radial direction a special diffractive optical element was developed. This configuration is very suitable for engineering applications since it is possible to measure the stress state from a unique illumination scheme.
Figure 1 shows a sketch of the special diffractive optical element (DOE). It is a binary phase diffraction grid with about 1000 concentric circles per millimeter. Its shape is like the disk shown in the left part of the figure with about 30 mm diameter. The diffractive area is represented in gray. A central clear window is left for viewing proposes. The middle of the figure shows a cross section along a diametric line of the DOE displaying four particularly chosen light rays from a collimated illumination source, which are diffracted by the DOE. Only the first diffraction order is shown in the figure, what bends the light rays toward the center of the circular region. If a point P is particularly considered, diffracted rays illuminate it symmetrically along the illumination directions indicated by the unitary vectors kt and k2. Sensitivity direction is given by the vector k obtained from the subtraction of the two unitary ones. Since the angles are symmetrical for both light rays, in-plane sensitivity is reached at point P in the radial direction. The same conclusion is valid for any other point on a diametral line, producing radial in-plane sensitivity in the central circular area. The only exception is the center of the circular region that receives light from all directions and is a singular point.
Figure 1: Cross section of the diffractive optical element showing the principle of radial in-plane sensitivity.
A chromaticity
It can be verified that the configuration described in Figure 1 is achromatic, i.e., the measurement sensitivity does not depends on the laser wavelength. A monochromatic light ray that goes through an ordinary diffraction grating is split in several diffraction orders. The angle ft between the incident ray and the first diffraction order is given by equation (1):
where
is the light wavelength and p is the diffraction grating period. A small variation in the wavelength will change the diffraction angle ft. The relationship between the radial in-plane displacement component
and the optical phase distribution
for the radial in-plane interferometer presented in Figure 1 is given by: 
where r and 6 are the polar coordinates and ft the first order diffraction angle. Since the diffraction angle is given by equation (1), the value of sin ft can be replaced in equation (2):
According to equation (3), the relationship between the displacement field and the optical phase distribution only depends on p, the period of the grating, and not on laser wavelength. This configuration allows the use of non-wavelength stabilized diode lasers, which are compact, robust and a lot less expensive. The sensitivity of the interferometer is only a function of the stability of the pitch of the diffractive optical element, which in a silicon substrate typically changes only about 0.0004% for temperature variations of 1 kelvin.
Equipment for residual stresses measurement
Figure 2 shows a practical realization of the achromatic radial in-plane interferometer. Expanded light from a diode laser (L) passes through a central hole of mirror M1 and illuminates mirrors M2 and M3. The laser is reflected back to mirror M1 being directed to the lens (CL) to obtain an annular collimated beam. Finally, the light is diffracted by the first order of the diffractive optical element is symmetrically directed from both sides towards the specimen surface. Mirror M2 is attached to a piezo translator (PZT) to introduce a constant phase shift between both illuminations in order to calculate wrapped phase maps using phase shifting algorithms.
Figure 2: Practical realization of the radial in-plane interferometer.
Figure 3 shows the complete set used for residual stresses measurement. A universal base is rigidly attached to the specimen surface by four rare earth magnets combined with three rods with sharp conical tips. The optical head is shown in the right part. The left part shows the hole drilling unit equipped with a high speed pneumatic turbine. A kinematic mounting scheme makes the positioning and replacement of both modules to the universal base very repeatable. After attaching the universal base to the surface where the residual stresses have to be measured, the optical measurement module (OMM) is positioned in the universal base and an initial phase pattern is acquired and digitally stored. After that, the OMM is removed and replaced by the high speed drilling module (HSDM). The drilling is done until a predefined depth is reached. Air is continuously blown during the drilling to remove metal chips from the measurement area. The HSDM is removed and the OMM positioned again and another phase pattern is acquired. The process is sequentially repeated until the predefined number of drilling increments is reached. After that, the phase differences are calculated, digitally processed and the residual stresses computed. The total measurement time depends on the number of increments. However it is typically only 25% of the time required to do the same measurement with hole drilling and strain gauges.
Figure 3: The set used for in-field residual stresses measurement. Left: hole drilling unit; central: universal base and right: optical measurement module.
