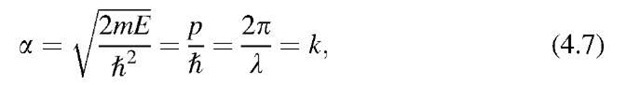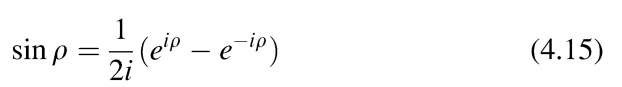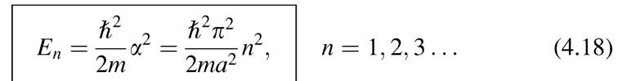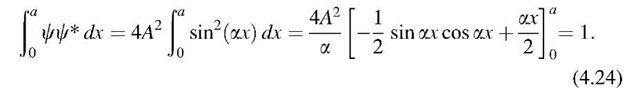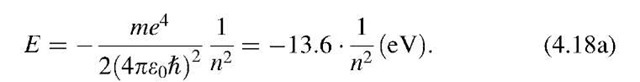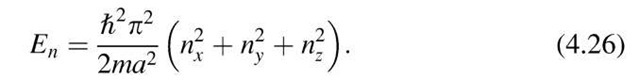Free Electrons
At first we solve the Schrodinger equation for a simple but, nevertheless, very important case. We consider electrons which propagate freely, i.e., in a potential-free space in the positive x-direction. In other words, it is assumed that no "wall," i.e., no potential barrier (V), restricts the propagation of the electron wave. The potential energy V is then zero and the Schrodinger equation (3.1) assumes the following form:
This is a differential equation for an undamped vibration3 with spatial periodicity whose solution is known to be3
where
3
(For our special case we do not write the second term in (A.5) ,
because we stipulated above that the electron wave3 propagates only in the positive x-direction and not, in addition, in the negative x-direction.)
Figure 4.1. Energy continuum of a free electron (compare with Fig. 4.3).
From (4.3), it follows that
Since no boundary condition had to be considered for the calculation of the free-flying electron, all values of the energy are "allowed," i.e., one obtains an energy continuum (Fig. 4.1). This statement seems to be trivial at this point. The difference to the bound electron case will become, however, evident in the next section.
Before we move ahead, letus combine equations (4.3), (2.3), and (1.4), i.e.,
which yields
The term 2p/1 was defined in (2.5) to be the wave number, k. Thus, a is here identical with k. We see from (4.7) that the quantity k is proportional to the momentum p and, because of p = mv, also proportional to the velocity of the electrons. Since both momentum and velocity are vectors, it follows that k is a vector, too. Therefore, we actually should write k as a vector which has the components kx, ky, and kz:
Since k is inversely proportional to the wavelength, l, it is also called the "wave vector." We shall use the wave vector in the following sections frequently. The k-vector describes the wave properties of an electron, just as one describes in classical mechanics the particle property of an electron with the momentum. As mentioned above, k and p are mutually proportional, as one can see from (4.7). The proportionality factor is 1/\.
Electron in a Potential Well (Bound Electron)
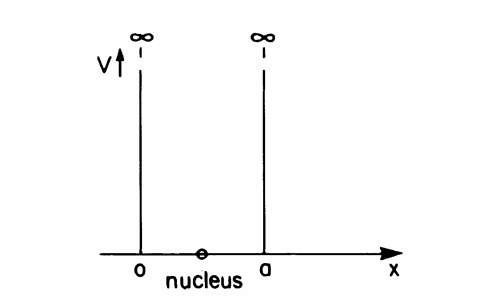
We now consider an electron that is bound to its atomic nucleus. For simplicity, we assume that the electron can move freely between two infinitely high potential barriers (Fig. 4.2). The potential barriers do not allow the electron to escape from this potential well, which means that C = 0 for x C 0 and x S a. We first treat the one-dimensional case just as in Section 4.1, i.e., we assume that the electron propagates only along the x-axis. However, because the electron is reflected on the walls of the well, it can now propagate in the positive, as well as in the negative, x-direction. In this respect, the present problem is different from the preceding one. The potential energy inside the well is zero, as before, so that the Schrodinger equation for an electron in this region can be written, as before,
Because of the two propagation directions of the electron, the solution of (4.10) is
(see topic 1), where
We now determine the constants A and B by means of boundary conditions. We just mentioned that at x C 0 and x S a the C function is zero. This boundary condition is similar to that known for a vibrating string, which does not vibrate at the two points where it is clamped down. (See also Fig. 4.4(a).) Thus, for x = 0 we stipulate C = 0. Then we obtain from (4.11)
Figure 4.2. One-dimensional potential well. The walls consist of infinitely high potential barriers.
Similarly, we stipulate C = 0 for x = a. Using this boundary condition and (4.13), equation (4.11) becomes
With the Euler equation
(see topic 2), we rewrite Equation (4.14)
Equation (4.16) is only valid if sin a a = 0, i.e., if
(because 2, A, and i cannot be zero).
Substituting the value of a from (4.12) into (4.17) provides (We exclude n = 0, which would yield C = 0, that is, no electron wave.)
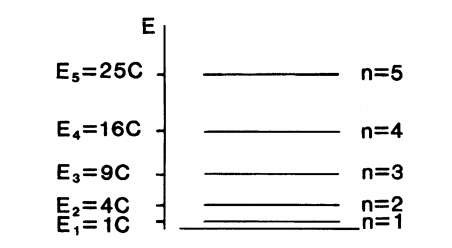
We notice immediately a striking difference from the case in Section 4.1. Because of the boundary conditions, only certain solutions of the Schrodinger equation exist, namely those for which n is an integer. In the present case the energy assumes only those values which are determined by (4.18). All other energies are not allowed. The allowed values are called "energy levels." They are shown in Fig. 4.3 for a one-dimensional case. Because of the fact that an electron of an isolated atom can assume only certain energy levels, it follows that the energies which are excited or absorbed also possess only discrete values. The result is called an "energy quantization." The lowest energy that an electron may assume is called the "zero-point energy". It can be calculated from (4.18) for n = 1. In other words, the lowest energy of the electron is not that of the bottom of the potential well, but rather a slightly higher value.
Figure 4.3. Allowed energy values of an electron that is bound to its atomic nucleus. E is the excitation energy in the present case. C = \2p2/2ma2, see (4.18). (E1 is the zero-point energy).
We discuss now the wave function, C, and the probability CC* for finding an electron within the potential well (see topic 2). According to (4.11), (4.13), and the Euler equation (4.15), we obtain within the well
and the complex conjugate of
The product
is then
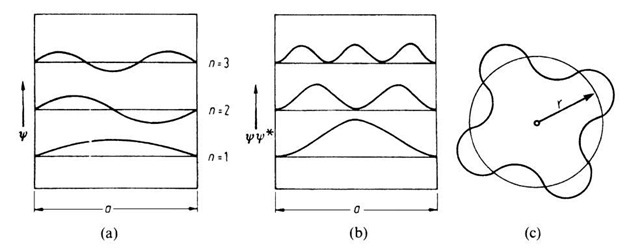
Equations (4.19) and (4.21) are plotted for various n-values in Fig. 4.4. From Fig. 4.4(a), we see that standing electron waves are created between the walls of the potential well. Note that integer multiples of half a wavelength are equal to the length, a, of the potential well. The present case, in its mathematical treatment, as well as in its result, is analogous to that of a vibrating string.
Of special interest is the behavior of the function CC*, i.e., the probability of finding the electron at a certain place within the well (Fig. 4.4(b)). In the classical case the electron would travel back and forth between the walls. Its probability function would therefore be equally distributed along the whole length of the well. In wave mechanics the deviation from the classical case is most pronounced for n = 1. In this case, CC* is largest in the middle of the well and vanishes at the boundaries. For n = 2, the probability of finding an electron at the center of the well (and at the boundaries) is zero, whereas the largest CC* is found at 1 a and 4 a. For successively higher n-values, i.e., for higher energies, the wave mechanical values for CC* are eventually approaching the classical value.
In order to deepen the understanding of the behavior of bound electrons, the reader is reminded of the Rutherford model (topic 2), in which the electrons are described to move in distinct orbits about a positively charged nucleus.
Figure 4.4. (a) C function and (b) probability function CC* for an electron in a potential well for different n-values. (c) Allowed electron orbit of an atom.
Similarly, as shown in Fig. 4.4(a), the electron waves associated with an orbiting electron have to be standing waves. If this were not the case, the wave would be out of phase with itself after one orbit. After a large number of orbits, all possible phases would be obtained and the wave would be annihilated by destructive interference. This can only be avoided if a radius is chosen so that the wave joins on itself (Fig. 4.4(c)). In this case the circumference, 2pr, of the orbit is an integer multiple, n, of the wavelength, l, or
which yields
This means that only certain distinct orbits are allowed, which brings us back to the allowed energy levels which we discussed above. Actually, this model was proposed in 1913 by Niels Bohr.
*For the above discussions, we did not need to evaluate the constant ‘A’. Those readers who are interested in this detail may simply rewrite (4.21) in conjunction with (3.15):
Inserting the boundaries in (4.24) and using (4.17) provides
*The results that are obtained by considering an electron in a square well are similar to the ones which one receives when the wave mechanical properties of a hydrogen atom are calculated. As above, one considers an electron with charge — e to be bound to its nucleus. The potential, V, in which the electron propagates is taken as the Coulombic potential V = —e2/(4pe0r). Since V is a function of the radius, r, the Schrodinger equation is more conveniently expressed in polar coordinates. Of main interest are, again, the conditions under which solutions to this Schrodinger equation exist. The treatment leads, similarly as above, to discrete energy levels:
The main difference compared to the square well model is, however, that the energy is now proportional to —1/n2 (and not to n2 as in (4.18)). This results in a "crowding" of energy levels at higher energies.
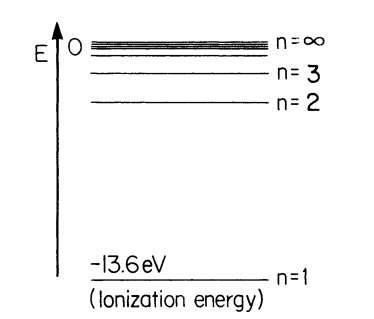
Figure 4.5. Energy levels of atomic hydrogen. E is the binding energy.
The energy at the lowest level is called the ionization energy, which has to be supplied to remove an electron from its nucleus. Energy diagrams, as in Fig. 4.5, are common in spectroscopy. The origin of the energy scale is arbitrarily set at n = 1 and the ionization energies are counted negative. Since we are mainly concerned with the solid state, the detailed calculation of the hydrogen atom is not treated here.
*So far, we have considered the electron to be confined to a one-dimensional well. A similar calculation for a three-dimensional potential well ("electron in a box") leads to an equation which is analogous to (4.18):
The smallest allowed energy in a three-dimensional potential well is occupied by an electron if nx = ny = nz = 1. For the next higher energy there are three different possibilities for combining the n-values; namely, (nx, ny, nz) = (1, 1, 2), (1, 2, 1), or (2, 1, 1). One calls the states which have the same energy but different quantum numbers "degenerate" states. The example just given describes a threefold degenerate energy state.