Introduction
The understanding of the behavior of electrons in solids is one of the keys to understanding materials. The electron theory of solids is capable of explaining the optical, magnetic, thermal, as well as the electrical properties of materials. In other words, the electron theory provides important fundamentals for a technology which is often considered to be the basis for modern civilization. A few examples will illustrate this. Magnetic materials are used in electric generators, motors, loudspeakers, transformers, tape recorders, and tapes. Optical properties of materials are utilized in lasers, optical communication, windows, lenses, optical coatings, solar collectors, and reflectors. Thermal properties play a role in refrigeration and heating devices and in heat shields for spacecraft. Some materials are extremely good electrical conductors, such as silver and copper; others are good insulators, such as porcelain or quartz. Semiconductors are generally poor conductors at room temperature. However, if traces of certain elements are added, the electrical conductivity increases.
Since the invention of the transistor in the late 1940s, the electronics industry has grown to an annual sales level of about five trillion dollars. From the very beginning, materials and materials research have been the lifeblood of the electronics industry.
For the understanding of the electronic properties of materials, three approaches have been developed during the past hundred years or so which differ considerably in their philosophy and their level of sophistication. In the nineteenth century, a phenomenological description of the experimental observation was widely used. The laws which were eventually discovered were empirically derived. This "continuum theory" considered only macroscopic quantities and interrelated experimental data. No assumptions were made about the structure of matter when the equations were formulated. The conclusions that can be drawn from the empirical laws still have validity, at least as long as no oversimplifications are made during their interpretation. Ohm’s law, the Maxwell equations, Newton’s law, and the Hagen-Rubens equation may serve as examples.
A refinement in understanding the properties of materials was accomplished at the turn to the twentieth century by introducing atomistic principles into the description of matter. The "classical electron theory" postulated that free electrons in metals drift as a response to an external force and interact with certain lattice atoms. Paul Drude was the principal proponent of this approach. He developed several fundamental equations that are still widely utilized today. We will make extensive use of the Drude equations in subsequent parts of this topic.
A further refinement was accomplished at the beginning of the twentieth century by quantum theory. This approach was able to explain important experimental observations which could not be readily interpreted by classical means. It was realized that Newtonian mechanics become inaccurate when they are applied to systems with atomic dimensions, i.e., when attempts are made to explain the interactions of electrons with solids. Quantum theory, however, lacks vivid visualization of the phenomena which it describes. Thus, a considerable effort needs to be undertaken to comprehend its basic concepts; but mastering its principles leads to a much deeper understanding of the electronic properties of materials.
The first part of the present topic introduces the reader to the fundamentals of quantum theory. Upon completion of this part the reader should be comfortable with terms such as Fermi energy, density of states, Fermi distribution function, band structure, Brillouin zones, effective mass of electrons, uncertainty principle, and quantization of energy levels. These concepts will be needed in the following parts of the topic.
It is assumed that the reader has taken courses in freshman physics, chemistry, and differential equations. From these courses the reader should be familiar with the necessary mathematics and relevant equations and definitions, such as:
Newton’s law: force equals mass times acceleration (F = ma); (1.1)
Kinetic energy:![]() (v is the particle velocity); (1.2)
(v is the particle velocity); (1.2)
Momentum: p = mv;(1.3)
Combining (1.2) and (1.3) yields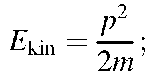 (1.4)
(1.4)
Speed of light:![]() (n = frequency of the light wave, and n 5)
(n = frequency of the light wave, and n 5)
l its wavelength); ( .
Einstein’s mass—energy equivalence:![]() (1.8)
(1.8)
It would be further helpful if the reader has taken an introductory course in materials science or a course in crystallography in order to be familiar with terms such as lattice constant, Miller’s indices, X-ray diffraction, Bragg’s law, etc. Regardless, these concepts are briefly summarized in this text whenever they are needed. In order to keep the topic as self-contained as possible, some fundamentals in mathematics and physics are summarized in the Appendices.
