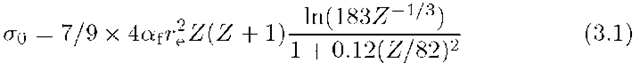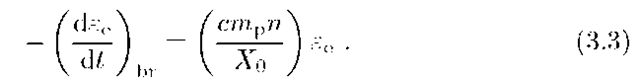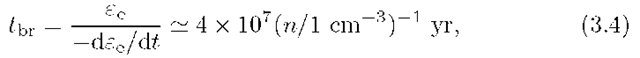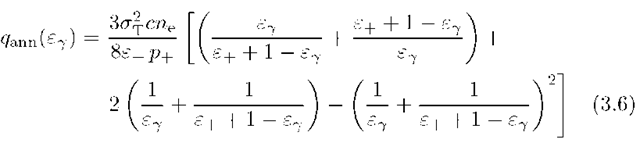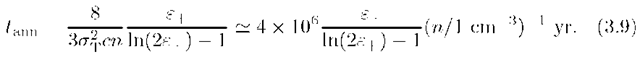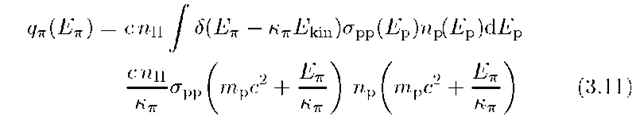Any interpretation of an astronomical observation requires, by definition, unambiguous identification of the relevant radiation mechanism(s). The adequate knowledge of the features of the principal radiation processes is another key issue. Therefore the physics of radiation and absorption mechanisms is one of the central subjects of astronomy. With some exceptions, all basic radiation processes relevant to astronomy have been studied in great detail using the methods and tools of the modern experimental and theoretical physics, in particular the atomic and molecular physics, nuclear physics, high energy (particle) physics. Generally, each wavelength band in astronomy is characterised by one or two basic radiation mechanisms. However, this is not the case of gamma-ray astronomy. Here we deal with a large number of competing processes which makes the theoretical studies very interesting, but also challenging. Very often, we face a dilemma when the same experimental result can be equally well explained by more than one radiation mechanism. For example, for explanation of the TeV Y-radiation from blazars at least four different possible channels associated with the inverse Compton scattering of electrons, as well as with interaction of protons with magnetic field (synchrotron radiation), photon fields (photo-meson processes) and matter (inelastic p-p collisions) have been proposed, and, at this stage, none of them can be firmly discarded. Even in simpler scenarios, like Y-ray production in supernova remnants, a basic question of the dominant radiation mechanism remains unsolved. Moreover, sometimes two or more radiation processes contribute comparably to the same energy interval of the observed Y-ray flux. This is the case, for example, of diffuse radiation of the Galactic Disk at MeV and GeV energies.
The unambiguous identification of Y-ray production mechanisms in celestial objects requires not only comprehensive experimental data containing information about the spectral, temporal and spatial properties of radi-ation1 , but also clear understanding of the features of relevant elementary processes and their relationships to each other, especially in the context of multi wavelength studies.
Apart from the emission by thermal relativistic plasmas, Y-ray production in astronomical environments implies interactions of accelerated particles (electrons, protons and nuclei) with ambient targets – thermal gas, low-frequency photons, magnetic fields. There are several possible ways of grouping different radiative processes by character of interactions (leptonic or hadronic, absorption or radiation) or by type of the target. Below we adopt the latter classification which allows a rather convenient description of relative contributions of different processes for a given astronomical environment dominated by matter, radiation or magnetic field. The cross-sections of all electromagnetic processes are calculated within the framework of Quantum Electrodynamics. These results, obtained with an extremely high accuracy, are summarised in many famous monographs (e.g. Heitler, 1954; Jauch and Rohrlich, 1955; Akhiezer and Berestetskii, 1965). On the other hand, our knowledge about the hadronic cross-sections are based essentially on accelerator data. In the energy region of interest, up to 1015 eV or even higher, all relevant cross-sections are measured with an adequate accuracy for astrophysical applications.
Below we will discuss the properties of the most important absorption and radiation processes in the Y-ray domain with an emphasis on the mechanisms that operate effectively in the high and very high energy regimes, while the processes relevant to low energy domain will be covered briefly.
Two Y-ray production mechanisms related to electron bremsstrahlung and the decay of neutral n-mesons produced at nucleon-nucleon interactions are among the most effective processes resulting in high and very high energy Y-ray emission. The annihilation of positrons, as well as the nuclear processes associated with neutron-capture reactions and de-excitation of nuclei, dominate at lower, MeV energies.
Electron bremsstrahlung and pair-production
Comprehensive analysis of features of the cross-sections of these processes can be found in Heitler (1954) and Akhiezer and Berestetskii (1965). Although the two processes have many similarities, generally electron bremsstrahlung has broader astrophysical applications than pair production. The latter becomes important only in the context of cascade development in optically thick environments.
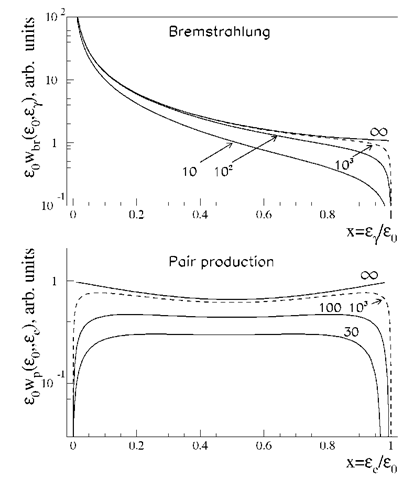
The integral cross-sections of the bremsstrahlung and pair production processes in hydrogen gas are shown in Fig. 3.1. The energies of electrons and Y-rays are expressed in units of mec2. The cross-sections are normalised to the asymptotic value of the pair production cross-section at
where Z is the charge of the target nucleus, and re is the classical electron radius.
Fig. 3.1 Total cross-sections of the bremsstrahlung
and pair production
processes in hydrogen gas normalised to the asymptotic value
of the pair production cross-section at
The bremsstrahlung cross-sections are calculated for secondary
Y-rays produced with energies exceeding (1) the pair-production threshold,
the critical energy,
(3) half of the energy of the primary electron,
This actually implies introduction of the so-called radiation length
the physical meaning of which is the average distance over which the ultra-relativistic electron loses all but 1/e of its energy due to bremsstrahlung. The same parameter also implies the mean free path of Y-rays. This convenient parameter is widely used to describe cascade development in optically thick sources. The cascade effectively develops at depths exceeding the radiation length. Usually the radiation length is expressed in units of g/cm2. For hydrogen gas
The second important parameter that characterises the cascade development is the so-called critical energy below which ionization energy losses dominate over bremsstrahlung losses. In hydrogen gas,
Effective multiplication of particles in a cascade is possible only at energies
At lower energies electrons dissipate their energy by ionization rather than producing more high energy Y-rays which would support further development of the electron-photon shower.
In Fig. 3.1 the bremsstrahlung total cross-sections is calculated for 3 different values of minimum energy of emitted photons:
The first value corresponds to the cross-section of production of all Y-rays capable of producing electron-positron pairs. The second value corresponds to the cross-section for Y-rays produced above the critical energy, and thus capable of supporting the cascade. And finally, the third value corresponds to the cross-section of production of the "most important" Y-rays which play the major role in the cascade development. It is seen from Fig. 3.1 that while for
the pair-production cross-section is an order of magnitude smaller compared to the bremsstrahlung cross-section, for
the cross-sections of two processes become almost identical at
The differential cross-sections of bremsstrahlung and pair production are presented in Fig. 3.2 The pair-production cross section obviously is a symmetric function around the point
The bremsstrahlung differential cross-section has a
type singularity at
, but because of the hard spectrum of bremsstrahlung photons the energy losses of electrons contribute mainly to emission of high energy Y-rays. Thus bremsstrahlung should be treated as an essentially catastrophic process. Nevertheless, it is convenient to introduce the so-called average energy loss-rate,
Correspondingly, the lifetime of electrons due to the bremsstrahlung losses is
where n is the number density of the ambient gas.
Note that the electron energy loss rate given by Eq.(3.3) is proportional to the electron energy, and, correspondingly, the lifetime given by Eq.(3.4) is energy independent. This implies that for a initial (acceleration) power-law spectrum
bremsstrahlung losses do not change the original electron spectrum, taking into account that the cooled steady-state spectrum
is determined as (see e.g. Blumenthal and Gould, 1970)
Fig. 3.2 Differential cross-sections of the bremsstrahlung (upper panel) and pair production (bottom panel) processes in hydrogen. The cross-sections are normalised to one radiation length. The energies of primary electrons and 7-rays
are indicated at the curves.
Interestingly, in the case of power-law spectrum of electrons
the spectrum of bremsstrahlung Y-rays is also power low with the same power-law index (this is a result of
dependence of the differential cross-section). Thus, the bremsstrahlung Y-ray spectrum simply repeats the shape of the electron acceleration spectrum
This is true, however, only when the energy losses are dominated by bremsstrahlung. In hydrogen gas, at energies below
ionization dominates over the bremsstrahlung. Because both the ioniza-tion and bremsstrahlung loss rates are proportional to n, this condition does not depend on the ambient gas density. On the other hand, in the relativistic regime, the ionization loss rate does not depend on the electron energy. Thus, in accordance with Eq.(3.5), the steady-state electron spectrum becomes flatter,
and correspondingly at energies below several hundred MeV we should expect a very hard bremsstrahlung Y-ray spectrum with power-law photon index r — 1.
In many astrophysical scenarios the inverse Compton and synchrotron losses may well dominate, especially at very high energies, over bremsstrahlung, depending on the ratio of the energy density of the radiation and magnetic fields to the number density of the ambient gas. The synchrotron and inverse Compton energy loss rates are proportional to the electron energy. This makes the steady-state electron spectrum steeper, 
and correspondingly the bremsstrahlung Y-rays emerge with photon index r + 1.
Eq.(3.3) and (3.4) are derived for neutral gas. In a fully ionized gas, i.e. in the absence of the screening effect, the corresponding equations are somewhat different (see, e.g., Akhiezer and Berestetskii, 1965). In particular, an additional term proportional to ln ee appears in the energy loss-rate. However these corrections do not essentially change the above conclusions.
Due to ionization losses, the efficiency of bremsstrahlung in the energy range below the critical energy ecr decreases approximately proportional to the electron energy, and becomes very low at sub-relativistic energies. In the nonrelativistic regime, proton bremsstrahlung (often called "inverse" bremsstrahlung) becomes identical to electron bremsstrahlung, when the proton and electron kinetic energies are express in their rest mass units (see e.g. Hayakawa, 1969). Although in some specific cases like in Solar flares, the non-relativistic bremsstrahlung of electrons and protons may play a major role in production of nonthermal X-rays, generally this is a very inefficient radiation mechanism. Because of severe ionization losses only a tiny fraction,
of the kinetic energy of particles is released in X-rays.
Finally we note that since the hard X-rays of energy ex are produced by protons with energy
this process is tightly connected with the prompt Y-ray emission due to excitation of the nuclei of the ambient matter by the same
protons (see Sec.3.1.3.2).
Electron-positron annihilation
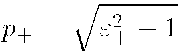
The astrophysical significance of this process,
generally is attributed to the annihilation line at energy
as well as to the 3-photon positronium continuum, produced by annihilation of thermalized positrons with relatively cold thermal electrons of the ambient gas/plasma. However, if the positrons are injected into the production region with relativistic energies, a significant fraction (from 10 to 20 per cent, depending on the ionization state of the ambient plasma) of positrons annihilate in flight before they cool down to the temperature of the thermal background gas.
The differential spectrum of the Y-rays produced in the annihilation of fast positrons with Lorentz-factors
on the ambient electrons with density ne is described by a simple analytical expression.
varies in the limits where the photon energy
varies in the limits
is the dimensionless momentum of the positron.
Here
is the dimensionless momentum of the positron.
For a power-law steady-state spectrum of positrons,
(here r can be interpreted as the primary positron spectral index, assuming that ionization losses make the positron spectrum harder,
the spectrum of annihilation radiation at 
has a power-law form
Thus, the spectrum of annihilation radiation is steeper than the (steady-state) spectrum of the parent positrons, but almost repeats the shape of the primary spectrum of positrons. At lower energies the spectrum has a more complicated form with a broad maximum around 1 MeV.
The total cross-section of annihilation of a relativistic positron of energy 
is given by
Correspondingly the annihilation time is
Comparing Eq.(3.9) with Eq.(3.4) one finds that for positron energies 
the annihilation times becomes shorter than the bremsstrahlung cooling time. This implies that at energies less than approximately 15 MeV the annihilation continuum starts to dominate over the bremsstrahlung spectrum, taking into account that in both processes the leading photon receives a substantial part of the positron kinetic energy.
Gamma rays produced by relativistic protons
-decay gamma rays
This process provides a unique channel of information about the hadronic component of cosmic rays. The important role of this process in gamma-ray astronomy was recognised by the pioneers of the field (see e.g. Ginzburg and Syrovatskii, 1964) long ago.
Relativistic protons and nuclei produce high energy Y-rays in inelastic collisions with ambient gas due to the production and decay of secondary pions, kaons and hyperons. The neutral n0-mesons provide the main channel of conversion of the kinetic energy of protons to high energy Y-rays. For the production of n0-mesons the kinetic energy of protons should exceed
where
is the mass of the
This particle immediately decays to two Y-rays.
The mean lifetime of
is significantly shorter than the lifetime of charged n-mesons
At high energies, all three types of pions are produced with comparable probabilities. The spectral form of n-mesons is generally determined by a few (one or two) leading particles (that carry a significant fraction of the nucleon energy) rather than by the large number of low-energy secondaries.
The decays of charged pions lead to ve and vM neutrinos with spectra quite similar to the spectrum of the accompanying n0-decay Y-rays. However, this symmetry can be violated in environments with high gas or radiation densities. In certain conditions, the characteristic time for inelastic interactions of charged pions with nucleons or photons could be shorter than the decay time, so the energy of pions degrades before they decay. At very high energies this would result in significantly smaller fluxes of neutrinos compared to Y-rays.
The distinct feature of the spectrum of
Y-rays is the maximum at
independent of the energy distribution of 
mesons, and consequently of the parent protons. The appearance of such a bump in the Y-ray spectrum is a result of the
decay kinematics. It is easy to show (see e.g. Stecker, 1971; Ozernoy et al., 1973) that the spectrum of Y-rays from decays of monoenergetic pions of energy En and velocity vn is constantwithin the interval
between
The spectrum of
Y-rays for an arbitrary dis
tribution of
can be presented as superposition of rectangles for which only one point at
is always presented. Obviously this should result in a spectral maximum independent of the distribution of parent pions.
The spectral features of Y-rays through the channel
has been extensively studied by many authors (e.g. Stecker, 1971; Dermer, 1986; Berezinsky et al., 1993; Mori, 1997, etc.). Although precise calculations of Y-ray spectra require quite heavy integrations over differential cross-sections obtained experimentally at particle accelerators, the emissiv-ity of Y-rays for an arbitrary broad energy distribution of protons can be derived within a simple formalism which nevertheless provides surprisingly good accuracy over a broad Y-ray energy range.
The Y-ray emissivity
is directly defined by
as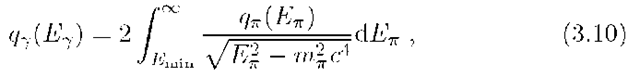 
where
The emissivity of secondary pions qn from inelastic proton-proton interactions can be calculated with high accuracy using accelerator measurements of the inclusive cross-sections
(see e.g. Gaisser, 1990). The emissivity of
: calculated in the function approximation for the cross-section
then becomes
where
is the total cross section of inelastic pp collisions, and
is the mean fraction of the kinetic energy
of the proton transferred to the secondary
is the energy distribution of the protons.
In a broad region from GeV to TeV energies
which includes 
contribution from n meson production (Gaisser 1990). From the threshold at
rapidly to about 30 mb. But after 
increases only logarithmically. In the GeV to TeV energy region, the total cross section can be approximated by
for
with the assumption
at lower energies. More accurate approximations of the cross-section below 1 GeV do not noticeably change the fluxes of Y-rays even at very low energies provided that the broad power-law spectrum of protons extends beyond 10 GeV, and thus the overall flux is contributed to by protons with energies above a few GeV.
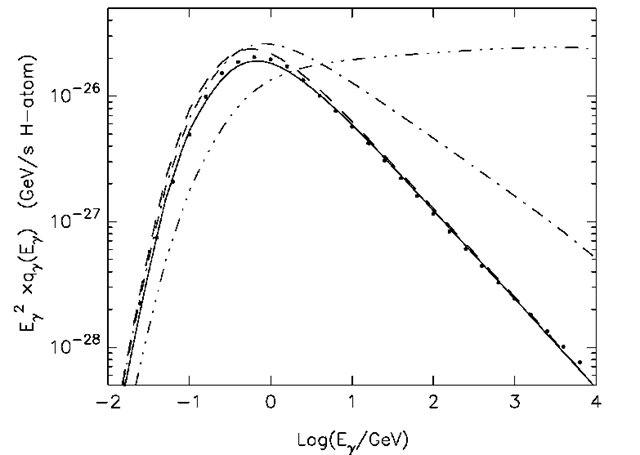
The rather good accuracy of this simple approach is demonstrated in Fig. 3.3 where the emissivity of
Y-rays calculated on the basis of Eq.(3.10) – (3.12) is compared with the results of Monte-Carlo calculations by Mori (1997) based on a detailed treatment of the cross-sections of secondary pion production.
The dashed curve corresponds to a similar calculation but for the local CR proton flux given in the form of Eq. (4.30),which has been used for the detailed Y-ray emissivity calculations by Dermer (1986) (the original spectrum from Dermer (1986) is not shown in order not to overload the figure with almost coinciding curves). The two other curves in Fig. 3.3 correspond to the emissivities calculated for power law proton spectra with spectral indices r = 2.5 (dot-dashed curve) and r = 2 (3-dot-dashed curve), normalised to the same energy density of CR protons
derived from the CR proton flux given by Eq. (4.30). For CR proton spectra with
the emissivities, in terms of
reach their maximum at
and then at lower energies the spectra sharply decline.
The characteristic cooling time of relativistic protons due to inelastic p-p interactions in the hydrogen medium with number density n0 is almost independent of energy. Assuming an average cross-section at very high energies of about 40 mb (see Eq.(3.12)), and taking into account that on average the proton loses about half of its energy per interaction (for the coefficient of inelasticity
we find
Since the tpp cooling time is almost energy-independent in the energy region above 1 GeV, where the nuclear losses well dominate over ionization losses, the initial (acceleration) spectrum of protons remains unchanged. On the other hand, the Y-ray spectrum essentially repeats the spectrum of the parent protons. This implies that at high energies Y-rays carry direct information about the acceleration spectrum of protons. To a certain extent, this is similar to the bremsstrahlung Y-rays of relativistic electrons.
Assuming that the electrons and protons are accelerated with the same power-law spectrum, the ratio of Y-ray emissivities of these two processes can be estimated as
where r is the electron to proton ratio. Thus for
(which is the case for the galactic cosmic rays), the
at high energies dominates over the bremsstrahlung Y-rays. Moreover, at very high energies, due to inverse Compton and synchrotron losses, the contribution from electron bremsstrahlung is further suppressed.
Fig. 3.3 The emissivities, per 1 H-atom, of
7-rays calculated using an approximate method given by Eq. (3.10)-(3.12) for the spectra of CR protons corresponding to the ‘median’ proton flux (solid line) of Mori (1997), and the flux given by Eq. (4.30) (dashed line), as compared with the results of detailed calculations by Mori (1997) shown by full dots. The dot-dashed and 3-dot—dashed curves correspond to the emissivities calculated for the single power-law spectra of protons with indices
Nuclear gamma-ray line emission
Although below 300 MeV the protons cannot produce pions, they still play an important role in the production of Y-rays through nuclear excitation of the ambient medium (Ramaty et al., 1979). De-excitation of the target nuclei leads to Y-ray lines in the energy region between several hundred keV to several MeV. The excitation cross-sections for the isotopes most relevant for astrophysical applications have been recently comprehensively reviewed by Kozlovsky et al. (2002). The energy region of nonthermal particles responsible for the prompt Y-ray line emission, extends approximately from several MeV to 100 MeV per nucleon. The Y-ray emission is formed by contributions from both target and projectile nuclei. The lines from both components are broad. In the first case the typical line width in the cold, low density medium is of the order of several tens of keV; it is determined essentially by the recoil momentum of the target nucleus. The Y-ray lines from projectile nuclei are broader due to their high velocities, 0.1c or more. Apart from these broad line components, one would expect also very narrow Y-ray lines, if the target nuclei are contained in cosmic grains. In this case, because of ionization losses, the excited nuclei come to the rest before they decay.
The spectrum of de-excitation Y-ray line emission depends on the abundance of elements in cosmic rays (very broad lines) and in the ambient medium both in the form of the gaseous component (broad lines) and grains (narrow lines). The most distinct features in the overall nuclear Y-ray spectrum appear around 4.4 MeV (from 12C*), 6.1 MeV (from 16O*), 0.85 MeV (56Fe*), 0.45 MeV (from a-a reactions), etc.
Generally, the formation of nuclear Y-ray emission through excitation of nuclei by low energy (sub-relativistic) cosmic rays is quite an inefficient mechanism in the sense that only a very small fraction, 10-5 to 10-6 of the kinetic energy of fast particles is released in the form Y-ray lines.The rest goes to the heating and ionization of the ambient gas. The problem of ionization or, in the fully ionized plasma, Coulomb losses can be somewhat relaxed, assuming that Y-ray production takes place in a hot two temperature plasma with
However, the nuclear de-excitation line production efficiency in such environment remains rather small. Indeed, in a plasma with an ion temperature high enough for nuclear excitation, inelastic spallation reactions proceed at a similar or higher rate, leading to nuclear destruction during the time equal or smaller to the stationary high-temperature plasma formation time. As a result, the nuclear line luminosity cannot exceed 10-4 of the total luminosity radiated away by the electron component.
An interesting outcome of the spallation reactions in compact objects is the formation of a proton-neutron plasma without a noticeable content of nuclei, but, due to electro-neutrality, with electrons and, possibly, positrons. In addition, if the plasma density is sufficiently high,
(thus the neutrons are effectively captured by protons before they decay), deuterium nuclei co-exist in equilibrium with protons and neutrons. Because of rapid radiative cooling of electrons through the thermal bremsstrahlung and/or Comptonization, a two temperature plasma can be formed around a black hole in which the nucleons lose their energy mainly through p-e Coulomb exchange. Besides, the nucleons radiatively cool due to the capture of neutrons by protons and proton-neutron bremsstrahlung.Although the energy spectra of these two radiation components are different, the peak luminosities of both processes appear in the Y-ray domain,
At temperatures
the pion production becomes an additional Y-ray production channel, concerning the low efficiency of this process, at least in spherical accretion flow).
Observations of Y-rays with characteristic spectra in the 1 to 100 MeV energy range can provide direct evidence of the formation of two temperature plasmas under conditions when the heavy nuclei are destroyed, and the emission in Y-ray lines is suppressed. Another interesting effect connected with such a scenario is the escape ("evaporation") of neutrons from the accretion flow, and their capture by the atmosphere of the companion star.In dense cold regions, the neutrons are quickly thermalized and captured by protons resulting in narrow 2.22 MeV Y-ray line emission. Moreover, it has been shown (Belyanin and Derishev, 2001) that for a broad range of accretion parameters, neutrons may effectively decouple from protons leading to the formation of a self-sustained halo. This implies that new neutrons in the halo are supplied mainly by the destruction of helium nuclei by the existing neutrons. Thus, once formed, such a halo can exist even if the proton temperature is much lower than the energy threshold of helium dissociation.
Finally we note that Y-ray line emission is expected also from radioactive isotopes synthesised in stellar interiors or during supernova explosions (Clayton, 1982). Since nucleosynthesis can be effective only in very dense environments, of the large number of Y-ray lines only a few can survive and be observed. These are Y-rays related to the abundant isotopes with long lifetimes. The best candidates are lines from 26Al and 60Fe for the production of diffuse galactic emission, as well as Y-ray lines from 7Be, 44 Ti and 56 Ni that can observed during solitary transient phenomena (see, for a review, e.g. Diehl and Timmes, 1998; Tatischeff, 2002).
