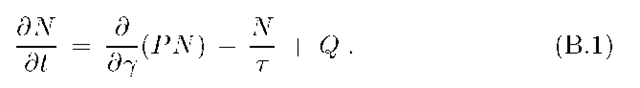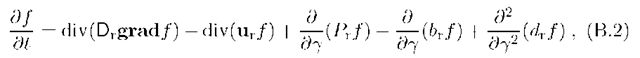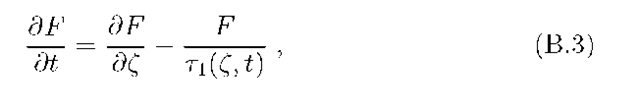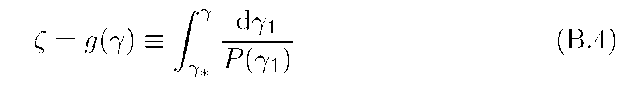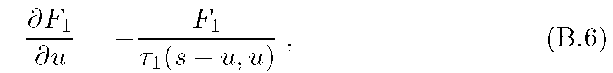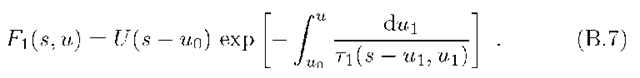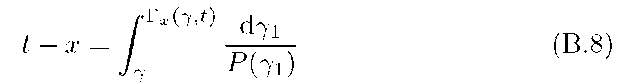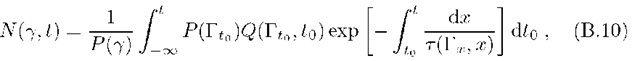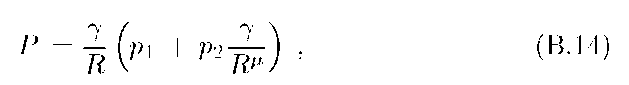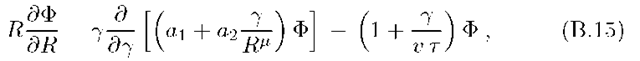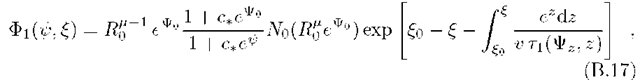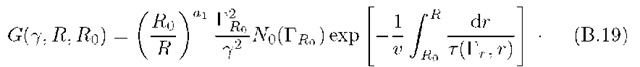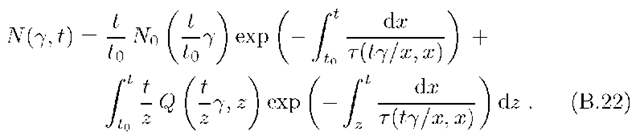Kinetic equation
The formalism described below was developed by Atoyan (1999) to study the time evolution of the energy distribution of relativis-tic electrons in an expanding magnetised medium for an arbitrary time-dependent injection rate, taking into account both adiabatic and radiative energy losses, as well as losses caused by the energy- and time-dependent escape of electrons. The results of this convenient analytical approach can be applied to the study of the nonthermal radiation components of relativistic jets in AGN and microquasars.
The kinetic equation describing the evolution of the energy distribution function of relativistic electrons in a spatially homogeneous source N = N(y, t) is the well known partial differential equation (e.g. Ginzburg and Sirovatskii, 1964):
The Green’s function solution to this equation in the case of time-independent energy losses and constant escape time
was found by Syrovatskii (1959). However, in an expanding magnetised cloud under consideration we have to suppose that all parameters depend on both energy Y and time t, i.e.
is the injection spectrum,
is characteristic escape time of a particle from the source, and 
is the energy loss rate.
Strictly speaking, Eq.(B.1) corresponds to a spatially homogeneous source where the energy gain due to in-situ acceleration of particles is absent. Actually, however, it may have wider applications. Indeed, in a general form the equation describing the evolution of the local energy distribution function
of relativistic particles can be written (e.g. Ginzburg and Syrovatskii, 1964) as:
where all parameters depend also on the radius-vector r. The first two terms on the right-hand side of this equation describe the diffusive and convective propagation of particles, and the last two terms correspond to the acceleration of the particles through the first and second order Fermi mechanisms. If there are internal sources and sinks of particle injection (such as production and annihilation), then terms similar to the last two in Eq.(B.1) should be added as well.
Let us consider a source where the region of effective particle acceleration can be separated from the main emission region. This is likely to be the case of blobs in blazars and microquasars, where the probable site for in-situ acceleration of electrons is a relatively thin region around either the bow shock front formed ahead of the cloud, or possibly a jet termination shock formed behind the cloud. Meanwhile the main part of the observed flux should be produced in a much larger volume, V0, of the post-shock region in the cloud, since the synchrotron cooling time of radio electrons is orders of magnitude larger than the dynamical times of the source. Since the acceleration efficiency (parameters br and dr) should drop significantly outside the shock region, after integration of Eq.(B.2) over the volume V0 the last two terms can be neglected.
The integration of the left side of Eq.(B.2) results exactly in dN/dt. Integration of the two propagation terms in the right side of Eq.(B.2) gives the net flux of particles, due to diffusion and convection, across the surface of the emission region. Obviously, these terms are expressed as the difference between the total numbers of particles injected into and escaping from the volume V0 per unit time, so the last two terms of Eq.(B.1) are found (internal sources and sinks, if present, are also implied). Finally, integration of the energy loss term in Eq.(B.2) is reduced to the relevant term of Eq.(B.1), where P corresponds to the mean energy loss rate per particle of energy 7, i.e.
The volume V0 of the cloud implies the region filled with relativistic electrons and enhanced magnetic field, where the bulk of the observed radiation is produced.
Thus, Eq.(B.1) is quite applicable to the study of sources with ongoing in-situ acceleration, as long as the volume V0, where the bulk of nonthermal radiation is produced, is much larger than the volume AV of the region(s) in the source responsible for the effective acceleration of the electrons. Note that solutions for a large number of particular cases of the Fokker-Planck partial differential equation (which includes the term <x Jr for stochastic acceleration), corresponding to different combinations of terms responsible for time-dependent adiabatic and synchrotron energy losses, stochastic and regular acceleration, were obtained long ago and have been qualitatively discussed by Kardashev (1962), assuming energy-independent escape of relativistic particles from the production region. However, in the jets of microquasars, and perhaps also blazars, the energy-dependent escape of electrons from the active zone may play an important role in spectral evolution of the resulting synchrotron and inverse Compton emission. Another important point is that the Fokker-Planck equation generally may contain a singularity, so transition from the solutions of that equation (if known), which are mostly expressed through special functions, to the case of dr ^ 0 may not always be straightforward (for a comprehensive discussion of the problems related with singularities in the Fokker-Planck equation, as well as general solutions for time-independent parameters see Park and Petrosian (1995), and references therein). Meanwhile, substitution of the acceleration terms by effective injection terms in the regions responsible for the bulk of nonthermal radiation, allows us to disentangle the problems of acceleration and emission of the electrons, and enables analytical solutions to the first order equation Eq.(B.1) which are convenient both for further qualitative analysis and numerical calculations.
Time-independent energy losses
Suppose first that the escape time is given as
but the energy losses are time-independent,
The Green’s function solution
for an arbitrary injection spectrum
of electrons implies J-functional injection
at some instant t0. At times
it actually corresponds to the solution for the homogeneous part of Eq.(B.1), with initial condition
Then for the function F = PG this equation is reduced to the form
where instead of the energy Y, a new variable is introduced,
where 7* is some fixed energy. Formally, Z has the meaning of the time needed for a particle with energy 7 to cool to energy 7* (so for convenience one may suppose 7* = 1). The function
where e is the inverse function of 3(7) which expresses the energy through
The initial condition for
reads
Transformation of Eq.(B.3) from variables
results in a partial differential equation over only one variable for the function 
with the initial condition
found from Eq.(B.5). Integration of Eq.(B.6) is straightforward:
In order to return from variables
it is useful to understand the meaning of the function
which enters into Eq.(B.7) via Eq.(B.5) for U and the escape function
Since e is the inverse function of g, then for any z in the range of definition of this function,
Then, taking into account that
one obtains
For the function g defined by Eq.(B.4), this equation results in
where
corresponds to
after its transformation to the variables (7, t). Thus, for a particle with energy 7 at an instant t, the function 
is the energy
of that particle at time x, i.e. it describes the trajectory of individual particles in energy space.
Expressing Eq.(B.7) in terms of the Green’s function G = F/P, the solution to Eq.(B.1) for an arbitrary t(7,t), but with time-independent energy losses, is found:
Note that this is not a standard Green’s function in the sense that the injection spectrum was supposed as an arbitrary function of energy N0(y), and not necessarily a delta-function. Actually, it describes the evolution of relativistic particles with a given distribution
The solution for an arbitrary continuous injection spectrum is readily found after substitution
into Eq.(B.9) and integration over d to:
with the function r defined via Eq.(B.8). In the particular case of time and energy independent escape,
this solution coincides with the one given in Syrovatskii (1959) in the form of double integral over t0 and r, if Eq.(B.10) is integrated over energy with the use of general relations
which follow from Eq.(B.8).
Some specific cases of Eq.(B.10) are worth brief discussion. Let the escape of particles be energy dependent but stationary,
and consider first the evolution of
when energy losses are negligible, so
for any t. Assuming for convenience that the form of injection spectrum does not change in time, i.e.
0 (i.e. injection starts at t=0), Eq.(B.10) is reduced to
For stationary injection
the integral results in the simple
and then the escape of
electrons modifies the particle distribution, compared with the injection spectrum, as
In the case of
it results in a power-law steepening of the injection spectrum by factor of
This is the well known result of the so-called leaky-box model in cosmic ray theory. In the case of non-stationary injection, however, the modification of Q(y) is different. In particular, for an impulsive injection,
it is reduced to a sharp cut-off of an exponential type above energies Yt found from
For a stationary injection of particles, Eq.(B.10) can be transformed to the form
using Eq.(B.11). In the case of
(absence of escape) and large t, when
comes to the familiar steady state solution for distribution of particles in an infinite medium. If the synchrotron (or IC) energy losses of electrons dominate,
In this case
and then the radiative losses result in a quick steepening of a stationary power-law injection spectrum by a factor of 1. Meanwhile, in the case of impulsive injection the modification of the initial spectrum of electrons is reduced to an exponential cut-off at 
(see Kardashev, 1962).
Expanding cloud
Energy losses of relativistic electrons in an expanding medium become time-dependent. The adiabatic energy loss rate is given as
where
R is the characteristic radius of the source, and v is the speed of spherical expansion. For electrons of higher energies, however, synchrotron losses may dominate. For the magnetic field we suppose a power-law dependence, 
where B0 and R0 are the magnetic field and the radius of the cloud at instant t0. Thus,
where
For adiabatic losses, pi = v, but the constants pi and p2 are kept in parametric form in order to enable other losses with similar dependence on 7 and R as well. Here we will suppose that the expansion speed v = const, and consider evolution of the particles injected impulsively at instant t0 with the spectrum
as previously.
Since the energy losses depend on time via the radius
t0), it is convenient to pass from the variable t to R. Then, for the function
reads:
where
and for t now we imply the function
Transformation of this equation from variables
in
results in the equation
where
The initial condition
at
Thus, we come to the equation formally coinciding with the one considered above, with ‘time’ (£) independent ‘energy’
and arbitrary ‘escape’ function
The solution to this equation is analogous to Eq.(B.9) :
where
is the characteristic trajectory of a particle in the ‘energy’ space —, which is readily calculated from Eq.(B.8) for the given P*:
where
is the characteristic trajectory of a particle in the ‘energy’ space —, which is readily calculated from Eq.(B.8) for the given P*:
Returning now to the variables Y and R, the evolution of particles can be described by the function
The energy
corresponds to the trajectory of a particle with given energy
in the (r, r) plane, and can be represented as
where
In the formal case of
tends to the limit
In the general case of continuous injection of relativistic particles with the rate
the evolution of their energy distribution during expansion of the cloud between radii
is found, using Eq.(B.19):
Here
is given by Eq.(B.19). The substitution
results in an explicit expression for N(7, t). If the source is expanding with a constant velocity v starting from t = 0, such a substitution results in formal changes
. When only the adiabatic losses are important, i.e
is reduced to a simple
and
For the energy-independent escape,
, a similar equation can be obtained from the relevant Green’s function solution found by Kardashev (1962) for the case of "stochastic acceleration + adiabatic losses + leakage", if the acceleration parameter tends to zero.
It is seen from Eq.(B.22) that for a power-injection
with
the contribution of the first term quickly decreases, so at
only the contribution due to continuous injection is important. This term is easily integrated assuming stationary injection and approximating t =
In the case of
the energy distribution
of electrons at
similar to the case of a non-expanding source. If
the condition
can be satisfied only for sufficiently large Y, so only at these energies can the energy-dependent escape of particles from an expanding cloud result in a steepening of
Although Eq.(B.22) is derived under the assumption of a constant expansion speed v, it can be readily used in the numerical calculations for any profile of v(t), by approximating the latter in the form of step functions with different mean speeds V; in the succession of intervals (t;,ti+i).
