Nondeterministic Finite-State Acceptors
Nondeterministic finite-state acceptors (NFA), or nondeterministic finite automata, are similar to deterministic finite-state acceptors except that there may be more than one possible state that is attainable from a given state for the same input character.
Table 4-1
|
State |
|
Input |
|
0 |
1 |
|
|
S |
B |
A |
|
A |
C |
S |
|
B |
S |
C |
|
C |
A |
B |
Table 4-2 Traces of two strings using the DFA
|
Input string |
||
|
110101 |
|
11101 |
|
M(S, 110101) = A/(/U0101) |
M(S,11101) = M(A,1101) |
|
|
= M(S, 0101) |
= Af(5,101) |
|
|
= A/(fl,101) |
= M(A,01) |
|
|
= M(C, 01) |
= M(C, 1) |
|
|
= M(A, 1) |
= M(B,e) |
|
|
= M(S, e) |
= B (reject) |
|
|
= S (accept) |
||
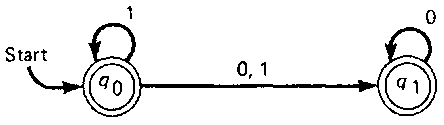
Thus an ambiguity seems to arise because the acceptor has several possibilities to choose from. However, the acceptor is considered to explore all possibilities, one at a time, to determine if a string should be accepted. Consider the NFA given in Fig. 4-6 which accepts strings of the form amb" where m, n > 1. A string will be accepted by the NFA if at least one valid sequence of state transitions exists such that the acceptor is in a final state when the entire string has been read. From the finite-state diagram, it should be observed that in order for the acceptor to accept a string if possible, it stays in state A until the final character a is read. The acceptor then changes to state B. Similarly, the NFA stays in state B until the final character b is read, causing a transition to state C.
Definition 4-3 A nondeterministic finite-state acceptor is a 5-tuple (K, VT, M, S, Z) where:
A" is a finite, nonempty set of states.
VT is an input alphabet.
M is a mapping of K X VT into subsets of![]()
![]() is the starting state,
is the starting state, ![]() is the set of final states.
is the set of final states.
Notice that the mapping function M is similar to that for a DFA except that M maps into a possibly empty set of states. Hence we write M(Q,T) = {Px, P2,…, Pn} where a transition from state Q to one of the states Px, P2,…,P„ occurs when a character T from VT is read. The mapping function for an NFA is extended with the following definitions:
Figure 4-6 An example of a nondeterministic finite-state acceptor.
The first definition implies that for the empty string, the acceptor must stay in the same state. The meaning of the second definition is less obvious. If M(Q, T) = {Px, P2,.. -, P„], then the second definition can be written as M(Q,Tt) =
![]() Thus, M(Q,Tt) is the set of all possible states that the acceptor may end up in after the string Tt has been read. The third definition extends the mapping function to
Thus, M(Q,Tt) is the set of all possible states that the acceptor may end up in after the string Tt has been read. The third definition extends the mapping function to![]() and defines the mapping to be the union of all the sets resulting from applying each individual state from the set of states to the string x.
and defines the mapping to be the union of all the sets resulting from applying each individual state from the set of states to the string x.
A string x is said to be accepted by an NFA if at least one of the states attainable from the starting state by reading x is a final state; that is, x is accepted by the NFA F = (K, VT, M, S, Z) if for some state![]() then
then
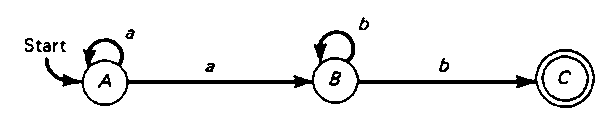
As an example of an NFA, consider a machine which accepts the set of strings in {a,b,c}* such that the last symbol in the input string also appears earlier in the string. For example, bab is accepted but cbbca is not. The finite-state diagram for this acceptor is given in Fig. 4-7. For M as defined in Table 4-3, the acceptor is given as
With the input string aca, the value of M(q0, aca) can be determined as follows:
Table 4-3 Transition table for a nondeterministic finite-state acceptor
|
State |
|
Input symbol |
|
|
a |
. h |
c |
|
Figure 4-7 Transition diagram for a nondeterministic finite-state acceptor.
Now
so
Hence
and since![]() the string aca is accepted.
the string aca is accepted.
It should be emphasized that although a nondeterministic machine does not have unique moves, it does not contain a random device for choosing its move. Rather, the acceptor explores all possible move sequences, and if at least one of these sequences leads to a final state, then the input string is accepted.
While it might seem likely that nondeterministic finite-state acceptors are more powerful than deterministic acceptors, the following theorem proves that such is not the case. The theorem also provides a method for converting an NFA to a DFA.
Theorem 4-1 Let![]() be a nondeterministic finite-state acceptor accepting a set of strings L. Define a DFA
be a nondeterministic finite-state acceptor accepting a set of strings L. Define a DFA![]() as follows:
as follows:
1. The alphabet of states consists of all the subsets of K. An element of K’ is denoted as [S1( S2,..., S1,], where Sv S2,…,SI are states of K. The states Sx, S2,…,SI are in the same canonical order, so that for some states in K, {S1,S2}(= {S2,S,}) is always S2].
2. The set of input characters VT is the same for F and F’.
3. The mapping M’ is defined as
where
4. If the starting state of F is S„ then S’ = [5,].
5. Z’ is the set of all states in K’ containing a final state in Z.
Then the set of strings accepted by F’ is the same as that for F.
Proof It must be shown that L(F’) = L(F) with the construction given in the theorem. Thus it is necessary to show that M’(S’, x) = P2,…, PJ is equivalent to M(S, x) = {Pv P2,…, P,}. This can be done by induction on the length of the string x. The result is trivial for |x| = 0, since x = e and S’ = [S] from the mapping M(S,e)= {5}.
Assume that M’(S’,x) is equivalent to M(S,x) for![]() Then for
Then for
By the inductive hypothesis
is equivalent to
By definition, we have
is equivalent to
Thus the equivalence holds for
and
Thus the equivalence holds for
is equivalent to
Thus
The construction given in the theorem may be applied to any NFA. For example, the NFA![]() where the mapping
where the mapping
function is defined in Table 4-4, can be converted to a DFA as follows: Define
![]() where VT is the same as for F and the starting state is
where VT is the same as for F and the starting state is ![]() The states of K’ are initially defined as
The states of K’ are initially defined as![]() and the mapping M’ is readily obtained from the transition table for F. The mapping of these states is
and the mapping M’ is readily obtained from the transition table for F. The mapping of these states is
A new state
is created and from the mapping of F
the mapping M’ is defined as
Similarly, the new state [<7lt q2] is added to K’ and the mappings
are defined. As no new states were created with the last mapping definitions, the creation of the DFA is nearly complete. The set of final states of F’, which is all that is left to be defined, are those states of K’ which contain an element of Z. In this example,
The notion of a nondeterministic finite-state acceptor is extended to include state transitions with the empty string as input in the next subsection. The next subsection also shews that such an acceptor is no more powerful than an acceptor which cannot change state when reading the empty string.
Nondeterministic Finite-State Acceptors with e-Transitions
In this subsection, nondeterministic finite-state acceptors are allowed to have state transitions with the empty string used as input. As might be expected, such an acceptor is no more powerful than the finite-state acceptors introduced in the previous subsections.
Table 4-4
|
State |
|
Input |
|
a |
b |
|
Figure 4-8 A nondeterministic finite-state acceptor with f-transitions
Rather, it is a convenient construct for representing regular expressions.
The transition diagram for an NFA with e-transitions is given in Fig. 4-8. This machine accepts strings of the form 1"’0" where m, n > 0. After reading a sequence of Is from the input string, the acceptor changes to state q{, before reading the 0s which follow. This is done by reading the empty string which is found between the last 1 and the first 0.
Definition 4-4 A nondeterministic finite-state acceptor with e-transitions is a 5-tuple (K,Vt,M,S,Z), where K, VT, S, and Z are the same as in Definition 4-3 and M is the mapping![]() into subsets of K.
into subsets of K.
Using this definition, the NFA depicted in Fig. 4-8 can be defined as
![]() with the mapping function defined by Table 4-5.
with the mapping function defined by Table 4-5.
Before the equivalence of an NFA with e-transitions and an NFA without e-transitions can be proved, it is necessary to define e-transitions and define the mapping function for M(q,x) where .![]()
Definition 4-5 e-CLOSURE is a set of states of an NFA with e-transitions, say F, such that e-CLOSURE for some state of F, call it q, includes all states attainable from that state by making state transitions with e-transitions. This is denoted by e-CLOSURE(^).
In the example of Fig. 4-8,![]() and
and![]()
![]() Notice that
Notice that![]() for some state q invariably includes that state because a state can always be thought of as having an e-transition to itself. Furthermore,
for some state q invariably includes that state because a state can always be thought of as having an e-transition to itself. Furthermore,![]() for a set of states P. The definition of
for a set of states P. The definition of![]() allows the mapping function to be extended with the definitions:
allows the mapping function to be extended with the definitions:
Table 4-5
|
|
Input |
|
|
|
State |
0 |
1 |
E |
The first definition states what the mapping of a state to a set of siates is when the empty string is read. In the second case, the mapping K X is defined, allowing the application of the mapping function to include strings.
It is now possible to show the equivalence of NFAs with e-transitions to those without. The proof of the following theorem gives the method for constructing an NFA without e-transitions.
Theorem 4-2 Define![]() as an NFA with e-transitions.
as an NFA with e-transitions.
Then there exists an NFA F’ without e-transitions such that L(F) = L(F’). In other words, the languages accepted by the two acceptors are the same.
Proof Define an NFA F’ without e-transitions as![]() where K, VT, and S are the same as for F and
where K, VT, and S are the same as for F and
and M’(q,a) is M(q,a) for![]() where M is the mapping function M of F extended to strings. By induction on |x| it is necessary to show that
where M is the mapping function M of F extended to strings. By induction on |x| it is necessary to show that![]() . Trivially if
. Trivially if![]() then
then![]() S and
S and![]() if a final state is
if a final state is
The inductive step is as follows. Assume![]() and
and![]() Then
Then
We must show that M’(S, x) contains a final state if and only if M(S,x) contains a final state. It was previously shown that such is the case of x = e. Consider![]() By the construction of F’, if
By the construction of F’, if
Table 4-6
|
Input |
|
|
State |
0 1 |
Figure 4-9
M(S, x) contains a final state, then so does M’(S. x). We must also show the converse; that is, M(S,x) contains a final state if M’(S,x) also does. Consider M’(S,x) containing a state of Z’ other than S. Then M(S,x) must contain a corresponding final state, say, Z. This comes from the construction of F’. Furthermore, if![]() then we have a state in
then we have a state in ![]() and F also in M(S, x) because
and F also in M(S, x) because![]()
Using the construction from the proof given above, an NFA without e-transitions can be constructed from the NFA given near the beginning of this subsection. The acceptor![]() I has its mapping function as defined in Table 4-6. The transition diagram for F’ is given in Fig. 4-9.
I has its mapping function as defined in Table 4-6. The transition diagram for F’ is given in Fig. 4-9.
This section has introduced three types of finite-state acceptors with each new acceptor appearing to be more powerful than the previous one. It was proven that the languages which can be accepted by each acceptor were the same, however. The next two sections demonstrate the equivalence of regular grammars and regular expressions to finite-state acceptors. Methods to convert from a regular grammar or a regular expression to a finite-state acceptor and vice versa are also described.
![tmp4C8-169_thumb[2][2] tmp4C8-169_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8169_thumb22_thumb.png)
![tmp4C8-179_thumb[2][2] tmp4C8-179_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8179_thumb22_thumb.png)

![tmp4C8-201_thumb[2][2] tmp4C8-201_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8201_thumb22_thumb.png)
![tmp4C8-202_thumb[2][2] tmp4C8-202_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8202_thumb22_thumb.png)
![tmp4C8-203_thumb[2][2] tmp4C8-203_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8203_thumb22_thumb.png)
![tmp4C8-214_thumb[2][2] tmp4C8-214_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8214_thumb22_thumb.png)
![tmp4C8-216_thumb[2][2] tmp4C8-216_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8216_thumb22_thumb.png)
![tmp4C8-217_thumb[2][2] tmp4C8-217_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8217_thumb22_thumb.png)
![tmp4C8-222_thumb[2][2] tmp4C8-222_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8222_thumb22_thumb.png)
![tmp4C8-231_thumb[2][2] tmp4C8-231_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8231_thumb22_thumb.png)
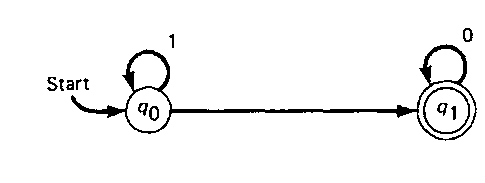
![tmp4C8-273_thumb[2][2] tmp4C8-273_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8273_thumb22_thumb.png)
![tmp4C8-278_thumb[2][2] tmp4C8-278_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8278_thumb22_thumb.png)
![tmp4C8-296_thumb[2][2] tmp4C8-296_thumb[2][2]](http://what-when-how.com/wp-content/uploads/2011/08/tmp4C8296_thumb22_thumb.png)