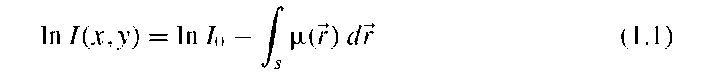A number of fundamentally different methods of obtaining images from tissue, called imaging modalities, emerged during the historical development of biomedical imaging, and the information that these modalities provide differs among modalities.
It is outside our scope here to provide a detailed description of the physical and engineering foundations of the modalities, but a short overview is provided for completeness.
X-ray Imaging X-ray imaging is a projection method. The patient is illuminated by x-rays, high-energy photons that penetrate the body. Some of the x-rays are absorbed in the tissue. X-rays predominantly follow a straight path. The absorption process can be described by the Lambert-Beer law:
where I is the x-ray intensity that passes through a patient’s body, I0 the incident x-ray intensity, ^(r) the x-ray absorption coefficient at any spatial location r, and the integration takes place along a straight line s, which intersects with the x-ray film at (x,y). At this location, the film is blackened by the x-rays, and the more x-rays that pass through the body, the higher the optical density of the film. At the end of this process, the film contains a two-dimensional distribution of optical density that relates to the tissue distribution inside the patient. If path s passes through bone, for example, the optical density at the end of that path is lower than that of a neighboring path, s’, that traverses only soft tissue. In the case of film-based x-ray imaging, the film needs to be digitized with a film scanner to obtain a digital image. Filmless x-ray imaging with a digital detector is becoming more common.
Computed Tomography Computed tomography (CT) is an x-ray-based imaging method used to obtain a two- or three-dimensional map of absorbers inside the imaged object. The principle behind CT is to collect many projections, following equation (1.1), at various angles 0 relative to the imaged object. One projection consists of measured attenuation values along parallel beams that are displaced a distance t from the center of rotation. When the incident beam intensity is known, the line integral along s can be represented by the computed attenuation p at detector position t and angle 0. Let us assume that the Fourier transform of the absorption map ^(x,y) is M(u,v) = F {^(x,y)}, where the symbol F denotes the Fourier transform and u and v are the axes of the frequency-domain coordinate system (a detailed explanation is provided in topic 3). It can be shown that the one-dimensional Fourier transform of the projection with respect to t, F{p(t,0)}, is identical to a one-dimensional cross section of the Fourier transform of the absorber map M(u,v) subtending an angle 0 with the u-axis. This relationship is known as the Fourier slice theorem. In CT, the projections p(t,0) are obtained during the scanning process, but the absorption map ^(x,y) is unknown. The purpose of the scanning process is therefore to obtain many projection scans p(t,0), to perform a Fourier transform, and to enter them at the angle 0 into a placeholder M(u,v), thereby filling as many elements of M(u,v) as possible. The cross-sectional slice ^(x,y) is then obtained by computing the inverse Fourier transform of M(u,v). Other reconstruction methods also exist (a comprehensive overview of CT reconstruction techniques is presented by Kak and Slaney42), as well as reconstruction algorithms for beams that are not parallel but fan- or cone-shaped. To obtain projections at different angles, a CT scanner contains an x-ray source and a detector array mounted on opposite sides of a large ring (the gantry). The patient is placed in the center of the ring and the source-detector system rotates around the patient, collecting projections. The patient can be moved in the axial direction on a patient tray. The patient tray not only allows patient positioning but also the acquisition of three-dimensional images.
Magnetic Resonance Imaging Magnetic resonance imaging (MRI) is another modality that requires the use of a computer for image formation. In a strong magnetic field, protons orient their spins along the magnetic field. The magnetic moments are not perfectly aligned, but rather, precess around the external field lines with an angular frequency that is proportional to the external field. The precession frequency is known as the Larmor frequency. With an externally introduced radio-frequency (RF) signal in resonance, that is, at the Larmor frequency, the orientation of the electron spins can be manipulated, but after cessation of the RF signal, the spins return to their original position. During this process, the spins emit a weak RF signal (echo) that can be picked up by an antenna. The time is takes for the spins to return to their original position depends on the tissue. Magnetic gradients allow us to change the precession frequency and precession phase angle along the spatial axes, and the spatial origin of a RF echo component can be reconstructed by Fourier analysis of the signal. In fact, the task of any MRI pulse sequence (i.e., the sequence of RF signals that manipulates spin precession) is to fill a frequency-domain placeholder, called a k-space matrix, with data. Inverse Fourier transform of the k-space matrix yields the cross-sectional image. Depending on the pulse sequence, different information can be obtained from the tissue. Three tissue constants are the relaxation times T1 and T2 and the proton density (water content). These tissue constants can vary strongly between different types of soft tissue, and for this reason, MRI provides excellent tissue-tissue contrast.
Ultrasound Imaging Ultrasound imaging makes use of the physics of sound propagation in tissue. Sound waves propagate at a certain, tissue-dependent velocity. At the interface between two tissues, some of the sound is reflected, and the sound echo can be picked up by a receiver. The round-trip time of the echo can be translated into the depth of the echo source because the speed of sound is known. An A-mode scan (the echo strength as a function of depth) is obtained by emitting a short burst of sound into the tissue and recording the echos for a short period of time. Sound generation and recording are carried out by transducers made of a piezoelectric material, that is, crystals that deform under the influence of an electric field and that generate an electrostatic field when deformed. An A-mode scan can be represented as a thin line on a screen where the intensity depends on the echo strength. By directing the incident sound wave in different directions, a B-mode scan can be obtained. A B-mode scan consists of several parallel or fan-shaped A-mode scans. It is also possible to record A-mode scans as a function of time, which is referred to as an M-mode (motion mode). Although ultrasound imaging could be performed with purely analog circuits, today’s ultrasound devices use digital signal and image processing. One disadvantage of ultrasound imaging is its widely qualitative nature, although size measurements are possible with moderate accuracy. However, ultrasound can quantitatively measure motion (notably, blood flow) through the Doppler effect.
Single-Photon Emission Computed Tomography (SPECT) SPECT is analogous to CT but uses a radiation source internal to a patient rather than the external x-ray generator used in CT. The radiation source is usually a radiopharmaceutical that emits gamma rays. External cameras obtain projections of the radiation strength analogous to the projection p(t,0) in CT. Radiation is kept weak, and highly sensitive cameras need to be used to capture as many radioactive events as possible. Since the radioactive events are random processes, the image has a very high noise component. Therefore, SPECT image reconstruction methods are optimized for noisy images. Furthermore, the resolution is much lower than that of CT. However, SPECT allows us to image the accumulation of radioactive tracers at physiologically active sites. Whereas CT provides information about the structure of tissue, SPECT provides information about function and physiological activity.
Positron Emission Tomography (PET) Like SPECT, PET uses radiolabeled markers to image physiological activity. Whereas SPECT uses primarily gamma emitters, the radiolabeled compounds in PET are positron emitters (such as 18F, 150,124I, and 89Zr). The positron (i.e., antimatter electron) collides with an electron a short distance from its emission site. In this annihilation event, two high-energy gamma photons are emitted in opposite directions. These photon pairs are captured in a detector ring. The occurrence of photon pairs is critical for PET imaging, because the time-of-flight difference, together with the location of the registering detectors, allows us to determine the exact location of the annihilation event in the scanned slice. Moreover, spontaneous background events can be excluded; only coincident gamma pairs are recorded. A sufficient number of recorded events create an image of spatially resolved physiological activity. Like SPECT images, PET images have low spatial resolution and low signal-to-noise ratio.
Visible-Light Imaging Visible-light imaging with conventional digital cameras or specialized scanning elements also play an important role in biomedical imaging. Often, visible-light imaging is found in conjunction with microscopy. A large number of techniques provide information about the imaged object, such as a cell layer or tissue sample. Tissue can be stained (histology) or labeled fluorescently. Fluorescent markers can provide physiological information on the microscopic level in a complementary fashion to SPECT and PET, which provide physiological information on a macroscopic level. Confocal microscopy allows us to obtain three-dimensional volumetric images.